Inference of Causal Effects when Adjustment Sets are Unknown
Paper and Code
Dec 15, 2020
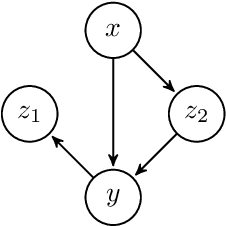

Conventional methods in causal effect inference typically rely on specifying a valid set of adjustment variables. When this set is unknown or misspecified, inferences will be erroneous. We propose a method for inferring average causal effects when the adjustment set is unknown. When the data-generating process belongs to the class of acyclical linear structural equation models, we prove that the method yields asymptotically valid confidence intervals. Our results build upon a smooth characterization of linear acyclic directed graphs. We verify the capability of the method to produce valid confidence intervals for average causal effects using synthetic data, even when the appropriate adjustment sets are unknown.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge