Min-Max Framework for Majorization-Minimization Algorithms in Signal Processing Applications: An Overview

This monograph presents a theoretical background and a broad introduction to the Min-Max Framework for Majorization-Minimization (MM4MM), an algorithmic methodology for solving minimization problems by formulating them as min-max problems and then employing majorization-minimization. The monograph lays out the mathematical basis of the approach used to reformulate a minimization problem as a min-max problem. With the prerequisites covered, including multiple illustrations of the formulations for convex and non-convex functions, this work serves as a guide for developing MM4MM-based algorithms for solving non-convex optimization problems in various areas of signal processing. As special cases, we discuss using the majorization-minimization technique to solve min-max problems encountered in signal processing applications and min-max problems formulated using the Lagrangian. Lastly, we present detailed examples of using MM4MM in ten signal processing applications such as phase retrieval, source localization, independent vector analysis, beamforming and optimal sensor placement in wireless sensor networks. The devised MM4MM algorithms are free of hyper-parameters and enjoy the advantages inherited from the use of the majorization-minimization technique such as monotonicity.

Certified Inventory Control of Critical Resources

Inventory control is subject to service-level requirements, in which sufficient stock levels must be maintained despite an unknown demand. We propose a data-driven order policy that certifies any prescribed service level under minimal assumptions on the unknown demand process. The policy achieves this using any online learning method along with integral action. We further propose an inference method that is valid in finite samples. The properties and theoretical guarantees of the method are illustrated using both synthetic and real-world data.

Two new algorithms for maximum likelihood estimation of sparse covariance matrices with applications to graphical modeling

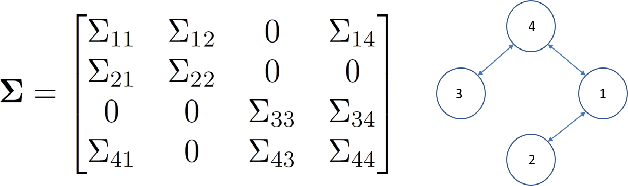
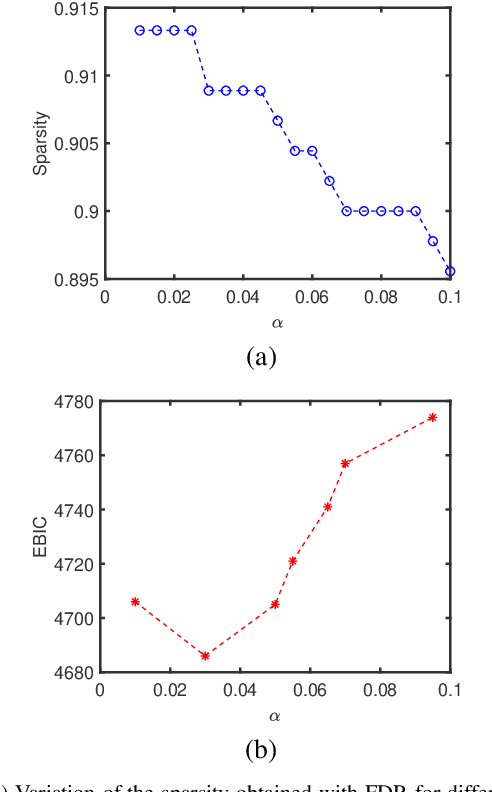
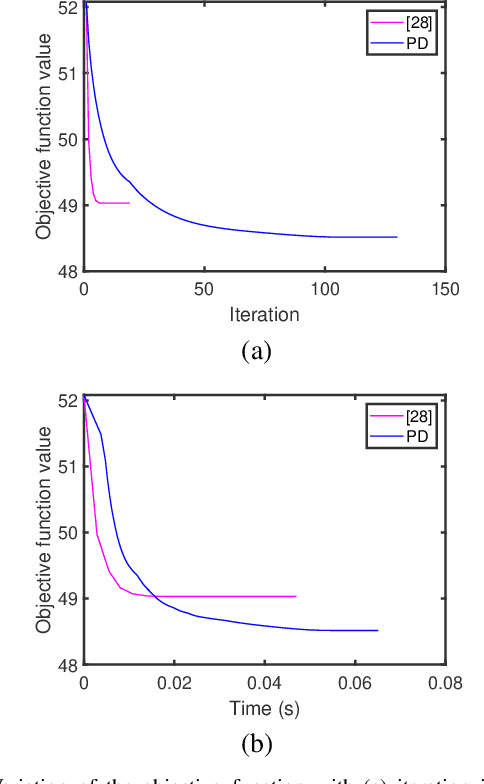
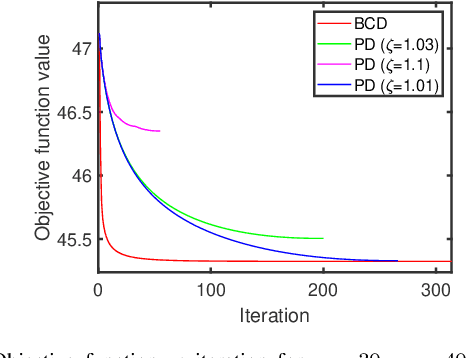
In this paper, we propose two new algorithms for maximum-likelihood estimation (MLE) of high dimensional sparse covariance matrices. Unlike most of the state of-the-art methods, which either use regularization techniques or penalize the likelihood to impose sparsity, we solve the MLE problem based on an estimated covariance graph. More specifically, we propose a two-stage procedure: in the first stage, we determine the sparsity pattern of the target covariance matrix (in other words the marginal independence in the covariance graph under a Gaussian graphical model) using the multiple hypothesis testing method of false discovery rate (FDR), and in the second stage we use either a block coordinate descent approach to estimate the non-zero values or a proximal distance approach that penalizes the distance between the estimated covariance graph and the target covariance matrix. Doing so gives rise to two different methods, each with its own advantage: the coordinate descent approach does not require tuning of any hyper-parameters, whereas the proximal distance approach is computationally fast but requires a careful tuning of the penalty parameter. Both methods are effective even in cases where the number of observed samples is less than the dimension of the data. For performance evaluation, we test the proposed methods on both simulated and real-world data and show that they provide more accurate estimates of the sparse covariance matrix than two state-of-the-art methods.

Pearson-Matthews correlation coefficients for binary and multinary classification and hypothesis testing

The Pearson-Matthews correlation coefficient (usually abbreviated MCC) is considered to be one of the most useful metrics for the performance of a binary classification or hypothesis testing method (for the sake of conciseness we will use the classification terminology throughout, but the concepts and methods discussed in the paper apply verbatim to hypothesis testing as well). For multinary classification tasks (with more than two classes) the existing extension of MCC, commonly called the $\text{R}_{\text{K}}$ metric, has also been successfully used in many applications. The present paper begins with an introductory discussion on certain aspects of MCC. Then we go on to discuss the topic of multinary classification that is the main focus of this paper and which, despite its practical and theoretical importance, appears to be less developed than the topic of binary classification. Our discussion of the $\text{R}_{\text{K}}$ is followed by the introduction of two other metrics for multinary classification derived from the multivariate Pearson correlation (MPC) coefficients. We show that both $\text{R}_{\text{K}}$ and the MPC metrics suffer from the problem of not decisively indicating poor classification results when they should, and introduce three new enhanced metrics that do not suffer from this problem. We also present an additional new metric for multinary classification which can be viewed as a direct extension of MCC.

Fair principal component analysis (PCA): minorization-maximization algorithms for Fair PCA, Fair Robust PCA and Fair Sparse PCA

In this paper we propose a new iterative algorithm to solve the fair PCA (FPCA) problem. We start with the max-min fair PCA formulation originally proposed in [1] and derive a simple and efficient iterative algorithm which is based on the minorization-maximization (MM) approach. The proposed algorithm relies on the relaxation of a semi-orthogonality constraint which is proved to be tight at every iteration of the algorithm. The vanilla version of the proposed algorithm requires solving a semi-definite program (SDP) at every iteration, which can be further simplified to a quadratic program by formulating the dual of the surrogate maximization problem. We also propose two important reformulations of the fair PCA problem: a) fair robust PCA -- which can handle outliers in the data, and b) fair sparse PCA -- which can enforce sparsity on the estimated fair principal components. The proposed algorithms are computationally efficient and monotonically increase their respective design objectives at every iteration. An added feature of the proposed algorithms is that they do not require the selection of any hyperparameter (except for the fair sparse PCA case where a penalty parameter that controls the sparsity has to be chosen by the user). We numerically compare the performance of the proposed methods with two of the state-of-the-art approaches on synthetic data sets and a real-life data set.

Low-rank covariance matrix estimation for factor analysis in anisotropic noise: application to array processing and portfolio selection

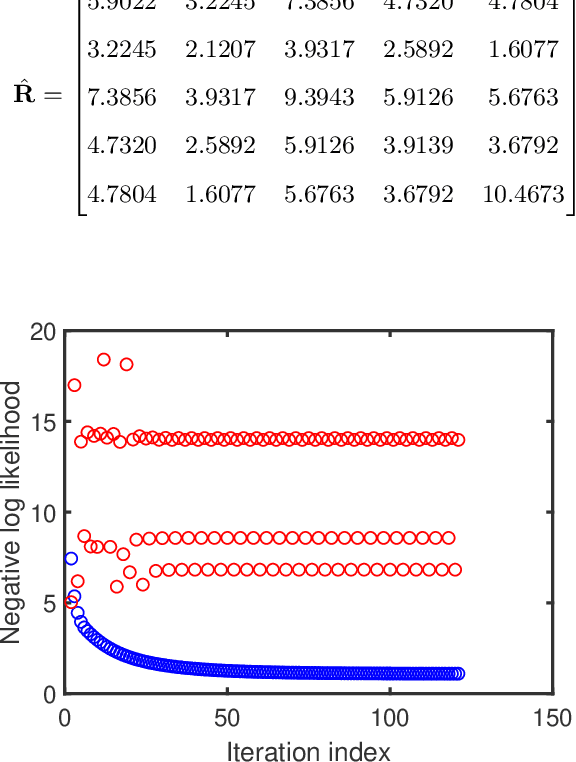
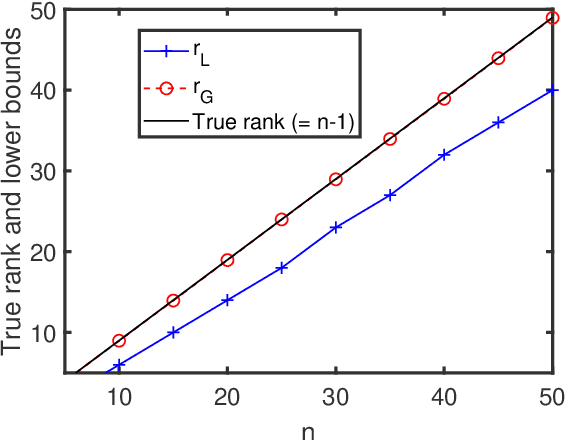
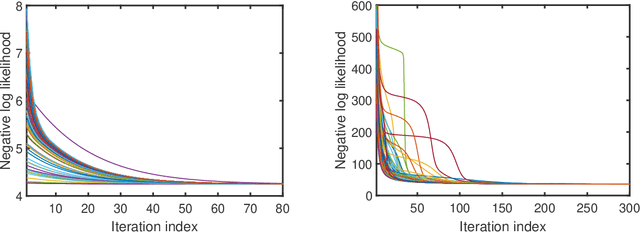
Factor analysis (FA) or principal component analysis (PCA) models the covariance matrix of the observed data as R = SS' + {\Sigma}, where SS' is the low-rank covariance matrix of the factors (aka latent variables) and {\Sigma} is the diagonal matrix of the noise. When the noise is anisotropic (aka nonuniform in the signal processing literature and heteroscedastic in the statistical literature), the diagonal elements of {\Sigma} cannot be assumed to be identical and they must be estimated jointly with the elements of SS'. The problem of estimating SS' and {\Sigma} in the above covariance model is the central theme of the present paper. After stating this problem in a more formal way, we review the main existing algorithms for solving it. We then go on to show that these algorithms have reliability issues (such as lack of convergence or convergence to infeasible solutions) and therefore they may not be the best possible choice for practical applications. Next we explain how to modify one of these algorithms to improve its convergence properties and we also introduce a new method that we call FAAN (Factor Analysis for Anisotropic Noise). FAAN is a coordinate descent algorithm that iteratively maximizes the normal likelihood function, which is easy to implement in a numerically efficient manner and has excellent convergence properties as illustrated by the numerical examples presented in the paper. Out of the many possible applications of FAAN we focus on the following two: direction-of-arrival (DOA) estimation using array signal processing techniques and portfolio selection for financial asset management.

Monte-Carlo Sampling Approach to Model Selection: A Primer

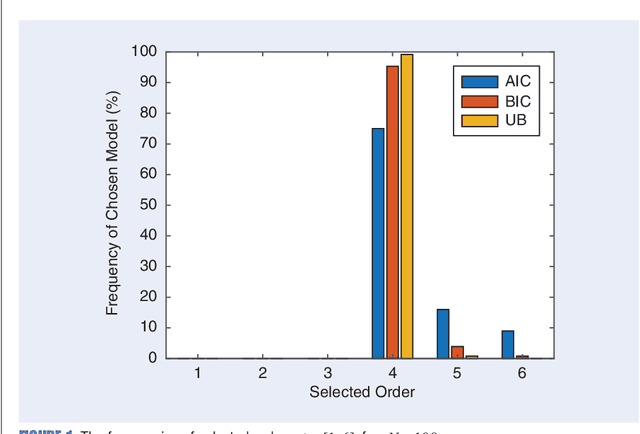
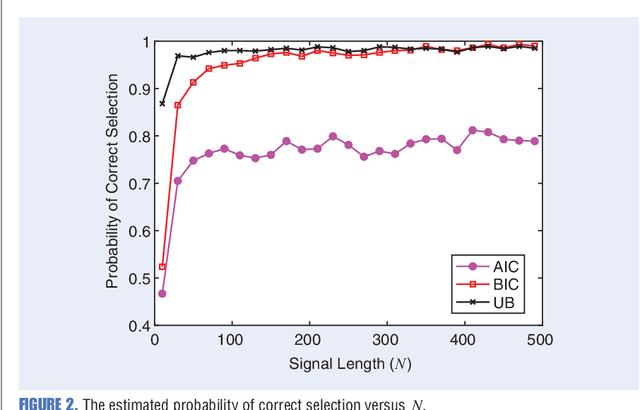
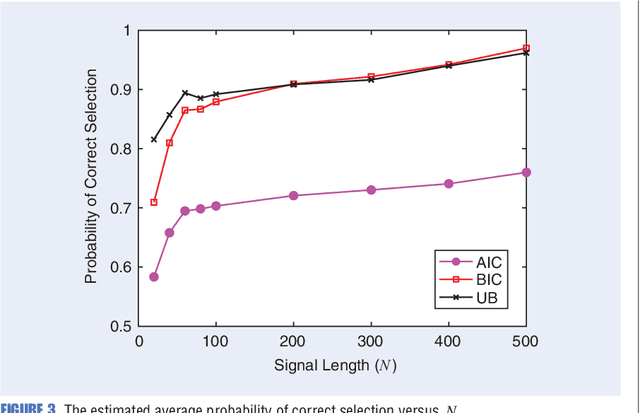
Any data modeling exercise has two main components: parameter estimation and model selection. The latter will be the topic of this lecture note. More concretely we will introduce several Monte-Carlo sampling-based rules for model selection using the maximum a posteriori (MAP) approach. Model selection problems are omnipresent in signal processing applications: examples include selecting the order of an autoregressive predictor, the length of the impulse response of a communication channel, the number of source signals impinging on an array of sensors, the order of a polynomial trend, the number of components of a NMR signal, and so on.

The Cramer-Rao Bound for Signal Parameter Estimation from Quantized Data

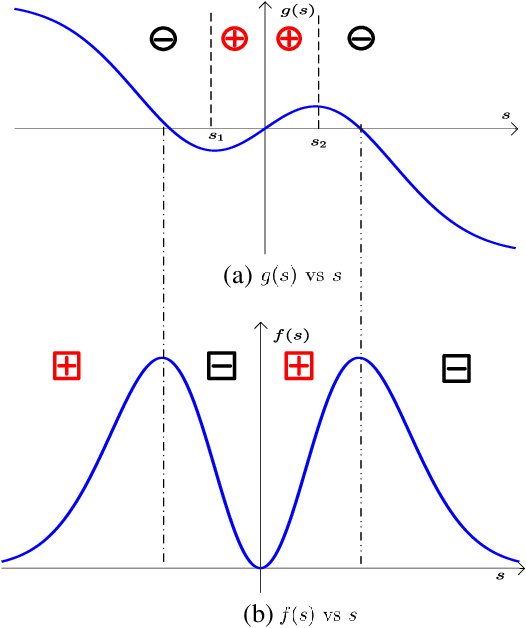
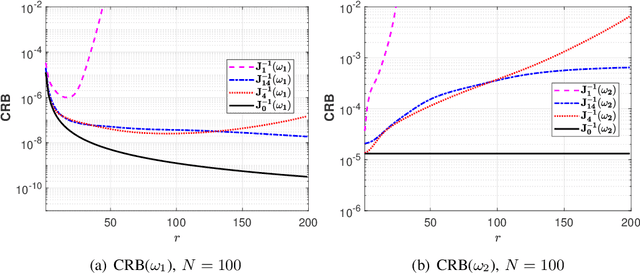
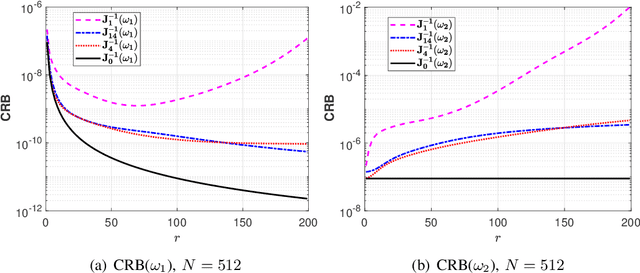
Several current ultra-wide band applications, such as millimeter wave radar and communication systems, require high sampling rates and therefore expensive and energy-hungry analogto-digital converters (ADCs). In applications where cost and power constraints exist, the use of high-precision ADCs is not feasible and the designer must resort to ADCs with coarse quantization. Consequently the interest in the topic of signal parameter estimation from quantized data has increased significantly in recent years. The Cramer-Rao bound (CRB) is an important yardstick in any parameter estimation problem. Indeed it lower bounds the variance of any unbiased parameter estimator. Moreover, the CRB is an achievable limit, for instance it is asymptotically attained by the maximum likelihood estimator (under regularity conditions), and thus it is a useful benchmark to which the accuracy of any parameter estimator can and should be compared. A formula for the CRB for signal parameter estimation from real-valued quantized data has been presented in but its derivation was somewhat sketchy. The said CRB formula has been extended for instance in to complex-valued quantized data, but again its derivation was rather sketchy. The special case of binary (1-bit) ADCs and a signal consisting of one sinusoid has been thoroughly analyzed in . The CRB formula for a binary ADC and a general real-valued signal has been derived.

MIMO Multifunction RF Systems: Detection Performance and Waveform Design

This paper studies the detection performance of a multiple-input-multiple-output (MIMO) multifunction radio frequency (MFRF) system, which simultaneously supports radar, communication, and jamming. We show that the detection performance of the MIMO MFRF system improves as the transmit signal-to-interference-plus-noise-ratio (SINR) increases. To analyze the achievable SINR of the system, we formulate an SINR maximization problem under the communication and jamming functionality constraint as well as a transmit energy constraint. We derive a closed-form solution of this optimization problem for energy-constrained waveforms and present a detailed analysis of the achievable SINR. Moreover, we analyze the SINR for systems transmitting constant-modulus waveforms, which are often used in practice. We propose an efficient constant-modulus waveform design algorithm to maximize the SINR. Numerical results demonstrate the capability of a MIMO array to provide multiple functions, and also show the tradeoff between radar detection and the communication/jamming functionality.

Diagnostic Tool for Out-of-Sample Model Evaluation

Assessment of model fitness is an important step in many problems. Models are typically fitted to training data by minimizing a loss function, such as the squared-error or negative log-likelihood, and it is natural to desire low losses on future data. This letter considers the use of a test data set to characterize the out-of-sample losses of a model. We propose a simple model diagnostic tool that provides finite-sample guarantees under weak assumptions. The tool is computationally efficient and can be interpreted as an empirical quantile. Several numerical experiments are presented to show how the proposed method quantifies the impact of distribution shifts, aids the analysis of regression, and enables model selection as well as hyper-parameter tuning.