CRB Analysis for Mixed-ADC Based DOA Estimation

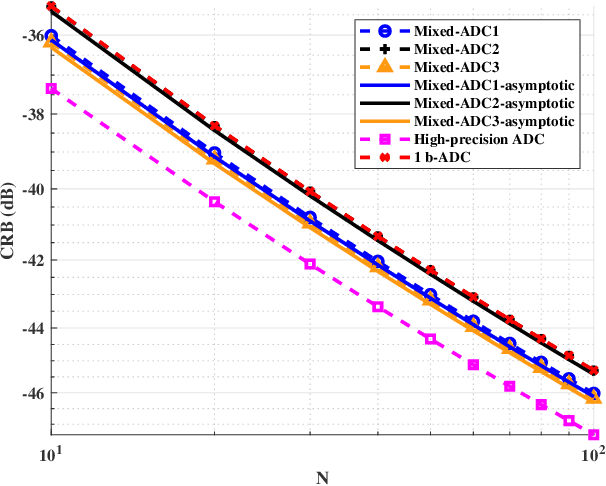
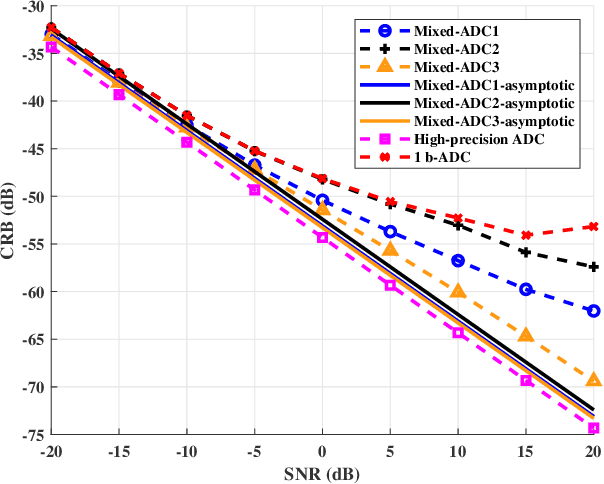
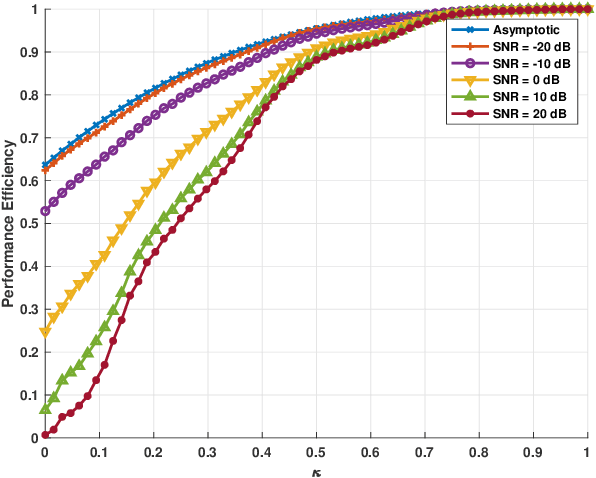
We consider a mixed analog-to-digital converter (ADC) based architecture consisting of high-precision and one-bit ADCs with the antenna-varying threshold for direction of arrival (DOA) estimation using a uniform linear array (ULA), which utilizes fixed but different thresholds for one-bit ADCs across different receive antennas. The Cram{\'e}r-Rao bound (CRB) with the antenna-varying threshold is obtained. Then based on the lower bound of the CRB, we derive the asymptotic CRB of the DOA, which depends on the placement of mixed-ADC. Our analysis shows that distributing high-precision ADCs evenly around the two edges of the ULA yields improved performance. This result can be extended to a more general case where the ULA is equipped with two types of ADCs with different quantization precisions. To efficiently obtain the maximum likelihood DOA estimates, we propose a two-step algorithm. Firstly, we formulate the model as a sparse signal representation problem, and modify the sparse learning via iterative minimization (SLIM) approach to the mixed-ADC based DOA estimation. In the second step, we use the relaxation-based approach to cyclically refine the estimates of SLIM, further enhancing the DOA estimation performance. Numerical examples are presented to demonstrate the validity of the CRB analysis and the effectiveness of our methods.

Mixed-ADC Based PMCW MIMO Radar Angle-Doppler Imaging

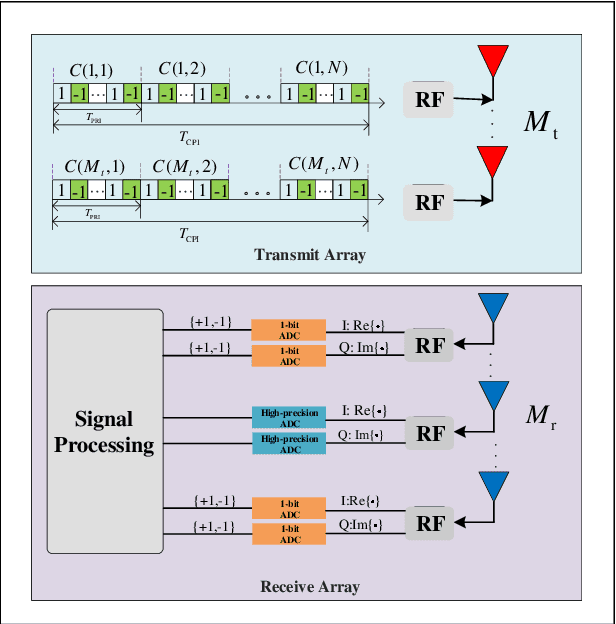
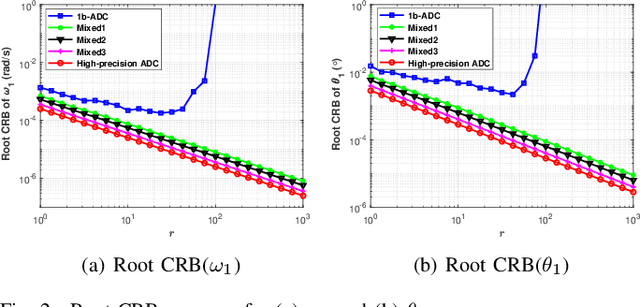
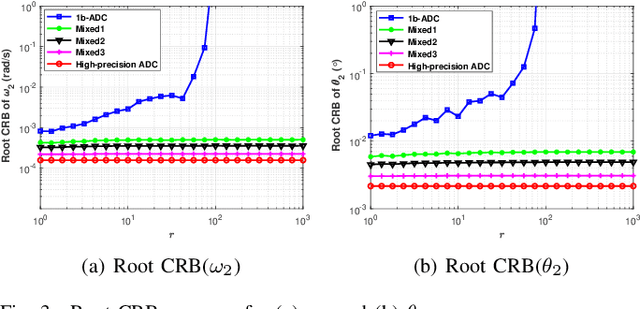
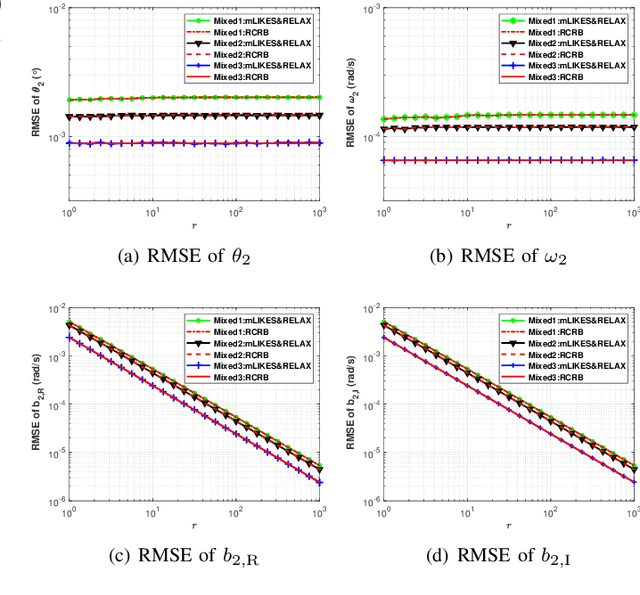
Phase-modulated continuous-wave (PMCW) multiple-input multiple-output (MIMO) radar systems are known to possess excellent mutual interference mitigation capabilities, but require costly and power-hungry high sampling rate and high-precision analog-to-digital converters (ADC's). To reduce cost and power consumption, we consider a mixed-ADC architecture, in which most receive antenna outputs are sampled by one-bit ADC's, and only one or a few outputs by high-precision ADC's. We first derive the Cram{\'e}r-Rao bound (CRB) for the mixed-ADC based PMCW MIMO radar to characterize the best achievable performance of an unbiased target parameter estimator. The CRB analysis demonstrates that the mixed-ADC architecture with a relatively small number of high-precision ADC's and a large number of one-bit ADC's allows us to drastically reduce the hardware cost and power consumption while still maintain a high dynamic range needed for autonomous driving applications. We also introduce a two-step estimator to realize the computationally efficient maximum likelihood (ML) estimation of the target parameters. We formulate the angle-Doppler imaging problem as a sparse parameter estimation problem, and a computationally efficient majorization-minimization (MM) based estimator of sparse parameters, referred to as mLIKES, is devised for accurate angle-Doppler imaging. This is followed by using a relaxation-based approach to cyclically refine the results of mLIKES for accurate off-grid target parameter estimation. Numerical examples are provided to demonstrate the effectiveness of the proposed algorithms for angle-Doppler imaging using mixed-ADC based PMCW MIMO radar.

Code Optimization and Angle-Doppler Imaging for ST-CDM LFMCW MIMO Radar Systems

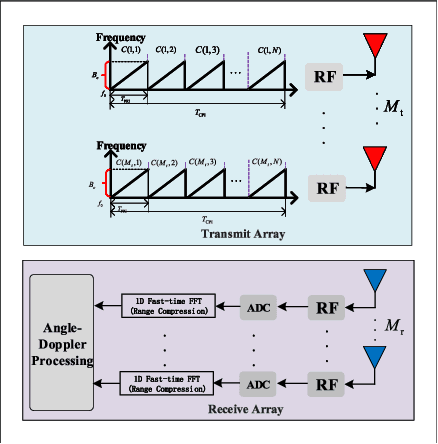
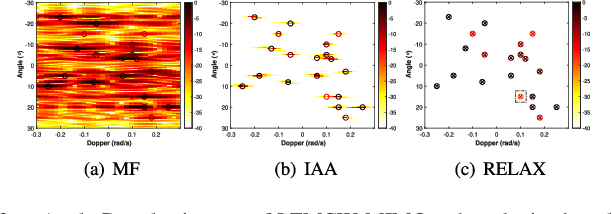
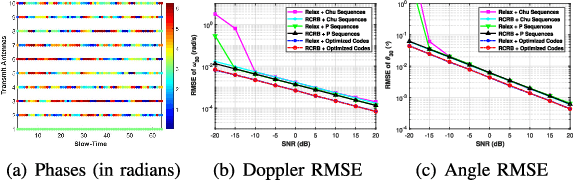
We consider code optimization and angle-Doppler imaging for slow-time code division multiplexing (ST-CDM) linear frequency-modulated continuous-wave (LFMCW) multiple-input multiple-output (MIMO) radar systems. We optimize the slow-time code via the minimization of a Cram{\'e}r-Rao Bound (CRB)-based metric to enhance the parameter estimation performance. Then, a computationally efficient RELAX-based algorithm is presented to obtain the maximum likelihood (ML) estimates of the target angle-Doppler parameters. Numerical examples show that the proposed approaches can be used to improve the performance of parameter estimation and angle-Doppler imaging of ST-CDM LFMCW MIMO radar systems.

Optimal Mixed-ADC arrangement for DOA Estimation via CRB using ULA

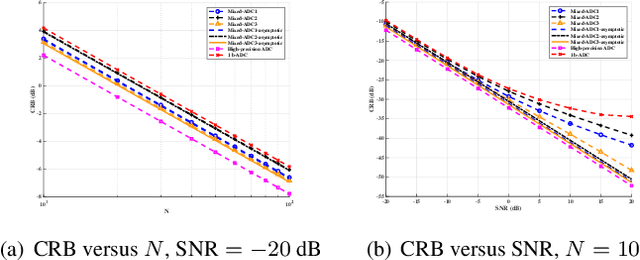
We consider a mixed analog-to-digital converter (ADC) based architecture for direction of arrival (DOA) estimation using a uniform linear array (ULA). We derive the Cram{\'e}r-Rao bound (CRB) of the DOA under the optimal time-varying threshold, and find that the asymptotic CRB is related to the arrangement of high-precision and one-bit ADCs for a fixed number of ADCs. Then, a new concept called ``mixed-precision arrangement" is proposed. It is proven that better performance for DOA estimation is achieved when high-precision ADCs are distributed evenly around the edges of the ULA. This result can be extended to a more general case where the ULA is equipped with various precision ADCs. Simulation results show the validity of the asymptotic CRB and better performance under the optimal mixed-precision arrangement.

Monte-Carlo Sampling Approach to Model Selection: A Primer

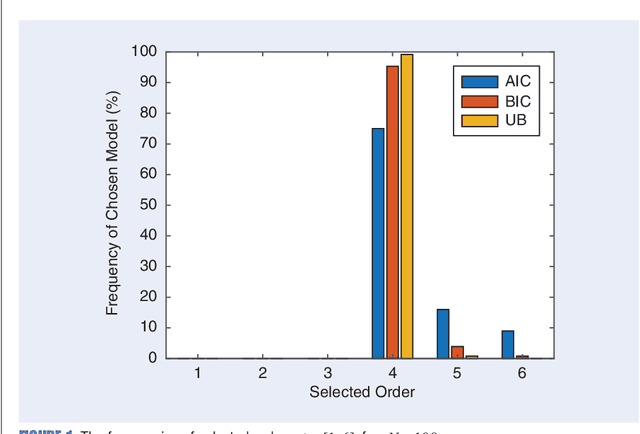
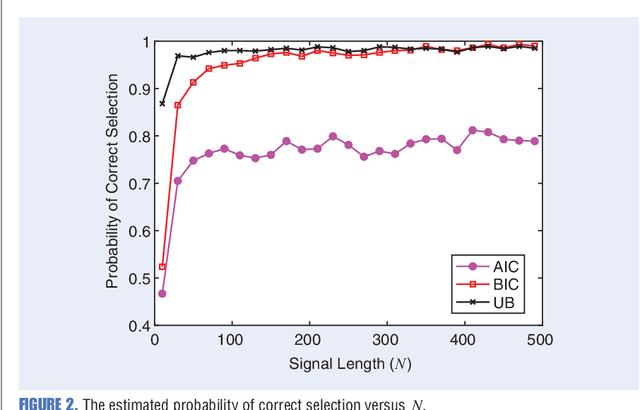
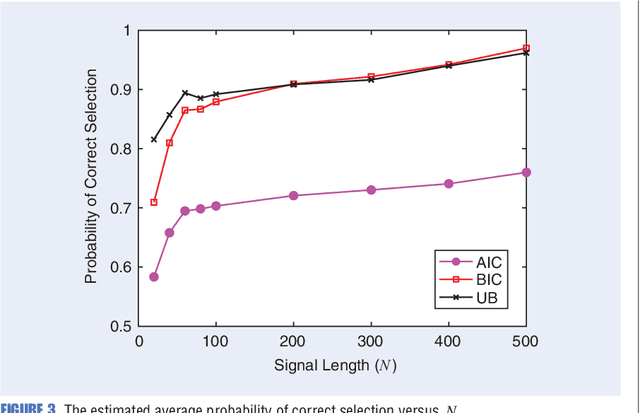
Any data modeling exercise has two main components: parameter estimation and model selection. The latter will be the topic of this lecture note. More concretely we will introduce several Monte-Carlo sampling-based rules for model selection using the maximum a posteriori (MAP) approach. Model selection problems are omnipresent in signal processing applications: examples include selecting the order of an autoregressive predictor, the length of the impulse response of a communication channel, the number of source signals impinging on an array of sensors, the order of a polynomial trend, the number of components of a NMR signal, and so on.

The Cramer-Rao Bound for Signal Parameter Estimation from Quantized Data

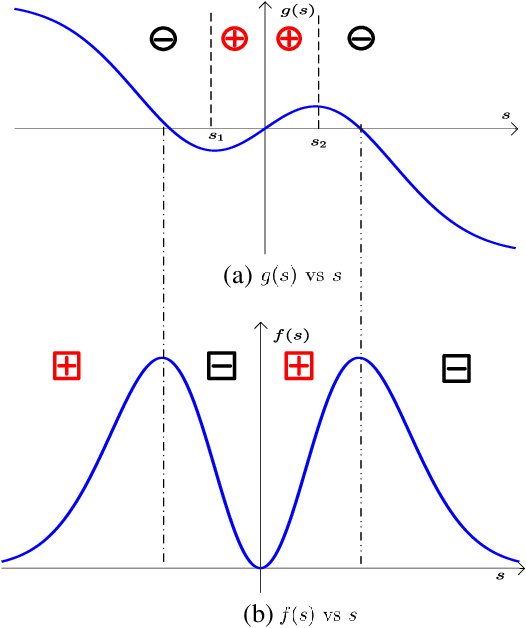
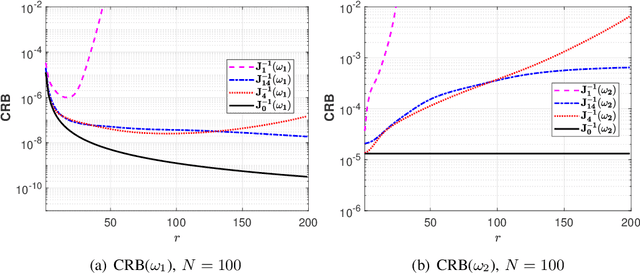
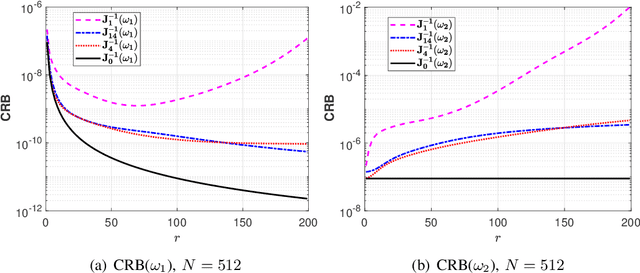
Several current ultra-wide band applications, such as millimeter wave radar and communication systems, require high sampling rates and therefore expensive and energy-hungry analogto-digital converters (ADCs). In applications where cost and power constraints exist, the use of high-precision ADCs is not feasible and the designer must resort to ADCs with coarse quantization. Consequently the interest in the topic of signal parameter estimation from quantized data has increased significantly in recent years. The Cramer-Rao bound (CRB) is an important yardstick in any parameter estimation problem. Indeed it lower bounds the variance of any unbiased parameter estimator. Moreover, the CRB is an achievable limit, for instance it is asymptotically attained by the maximum likelihood estimator (under regularity conditions), and thus it is a useful benchmark to which the accuracy of any parameter estimator can and should be compared. A formula for the CRB for signal parameter estimation from real-valued quantized data has been presented in but its derivation was somewhat sketchy. The said CRB formula has been extended for instance in to complex-valued quantized data, but again its derivation was rather sketchy. The special case of binary (1-bit) ADCs and a signal consisting of one sinusoid has been thoroughly analyzed in . The CRB formula for a binary ADC and a general real-valued signal has been derived.

Weighted SPICE Algorithms for Range-Doppler Imaging Using One-Bit Automotive Radar

We consider the problem of range-Doppler imaging using one-bit automotive LFMCW1 or PMCW radar that utilizes one-bit ADC sampling with time-varying thresholds at the receiver. The one-bit sampling technique can significantly reduce the cost as well as the power consumption of automotive radar systems. We formulate the one-bit LFMCW/PMCW radar rangeDoppler imaging problem as one-bit sparse parameter estimation. The recently proposed hyperparameter-free (and hence user friendly) weighted SPICE algorithms, including SPICE, LIKES, SLIM and IAA, achieve excellent parameter estimation performance for data sampled with high precision. However, these algorithms cannot be used directly for one-bit data. In this paper we first present a regularized minimization algorithm, referred to as 1bSLIM, for accurate range-Doppler imaging using onebit radar systems. Then, we describe how to extend the SPICE, LIKES and IAA algorithms to the one-bit data case, and refer to these extensions as 1bSPICE, 1bLIKES and 1bIAA. These onebit hyperparameter-free algorithms are unified within the one-bit weighted SPICE framework. Moreover, efficient implementations of the aforementioned algorithms are investigated that rely heavily on the use of FFTs. Finally, both simulated and experimental examples are provided to demonstrate the effectiveness of the proposed algorithms for range-Doppler imaging using one-bit automotive radar systems.