CRB Analysis for Mixed-ADC Based DOA Estimation
Paper and Code
Mar 14, 2024
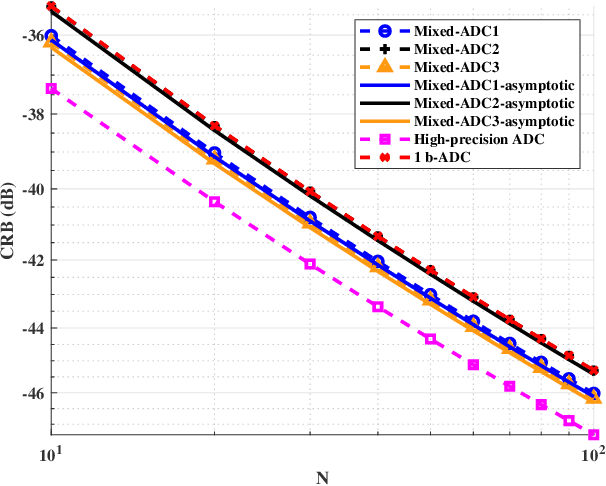
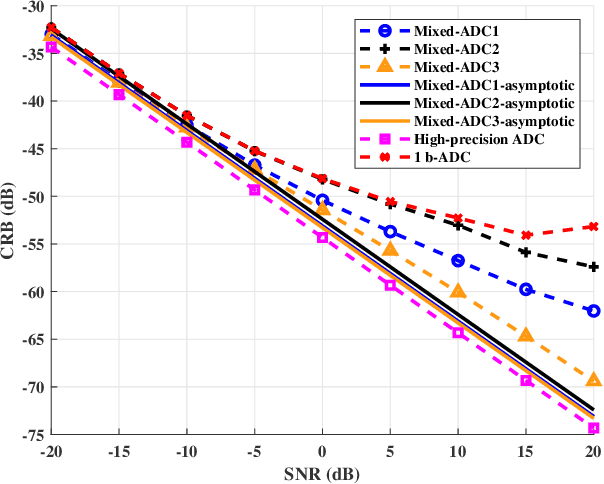
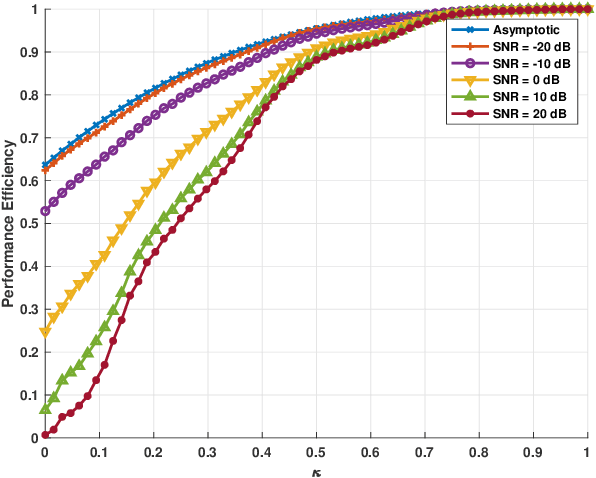
We consider a mixed analog-to-digital converter (ADC) based architecture consisting of high-precision and one-bit ADCs with the antenna-varying threshold for direction of arrival (DOA) estimation using a uniform linear array (ULA), which utilizes fixed but different thresholds for one-bit ADCs across different receive antennas. The Cram{\'e}r-Rao bound (CRB) with the antenna-varying threshold is obtained. Then based on the lower bound of the CRB, we derive the asymptotic CRB of the DOA, which depends on the placement of mixed-ADC. Our analysis shows that distributing high-precision ADCs evenly around the two edges of the ULA yields improved performance. This result can be extended to a more general case where the ULA is equipped with two types of ADCs with different quantization precisions. To efficiently obtain the maximum likelihood DOA estimates, we propose a two-step algorithm. Firstly, we formulate the model as a sparse signal representation problem, and modify the sparse learning via iterative minimization (SLIM) approach to the mixed-ADC based DOA estimation. In the second step, we use the relaxation-based approach to cyclically refine the estimates of SLIM, further enhancing the DOA estimation performance. Numerical examples are presented to demonstrate the validity of the CRB analysis and the effectiveness of our methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge