The Cramer-Rao Bound for Signal Parameter Estimation from Quantized Data
Paper and Code
Sep 27, 2022
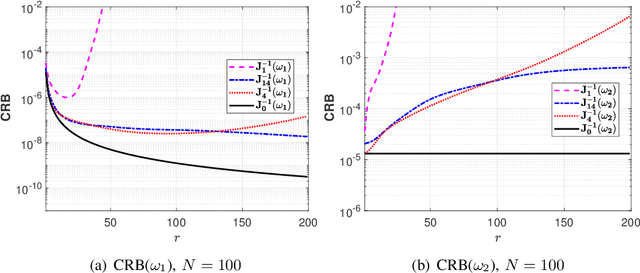
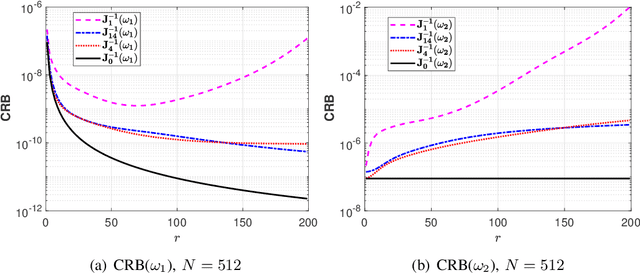
Several current ultra-wide band applications, such as millimeter wave radar and communication systems, require high sampling rates and therefore expensive and energy-hungry analogto-digital converters (ADCs). In applications where cost and power constraints exist, the use of high-precision ADCs is not feasible and the designer must resort to ADCs with coarse quantization. Consequently the interest in the topic of signal parameter estimation from quantized data has increased significantly in recent years. The Cramer-Rao bound (CRB) is an important yardstick in any parameter estimation problem. Indeed it lower bounds the variance of any unbiased parameter estimator. Moreover, the CRB is an achievable limit, for instance it is asymptotically attained by the maximum likelihood estimator (under regularity conditions), and thus it is a useful benchmark to which the accuracy of any parameter estimator can and should be compared. A formula for the CRB for signal parameter estimation from real-valued quantized data has been presented in but its derivation was somewhat sketchy. The said CRB formula has been extended for instance in to complex-valued quantized data, but again its derivation was rather sketchy. The special case of binary (1-bit) ADCs and a signal consisting of one sinusoid has been thoroughly analyzed in . The CRB formula for a binary ADC and a general real-valued signal has been derived.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge