New Methods for MLE of Toeplitz Structured Covariance Matrices with Applications to RADAR Problems

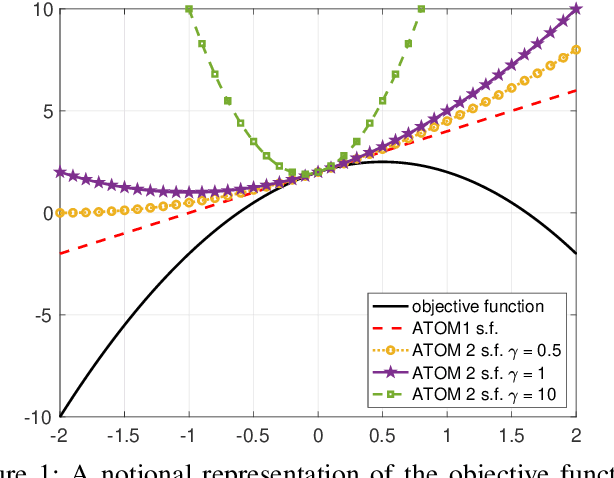
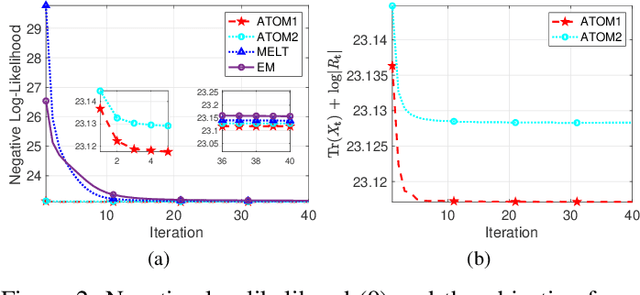
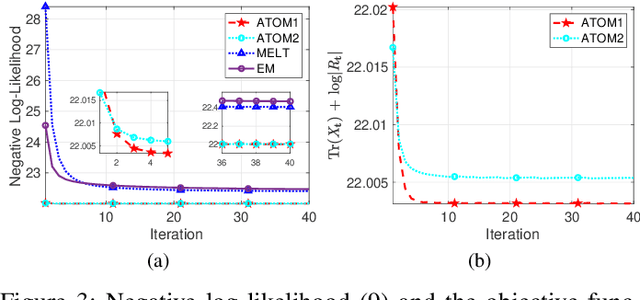
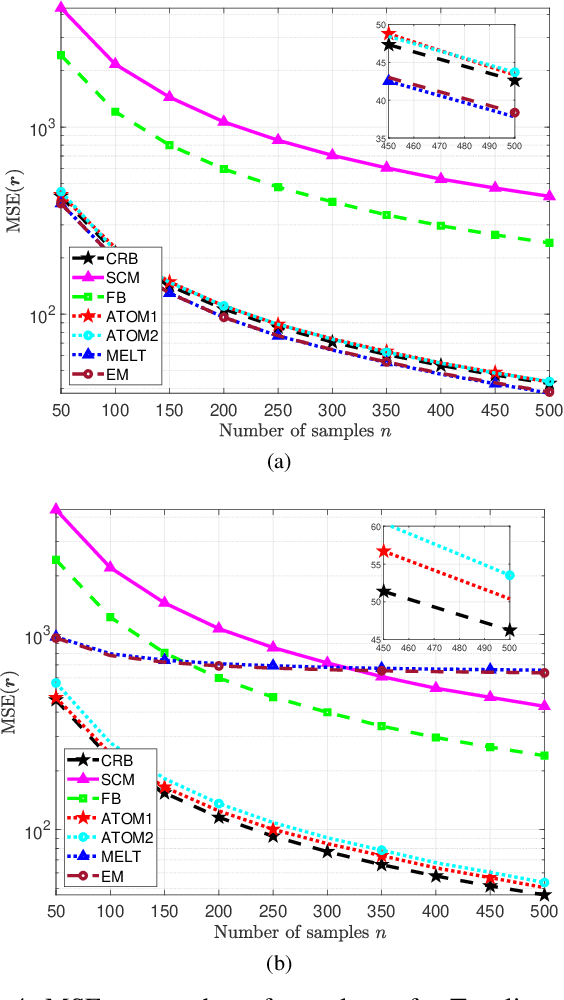
This work considers Maximum Likelihood Estimation (MLE) of a Toeplitz structured covariance matrix. In this regard, an equivalent reformulation of the MLE problem is introduced and two iterative algorithms are proposed for the optimization of the equivalent statistical learning framework. Both the strategies are based on the Majorization Minimization (MM) paradigm and hence enjoy nice properties such as monotonicity and ensured convergence to a stationary point of the equivalent MLE problem. The proposed framework is also extended to deal with MLE of other practically relevant covariance structures, namely, the banded Toeplitz, block Toeplitz, and Toeplitz-block-Toeplitz. Through numerical simulations, it is shown that the new methods provide excellent performance levels in terms of both mean square estimation error (which is very close to the benchmark Cram\'er-Rao Bound (CRB)) and signal-to-interference-plus-noise ratio, especially in comparison with state of the art strategies.

Two new algorithms for maximum likelihood estimation of sparse covariance matrices with applications to graphical modeling

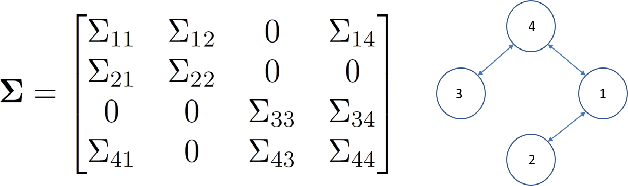
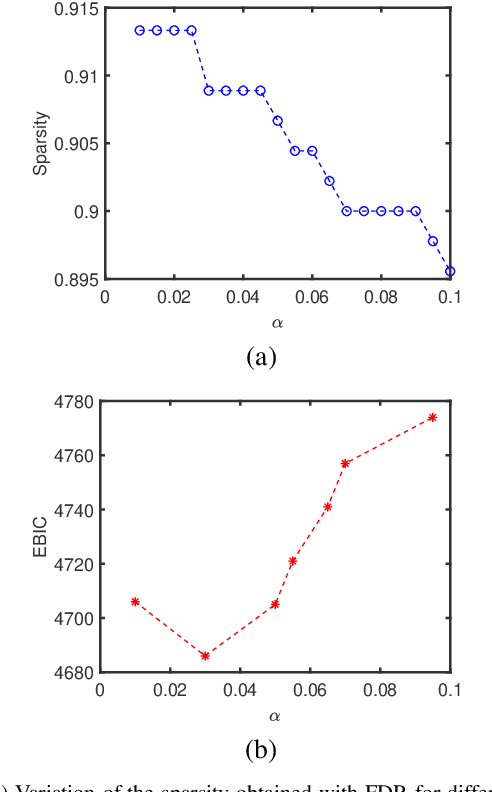
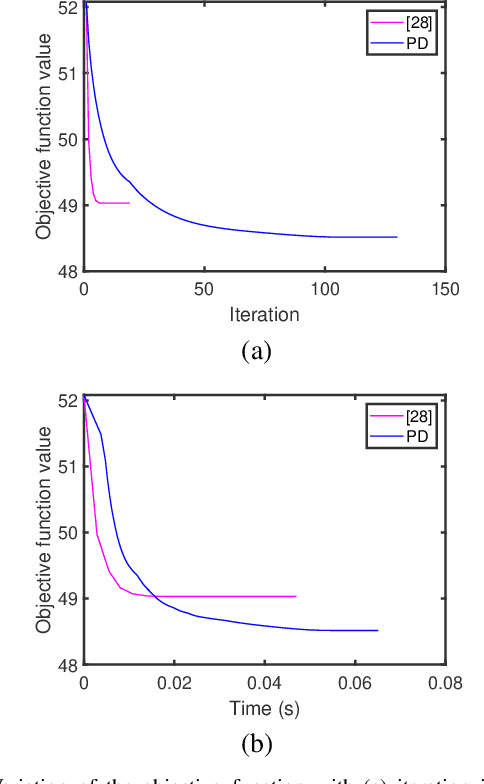
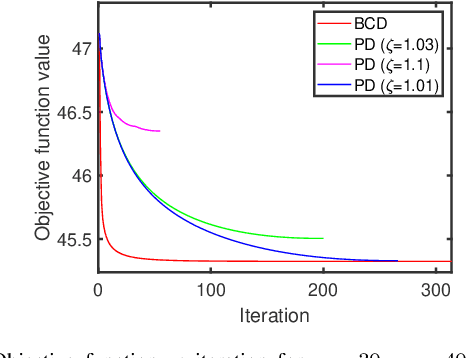
In this paper, we propose two new algorithms for maximum-likelihood estimation (MLE) of high dimensional sparse covariance matrices. Unlike most of the state of-the-art methods, which either use regularization techniques or penalize the likelihood to impose sparsity, we solve the MLE problem based on an estimated covariance graph. More specifically, we propose a two-stage procedure: in the first stage, we determine the sparsity pattern of the target covariance matrix (in other words the marginal independence in the covariance graph under a Gaussian graphical model) using the multiple hypothesis testing method of false discovery rate (FDR), and in the second stage we use either a block coordinate descent approach to estimate the non-zero values or a proximal distance approach that penalizes the distance between the estimated covariance graph and the target covariance matrix. Doing so gives rise to two different methods, each with its own advantage: the coordinate descent approach does not require tuning of any hyper-parameters, whereas the proximal distance approach is computationally fast but requires a careful tuning of the penalty parameter. Both methods are effective even in cases where the number of observed samples is less than the dimension of the data. For performance evaluation, we test the proposed methods on both simulated and real-world data and show that they provide more accurate estimates of the sparse covariance matrix than two state-of-the-art methods.

Pearson-Matthews correlation coefficients for binary and multinary classification and hypothesis testing

The Pearson-Matthews correlation coefficient (usually abbreviated MCC) is considered to be one of the most useful metrics for the performance of a binary classification or hypothesis testing method (for the sake of conciseness we will use the classification terminology throughout, but the concepts and methods discussed in the paper apply verbatim to hypothesis testing as well). For multinary classification tasks (with more than two classes) the existing extension of MCC, commonly called the $\text{R}_{\text{K}}$ metric, has also been successfully used in many applications. The present paper begins with an introductory discussion on certain aspects of MCC. Then we go on to discuss the topic of multinary classification that is the main focus of this paper and which, despite its practical and theoretical importance, appears to be less developed than the topic of binary classification. Our discussion of the $\text{R}_{\text{K}}$ is followed by the introduction of two other metrics for multinary classification derived from the multivariate Pearson correlation (MPC) coefficients. We show that both $\text{R}_{\text{K}}$ and the MPC metrics suffer from the problem of not decisively indicating poor classification results when they should, and introduce three new enhanced metrics that do not suffer from this problem. We also present an additional new metric for multinary classification which can be viewed as a direct extension of MCC.

Fair principal component analysis (PCA): minorization-maximization algorithms for Fair PCA, Fair Robust PCA and Fair Sparse PCA

In this paper we propose a new iterative algorithm to solve the fair PCA (FPCA) problem. We start with the max-min fair PCA formulation originally proposed in [1] and derive a simple and efficient iterative algorithm which is based on the minorization-maximization (MM) approach. The proposed algorithm relies on the relaxation of a semi-orthogonality constraint which is proved to be tight at every iteration of the algorithm. The vanilla version of the proposed algorithm requires solving a semi-definite program (SDP) at every iteration, which can be further simplified to a quadratic program by formulating the dual of the surrogate maximization problem. We also propose two important reformulations of the fair PCA problem: a) fair robust PCA -- which can handle outliers in the data, and b) fair sparse PCA -- which can enforce sparsity on the estimated fair principal components. The proposed algorithms are computationally efficient and monotonically increase their respective design objectives at every iteration. An added feature of the proposed algorithms is that they do not require the selection of any hyperparameter (except for the fair sparse PCA case where a penalty parameter that controls the sparsity has to be chosen by the user). We numerically compare the performance of the proposed methods with two of the state-of-the-art approaches on synthetic data sets and a real-life data set.

Low-rank covariance matrix estimation for factor analysis in anisotropic noise: application to array processing and portfolio selection

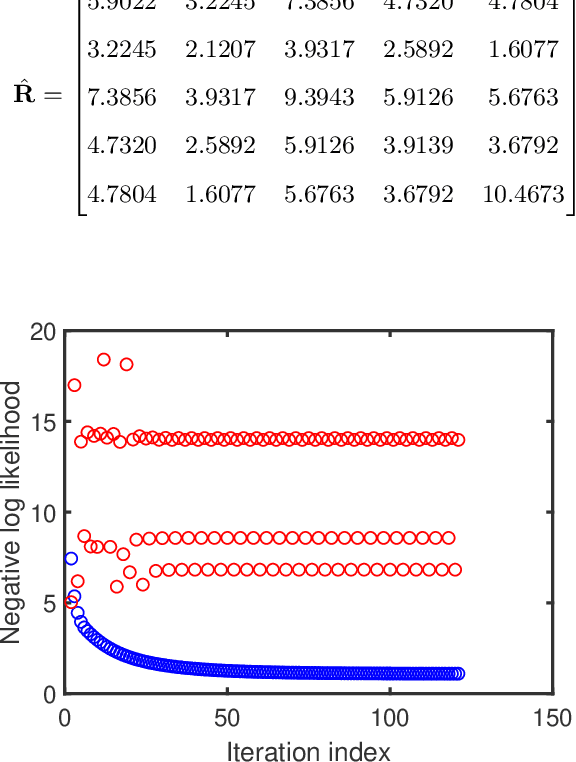
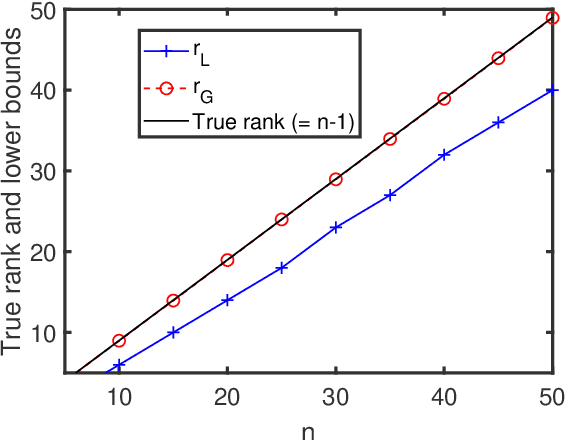
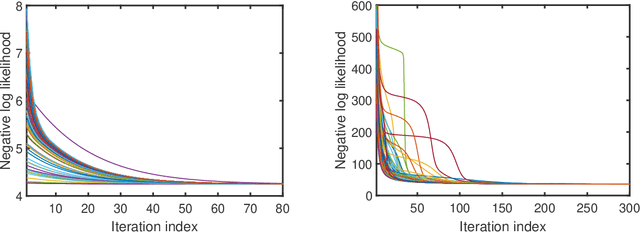
Factor analysis (FA) or principal component analysis (PCA) models the covariance matrix of the observed data as R = SS' + {\Sigma}, where SS' is the low-rank covariance matrix of the factors (aka latent variables) and {\Sigma} is the diagonal matrix of the noise. When the noise is anisotropic (aka nonuniform in the signal processing literature and heteroscedastic in the statistical literature), the diagonal elements of {\Sigma} cannot be assumed to be identical and they must be estimated jointly with the elements of SS'. The problem of estimating SS' and {\Sigma} in the above covariance model is the central theme of the present paper. After stating this problem in a more formal way, we review the main existing algorithms for solving it. We then go on to show that these algorithms have reliability issues (such as lack of convergence or convergence to infeasible solutions) and therefore they may not be the best possible choice for practical applications. Next we explain how to modify one of these algorithms to improve its convergence properties and we also introduce a new method that we call FAAN (Factor Analysis for Anisotropic Noise). FAAN is a coordinate descent algorithm that iteratively maximizes the normal likelihood function, which is easy to implement in a numerically efficient manner and has excellent convergence properties as illustrated by the numerical examples presented in the paper. Out of the many possible applications of FAAN we focus on the following two: direction-of-arrival (DOA) estimation using array signal processing techniques and portfolio selection for financial asset management.

Comments on "Iteratively Re-weighted Algorithm for Fuzzy c-Means"

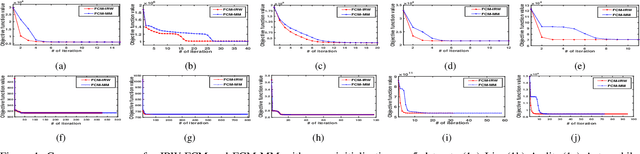
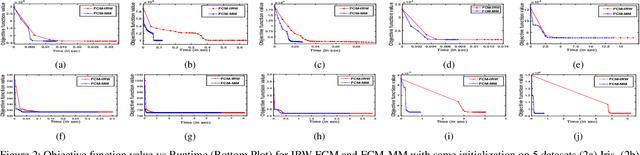
In this comment, we present a simple alternate derivation to the IRW-FCM algorithm presented in "Iteratively Re-weighted Algorithm for Fuzzy c-Means" for Fuzzy c-Means problem. We show that the iterative steps derived for IRW-FCM algorithm are nothing but steps of the popular Majorization Minimization (MM) algorithm. The derivation presented in this note is much simpler and straightforward and, unlike the derivation of IRW-FCM, the derivation here does not involve introduction of any auxiliary variable. Moreover, by showing the steps of IRW-FCM as the MM algorithm, the inner loop of the IRW-FCM algorithm can be eliminated and the algorithm can be effectively run as a "single loop" algorithm. More precisely, the new MM-based derivation deduces that a single inner loop of IRW-FCM is sufficient to decrease the Fuzzy c-means objective function, which speeds up the IRW-FCM algorithm.

Majorization-Minimization based Hybrid Localization Method for High Precision Localization in Wireless Sensor Networks

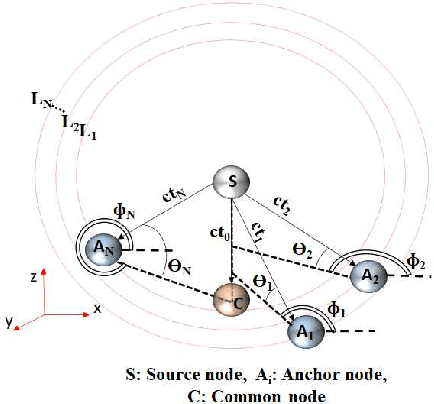
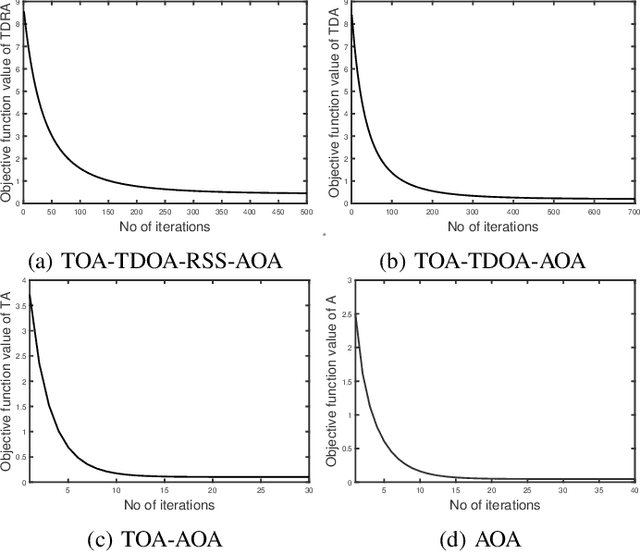
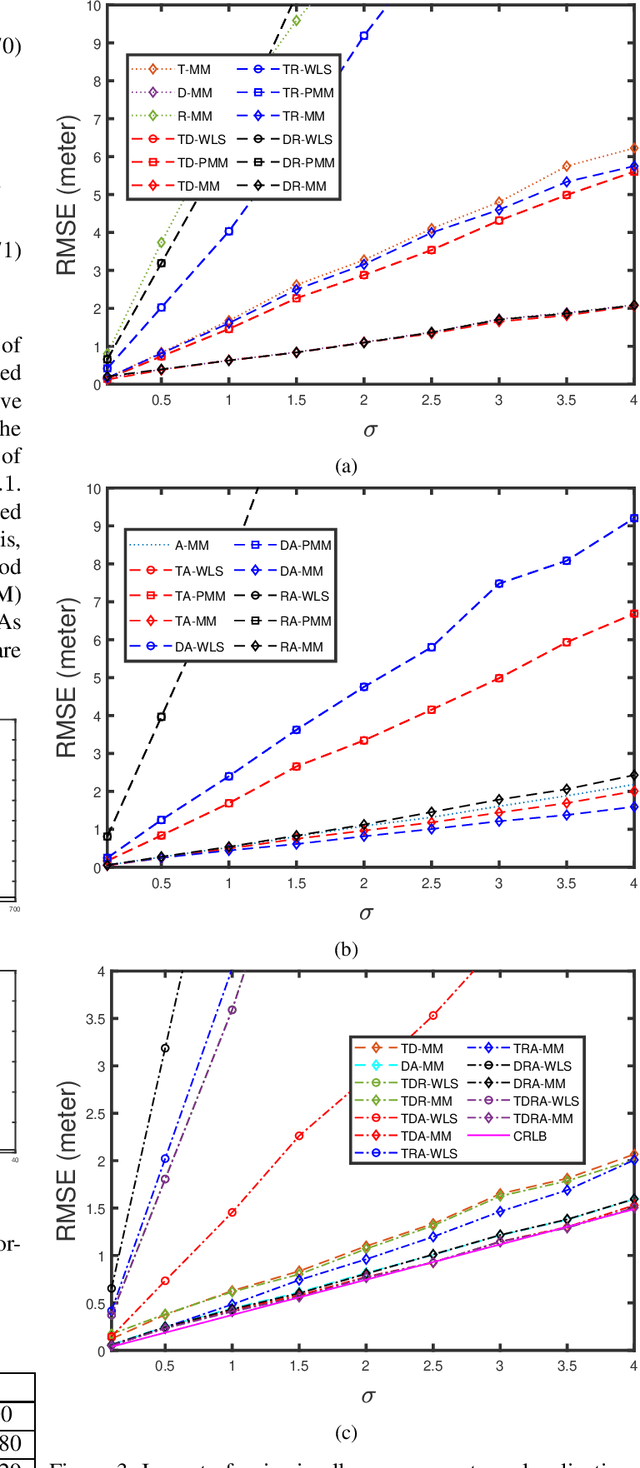
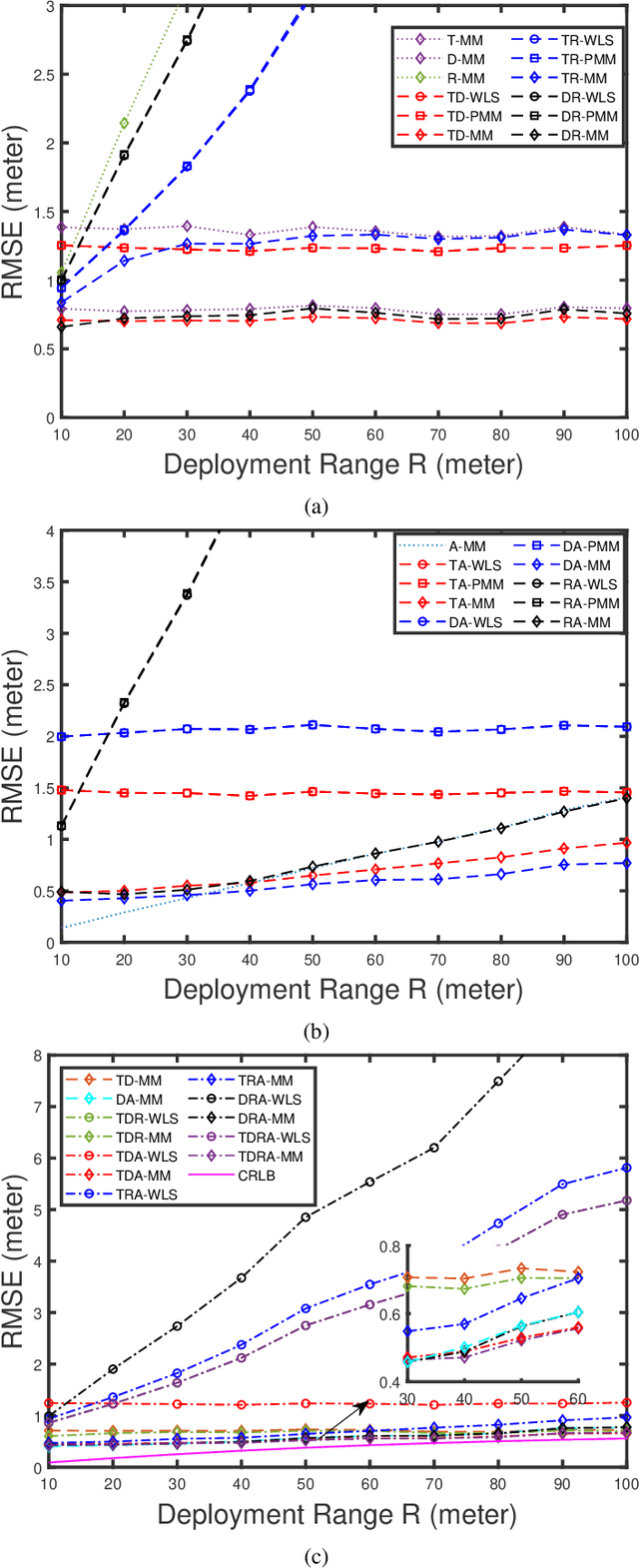
This paper investigates the hybrid source localization problem using the four radio measurements - time of arrival (TOA), time difference of arrival (TDOA), received signal strength (RSS) and angle of arrival (AOA). First, after invoking tractable approximations in the RSS and AOA models, the maximum likelihood estimation (MLE) problem for the hybrid TOA-TDOA-RSS-AOA data model is derived. Then, in the MLE, which has the least-squares objective, weights determined using the range-based characteristics of the four heterogeneous measurements, are introduced. The resultant weighted least-squares problem obtained, which is non-smooth and non-convex, is solved using the principle of the majorization-minimization (MM), leading to an iterative algorithm that has a guaranteed convergence. The key feature of the proposed method is that it provides a unified framework where localization using any possible merger out of these four measurements can be implemented as per the requirement/application. Extensive numerical simulations are conducted to study the estimation efficiency of the proposed method. The proposed method employing all four measurements is compared against a conventionally used method and also against the proposed method employing only limited combinations of the four measurements. The results obtained indicate that the hybrid localization model improves the localization accuracy compared to the heterogeneous measurements. The integration of different measurements also yields good accuracy in the presence of non-line of sight (NLOS) errors.

Optimal Sensor Placement for Hybrid Source Localization Using Fused TOA-RSS-AOA Measurements

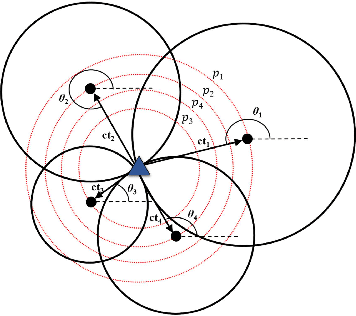
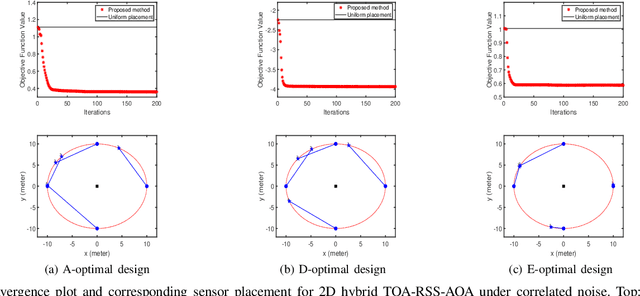
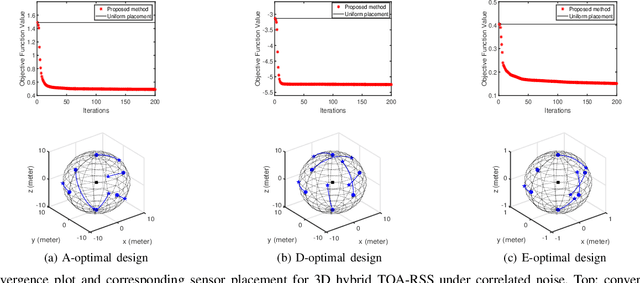
Source localization techniques incorporating hybrid measurements improve the reliability and accuracy of the location estimate. Given a set of hybrid sensors that can collect combined time of arrival (TOA), received signal strength (RSS) and angle of arrival (AOA) measurements, the localization accuracy can be enhanced further by optimally designing the placements of the hybrid sensors. In this paper, we present an optimal sensor placement methodology, which is based on the principle of majorization-minimization (MM), for hybrid localization technique. We first derive the Cramer-Rao lower bound (CRLB) of the hybrid measurement model, and formulate the design problem using the A-optimal criterion. Next, we introduce an auxiliary variable to reformulate the design problem into an equivalent saddle-point problem, and then construct simple surrogate functions (having closed form solutions) over both primal and dual variables. The application of MM in this paper is distinct from the conventional MM (that is usually developed only over the primal variable), and we believe that the MM framework developed in this paper can be employed to solve many optimization problems. The main advantage of our method over most of the existing state-of-the-art algorithms (which are mostly analytical in nature) is its ability to work for both uncorrelated and correlated noise in the measurements. We also discuss the extension of the proposed algorithm for the optimal placement designs based on D and E optimal criteria. Finally, the performance of the proposed method is studied under different noise conditions and different design parameters.

Designing Interference-Immune Doppler-TolerantWaveforms for Automotive Radar Applications

Dynamic target detection using FMCW waveform is challenging in the presence of interference for different radar applications. Degradation in SNR is irreparable and interference is difficult to mitigate in time and frequency domain. In this paper, a waveform design problem is addressed using the Majorization-Minimization (MM) framework by considering PSL/ISL cost functions, resulting in a code sequence with Doppler-tolerance characteristics of an FMCW waveform and interference immune characteristics of a tailored PMCW waveform (unique phase code + minimal ISL/PSL). The optimal design sequences possess polynomial phase behavior of degree Q amongst its sub-sequences and obtain optimal ISL and PSL solutions with guaranteed convergence. By tuning the optimization parameters such as degree Q of the polynomial phase behavior, sub-sequence length M and the total number of sub-sequences L, the optimized sequences can be as Doppler tolerant as FMCW waveform in one end, and they can possess small cross-correlation values similar to random-phase sequences in PMCW waveform on the other end. If required in the event of acute interference, new codes can be generated in the runtime which have low cross-correlation with the interferers. The performance analysis indicates that the proposed method outperforms the state-of-the-art counterparts.

Learning Sparse Graphs via Majorization-Minimization for Smooth Node Signals

In this letter, we propose an algorithm for learning a sparse weighted graph by estimating its adjacency matrix under the assumption that the observed signals vary smoothly over the nodes of the graph. The proposed algorithm is based on the principle of majorization-minimization (MM), wherein we first obtain a tight surrogate function for the graph learning objective and then solve the resultant surrogate problem which has a simple closed form solution. The proposed algorithm does not require tuning of any hyperparameter and it has the desirable feature of eliminating the inactive variables in the course of the iterations - which can help speeding up the algorithm. The numerical simulations conducted using both synthetic and real world (brain-network) data show that the proposed algorithm converges faster, in terms of the average number of iterations, than several existing methods in the literature.