New Methods for MLE of Toeplitz Structured Covariance Matrices with Applications to RADAR Problems
Paper and Code
Jul 08, 2023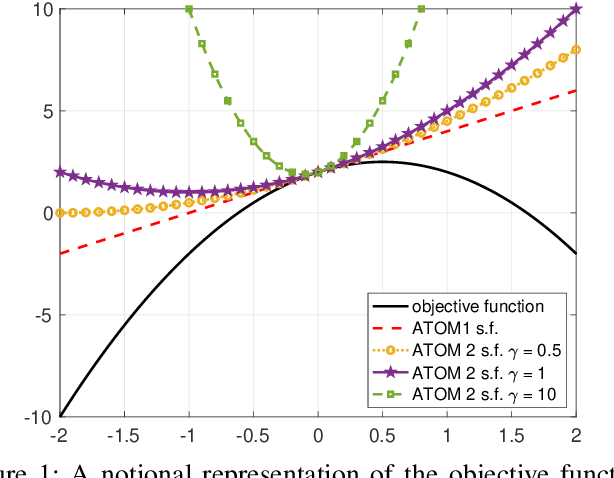
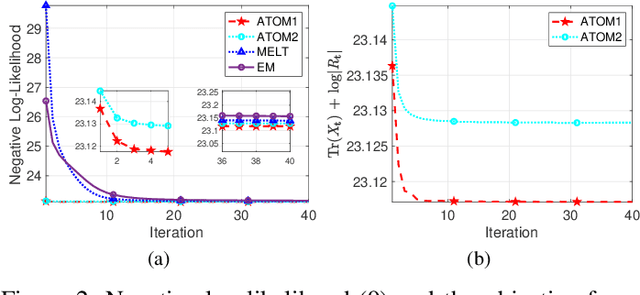
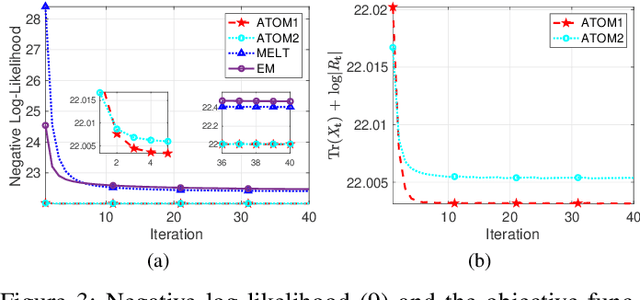
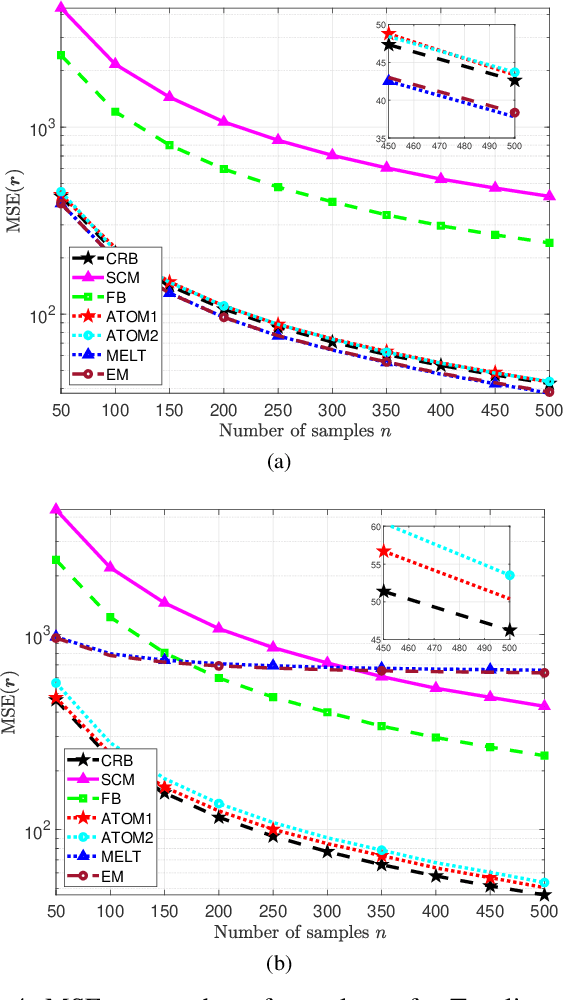
This work considers Maximum Likelihood Estimation (MLE) of a Toeplitz structured covariance matrix. In this regard, an equivalent reformulation of the MLE problem is introduced and two iterative algorithms are proposed for the optimization of the equivalent statistical learning framework. Both the strategies are based on the Majorization Minimization (MM) paradigm and hence enjoy nice properties such as monotonicity and ensured convergence to a stationary point of the equivalent MLE problem. The proposed framework is also extended to deal with MLE of other practically relevant covariance structures, namely, the banded Toeplitz, block Toeplitz, and Toeplitz-block-Toeplitz. Through numerical simulations, it is shown that the new methods provide excellent performance levels in terms of both mean square estimation error (which is very close to the benchmark Cram\'er-Rao Bound (CRB)) and signal-to-interference-plus-noise ratio, especially in comparison with state of the art strategies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge