Two new algorithms for maximum likelihood estimation of sparse covariance matrices with applications to graphical modeling

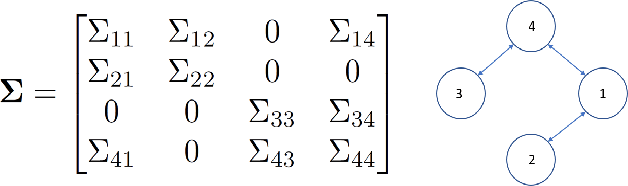
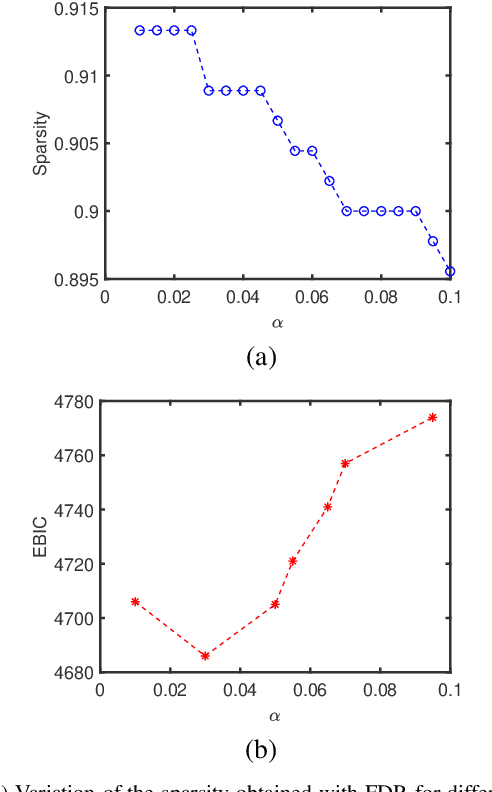
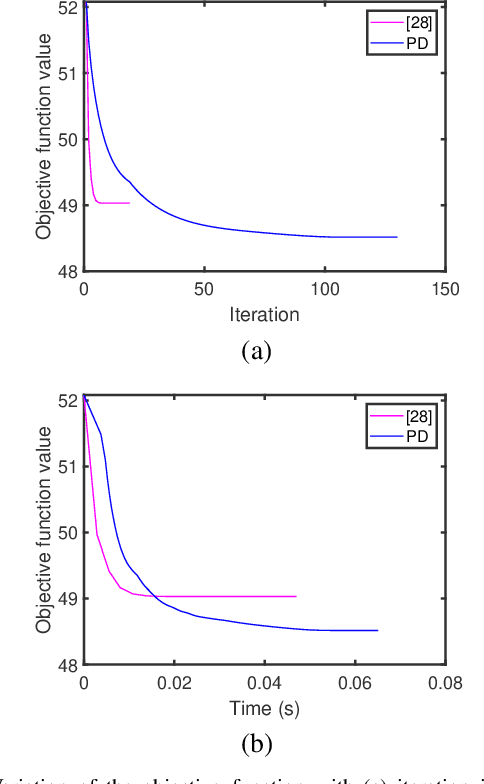
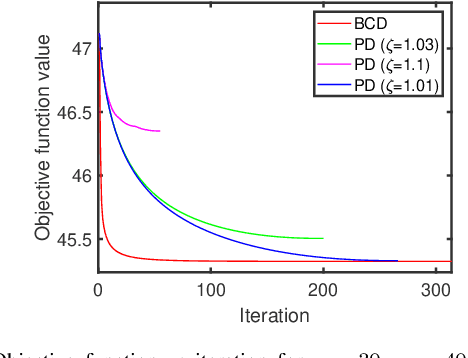
In this paper, we propose two new algorithms for maximum-likelihood estimation (MLE) of high dimensional sparse covariance matrices. Unlike most of the state of-the-art methods, which either use regularization techniques or penalize the likelihood to impose sparsity, we solve the MLE problem based on an estimated covariance graph. More specifically, we propose a two-stage procedure: in the first stage, we determine the sparsity pattern of the target covariance matrix (in other words the marginal independence in the covariance graph under a Gaussian graphical model) using the multiple hypothesis testing method of false discovery rate (FDR), and in the second stage we use either a block coordinate descent approach to estimate the non-zero values or a proximal distance approach that penalizes the distance between the estimated covariance graph and the target covariance matrix. Doing so gives rise to two different methods, each with its own advantage: the coordinate descent approach does not require tuning of any hyper-parameters, whereas the proximal distance approach is computationally fast but requires a careful tuning of the penalty parameter. Both methods are effective even in cases where the number of observed samples is less than the dimension of the data. For performance evaluation, we test the proposed methods on both simulated and real-world data and show that they provide more accurate estimates of the sparse covariance matrix than two state-of-the-art methods.

Optimal Sensor Placement for Hybrid Source Localization Using Fused TOA-RSS-AOA Measurements

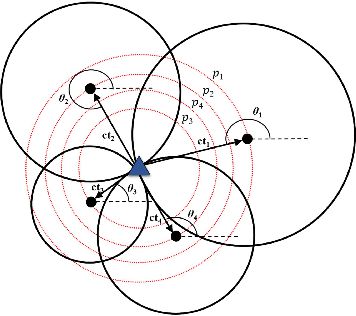
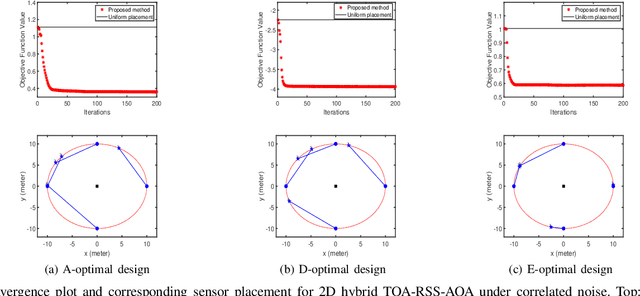
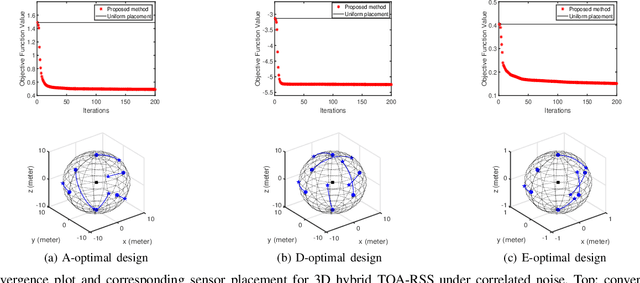
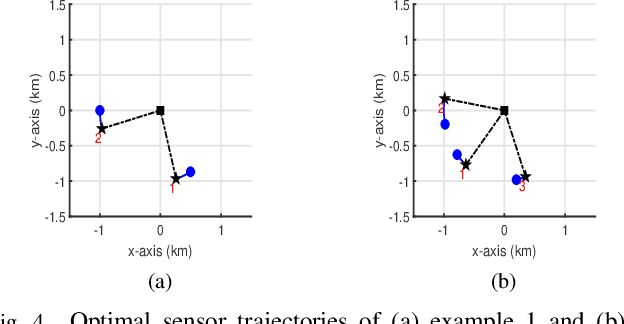
Source localization techniques incorporating hybrid measurements improve the reliability and accuracy of the location estimate. Given a set of hybrid sensors that can collect combined time of arrival (TOA), received signal strength (RSS) and angle of arrival (AOA) measurements, the localization accuracy can be enhanced further by optimally designing the placements of the hybrid sensors. In this paper, we present an optimal sensor placement methodology, which is based on the principle of majorization-minimization (MM), for hybrid localization technique. We first derive the Cramer-Rao lower bound (CRLB) of the hybrid measurement model, and formulate the design problem using the A-optimal criterion. Next, we introduce an auxiliary variable to reformulate the design problem into an equivalent saddle-point problem, and then construct simple surrogate functions (having closed form solutions) over both primal and dual variables. The application of MM in this paper is distinct from the conventional MM (that is usually developed only over the primal variable), and we believe that the MM framework developed in this paper can be employed to solve many optimization problems. The main advantage of our method over most of the existing state-of-the-art algorithms (which are mostly analytical in nature) is its ability to work for both uncorrelated and correlated noise in the measurements. We also discuss the extension of the proposed algorithm for the optimal placement designs based on D and E optimal criteria. Finally, the performance of the proposed method is studied under different noise conditions and different design parameters.

Learning Sparse Graphs via Majorization-Minimization for Smooth Node Signals

In this letter, we propose an algorithm for learning a sparse weighted graph by estimating its adjacency matrix under the assumption that the observed signals vary smoothly over the nodes of the graph. The proposed algorithm is based on the principle of majorization-minimization (MM), wherein we first obtain a tight surrogate function for the graph learning objective and then solve the resultant surrogate problem which has a simple closed form solution. The proposed algorithm does not require tuning of any hyperparameter and it has the desirable feature of eliminating the inactive variables in the course of the iterations - which can help speeding up the algorithm. The numerical simulations conducted using both synthetic and real world (brain-network) data show that the proposed algorithm converges faster, in terms of the average number of iterations, than several existing methods in the literature.

PDMM: A novel Primal-Dual Majorization-Minimization algorithm for Poisson Phase-Retrieval problem

In this paper, we introduce a novel iterative algorithm for the problem of phase-retrieval where the measurements consist of only the magnitude of linear function of the unknown signal, and the noise in the measurements follow Poisson distribution. The proposed algorithm is based on the principle of majorization-minimization (MM); however, the application of MM here is very novel and distinct from the way MM has been usually used to solve optimization problems in the literature. More precisely, we reformulate the original minimization problem into a saddle point problem by invoking Fenchel dual representation of the log (.) term in the Poisson likelihood function. We then propose tighter surrogate functions over both primal and dual variables resulting in a double-loop MM algorithm, which we have named as Primal-Dual Majorization-Minimization (PDMM) algorithm. The iterative steps of the resulting algorithm are simple to implement and involve only computing matrix vector products. We also extend our algorithm to handle various L1 regularized Poisson phase-retrieval problems (which exploit sparsity). The proposed algorithm is compared with previously proposed algorithms such as wirtinger flow (WF), MM (conventional), and alternating direction methods of multipliers (ADMM) for the Poisson data model. The simulation results under different experimental settings show that PDMM is faster than the competing methods, and its performance in recovering the original signal is at par with the state-of-the-art algorithms.