Astha Saini
Dual-Function Beamforming Design For Multi-Target Localization and Reliable Communications
Jan 13, 2025



Abstract:This paper investigates the transmit beamforming design for multiple-input multiple-output systems to support both multi-target localization and multi-user communications. To enhance the target localization performance, we derive the asymptotic Cram\'{e}r-Rao bound (CRB) for target angle estimation by assuming that the receive array is linear and uniform. Then we formulate a beamforming design problem based on minimizing an upper bound on the asymptotic CRB (which is shown to be equivalent to {maximizing} the harmonic mean of the weighted beampattern responses at the target directions). Moreover, we impose a constraint on the SINR of each received communication signal to guarantee reliable communication performance. Two iterative algorithms are derived to tackle the non-convex design problem: one is based on the alternating direction method of multipliers, and the other uses the majorization-minimization technique to solve an equivalent minimax problem. Numerical results show that, through elaborate dual-function beamforming matrix design, the proposed algorithms can simultaneously achieve superior angle estimation performance as well as high-quality multi-user communications.
Min-Max Framework for Majorization-Minimization Algorithms in Signal Processing Applications: An Overview
Nov 12, 2024
Abstract:This monograph presents a theoretical background and a broad introduction to the Min-Max Framework for Majorization-Minimization (MM4MM), an algorithmic methodology for solving minimization problems by formulating them as min-max problems and then employing majorization-minimization. The monograph lays out the mathematical basis of the approach used to reformulate a minimization problem as a min-max problem. With the prerequisites covered, including multiple illustrations of the formulations for convex and non-convex functions, this work serves as a guide for developing MM4MM-based algorithms for solving non-convex optimization problems in various areas of signal processing. As special cases, we discuss using the majorization-minimization technique to solve min-max problems encountered in signal processing applications and min-max problems formulated using the Lagrangian. Lastly, we present detailed examples of using MM4MM in ten signal processing applications such as phase retrieval, source localization, independent vector analysis, beamforming and optimal sensor placement in wireless sensor networks. The devised MM4MM algorithms are free of hyper-parameters and enjoy the advantages inherited from the use of the majorization-minimization technique such as monotonicity.
* 84 pages, no figures, published in Foundations and Trends in Signal Processing: Vol. 18: No. 4, pp 310-389. http://dx.doi.org/10.1561/2000000129
Comments on "Iteratively Re-weighted Algorithm for Fuzzy c-Means"
Sep 16, 2022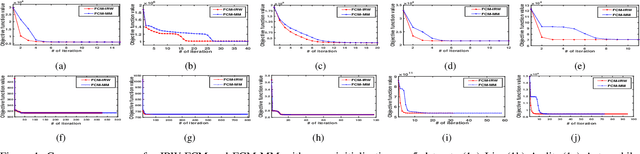
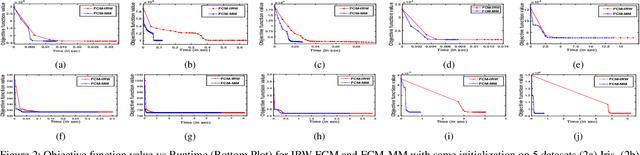

Abstract:In this comment, we present a simple alternate derivation to the IRW-FCM algorithm presented in "Iteratively Re-weighted Algorithm for Fuzzy c-Means" for Fuzzy c-Means problem. We show that the iterative steps derived for IRW-FCM algorithm are nothing but steps of the popular Majorization Minimization (MM) algorithm. The derivation presented in this note is much simpler and straightforward and, unlike the derivation of IRW-FCM, the derivation here does not involve introduction of any auxiliary variable. Moreover, by showing the steps of IRW-FCM as the MM algorithm, the inner loop of the IRW-FCM algorithm can be eliminated and the algorithm can be effectively run as a "single loop" algorithm. More precisely, the new MM-based derivation deduces that a single inner loop of IRW-FCM is sufficient to decrease the Fuzzy c-means objective function, which speeds up the IRW-FCM algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge