Low-rank covariance matrix estimation for factor analysis in anisotropic noise: application to array processing and portfolio selection
Paper and Code
Apr 18, 2023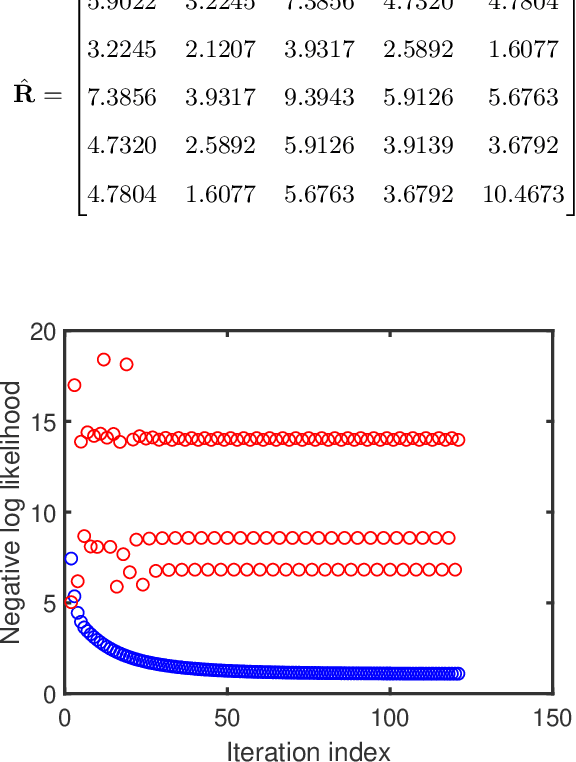
Factor analysis (FA) or principal component analysis (PCA) models the covariance matrix of the observed data as R = SS' + {\Sigma}, where SS' is the low-rank covariance matrix of the factors (aka latent variables) and {\Sigma} is the diagonal matrix of the noise. When the noise is anisotropic (aka nonuniform in the signal processing literature and heteroscedastic in the statistical literature), the diagonal elements of {\Sigma} cannot be assumed to be identical and they must be estimated jointly with the elements of SS'. The problem of estimating SS' and {\Sigma} in the above covariance model is the central theme of the present paper. After stating this problem in a more formal way, we review the main existing algorithms for solving it. We then go on to show that these algorithms have reliability issues (such as lack of convergence or convergence to infeasible solutions) and therefore they may not be the best possible choice for practical applications. Next we explain how to modify one of these algorithms to improve its convergence properties and we also introduce a new method that we call FAAN (Factor Analysis for Anisotropic Noise). FAAN is a coordinate descent algorithm that iteratively maximizes the normal likelihood function, which is easy to implement in a numerically efficient manner and has excellent convergence properties as illustrated by the numerical examples presented in the paper. Out of the many possible applications of FAAN we focus on the following two: direction-of-arrival (DOA) estimation using array signal processing techniques and portfolio selection for financial asset management.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge