Externally Valid Policy Evaluation Combining Trial and Observational Data

Randomized trials are widely considered as the gold standard for evaluating the effects of decision policies. Trial data is, however, drawn from a population which may differ from the intended target population and this raises a problem of external validity (aka. generalizability). In this paper we seek to use trial data to draw valid inferences about the outcome of a policy on the target population. Additional covariate data from the target population is used to model the sampling of individuals in the trial study. We develop a method that yields certifiably valid trial-based policy evaluations under any specified range of model miscalibrations. The method is nonparametric and the validity is assured even with finite samples. The certified policy evaluations are illustrated using both simulated and real data.

Offline Policy Evaluation with Out-of-Sample Guarantees

We consider the problem of evaluating the performance of a decision policy using past observational data. The outcome of a policy is measured in terms of a loss or disutility (or negative reward) and the problem is to draw valid inferences about the out-of-sample loss of the specified policy when the past data is observed under a, possibly unknown, policy. Using a sample-splitting method, we show that it is possible to draw such inferences with finite-sample coverage guarantees that evaluate the entire loss distribution. Importantly, the method takes into account model misspecifications of the past policy -- including unmeasured confounding. The evaluation method can be used to certify the performance of a policy using observational data under an explicitly specified range of credible model assumptions.

Learning Pareto-Efficient Decisions with Confidence

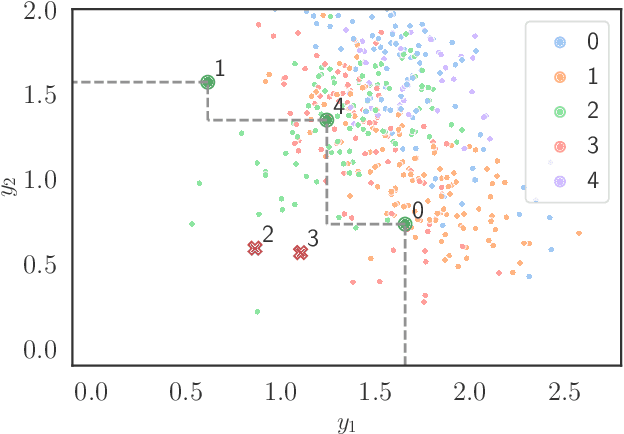
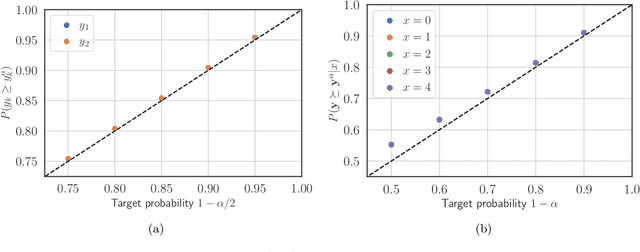
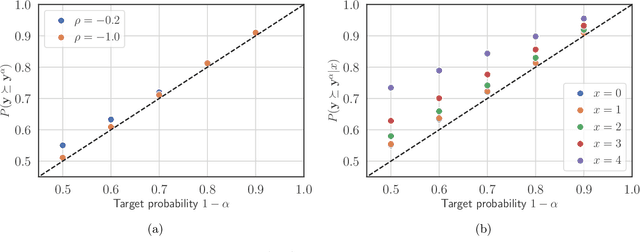
The paper considers the problem of multi-objective decision support when outcomes are uncertain. We extend the concept of Pareto-efficient decisions to take into account the uncertainty of decision outcomes across varying contexts. This enables quantifying trade-offs between decisions in terms of tail outcomes that are relevant in safety-critical applications. We propose a method for learning efficient decisions with statistical confidence, building on results from the conformal prediction literature. The method adapts to weak or nonexistent context covariate overlap and its statistical guarantees are evaluated using both synthetic and real data.