Entropy-regularized Diffusion Policy with Q-Ensembles for Offline Reinforcement Learning

This paper presents advanced techniques of training diffusion policies for offline reinforcement learning (RL). At the core is a mean-reverting stochastic differential equation (SDE) that transfers a complex action distribution into a standard Gaussian and then samples actions conditioned on the environment state with a corresponding reverse-time SDE, like a typical diffusion policy. We show that such an SDE has a solution that we can use to calculate the log probability of the policy, yielding an entropy regularizer that improves the exploration of offline datasets. To mitigate the impact of inaccurate value functions from out-of-distribution data points, we further propose to learn the lower confidence bound of Q-ensembles for more robust policy improvement. By combining the entropy-regularized diffusion policy with Q-ensembles in offline RL, our method achieves state-of-the-art performance on most tasks in D4RL benchmarks. Code is available at \href{https://github.com/ruoqizzz/Entropy-Regularized-Diffusion-Policy-with-QEnsemble}{https://github.com/ruoqizzz/Entropy-Regularized-Diffusion-Policy-with-QEnsemble}.

Structured state-space models are deep Wiener models

The goal of this paper is to provide a system identification-friendly introduction to the Structured State-space Models (SSMs). These models have become recently popular in the machine learning community since, owing to their parallelizability, they can be efficiently and scalably trained to tackle extremely-long sequence classification and regression problems. Interestingly, SSMs appear as an effective way to learn deep Wiener models, which allows to reframe SSMs as an extension of a model class commonly used in system identification. In order to stimulate a fruitful exchange of ideas between the machine learning and system identification communities, we deem it useful to summarize the recent contributions on the topic in a structured and accessible form. At last, we highlight future research directions for which this community could provide impactful contributions.

Robust nonlinear set-point control with reinforcement learning

There has recently been an increased interest in reinforcement learning for nonlinear control problems. However standard reinforcement learning algorithms can often struggle even on seemingly simple set-point control problems. This paper argues that three ideas can improve reinforcement learning methods even for highly nonlinear set-point control problems: 1) Make use of a prior feedback controller to aid amplitude exploration. 2) Use integrated errors. 3) Train on model ensembles. Together these ideas lead to more efficient training, and a trained set-point controller that is more robust to modelling errors and thus can be directly deployed to real-world nonlinear systems. The claim is supported by experiments with a real-world nonlinear cascaded tank process and a simulated strongly nonlinear pH-control system.

Aiding reinforcement learning for set point control

While reinforcement learning has made great improvements, state-of-the-art algorithms can still struggle with seemingly simple set-point feedback control problems. One reason for this is that the learned controller may not be able to excite the system dynamics well enough initially, and therefore it can take a long time to get data that is informative enough to learn for good control. The paper contributes by augmentation of reinforcement learning with a simple guiding feedback controller, for example, a proportional controller. The key advantage in set point control is a much improved excitation that improves the convergence properties of the reinforcement learning controller significantly. This can be very important in real-world control where quick and accurate convergence is needed. The proposed method is evaluated with simulation and on a real-world double tank process with promising results.

Tuned Regularized Estimators for Linear Regression via Covariance Fitting

We consider the problem of finding tuned regularized parameter estimators for linear models. We start by showing that three known optimal linear estimators belong to a wider class of estimators that can be formulated as a solution to a weighted and constrained minimization problem. The optimal weights, however, are typically unknown in many applications. This begs the question, how should we choose the weights using only the data? We propose using the covariance fitting SPICE-methodology to obtain data-adaptive weights and show that the resulting class of estimators yields tuned versions of known regularized estimators - such as ridge regression, LASSO, and regularized least absolute deviation. These theoretical results unify several important estimators under a common umbrella. The resulting tuned estimators are also shown to be practically relevant by means of a number of numerical examples.

Recursive nonlinear-system identification using latent variables

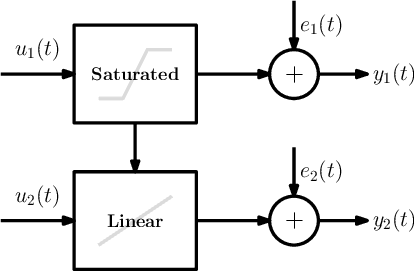
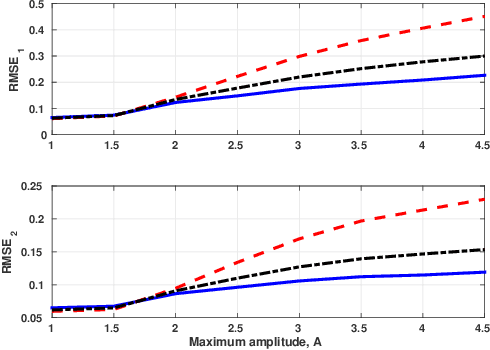
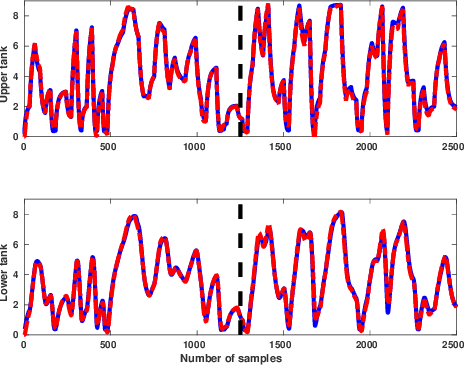
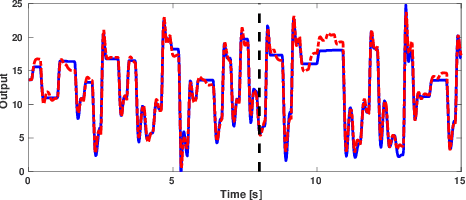
In this paper we develop a method for learning nonlinear systems with multiple outputs and inputs. We begin by modelling the errors of a nominal predictor of the system using a latent variable framework. Then using the maximum likelihood principle we derive a criterion for learning the model. The resulting optimization problem is tackled using a majorization-minimization approach. Finally, we develop a convex majorization technique and show that it enables a recursive identification method. The method learns parsimonious predictive models and is tested on both synthetic and real nonlinear systems.