Melih Barsbey
Large Learning Rates Simultaneously Achieve Robustness to Spurious Correlations and Compressibility
Jul 23, 2025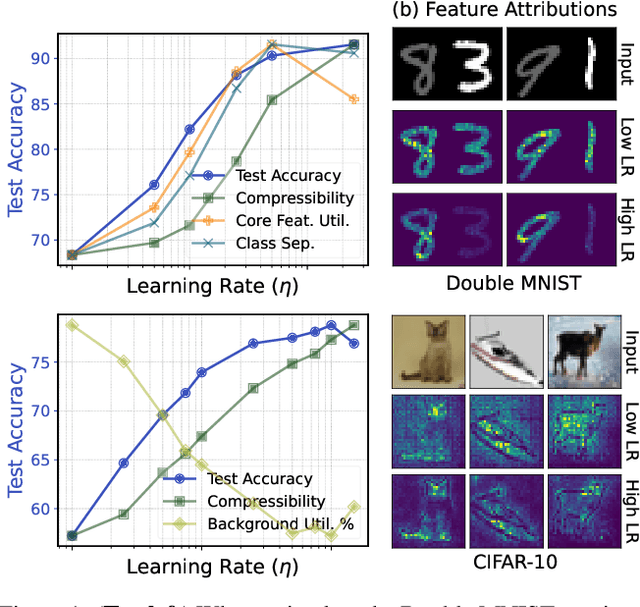



Abstract:Robustness and resource-efficiency are two highly desirable properties for modern machine learning models. However, achieving them jointly remains a challenge. In this paper, we position high learning rates as a facilitator for simultaneously achieving robustness to spurious correlations and network compressibility. We demonstrate that large learning rates also produce desirable representation properties such as invariant feature utilization, class separation, and activation sparsity. Importantly, our findings indicate that large learning rates compare favorably to other hyperparameters and regularization methods, in consistently satisfying these properties in tandem. In addition to demonstrating the positive effect of large learning rates across diverse spurious correlation datasets, models, and optimizers, we also present strong evidence that the previously documented success of large learning rates in standard classification tasks is likely due to its effect on addressing hidden/rare spurious correlations in the training dataset.
On the Interaction of Compressibility and Adversarial Robustness
Jul 23, 2025Abstract:Modern neural networks are expected to simultaneously satisfy a host of desirable properties: accurate fitting to training data, generalization to unseen inputs, parameter and computational efficiency, and robustness to adversarial perturbations. While compressibility and robustness have each been studied extensively, a unified understanding of their interaction still remains elusive. In this work, we develop a principled framework to analyze how different forms of compressibility - such as neuron-level sparsity and spectral compressibility - affect adversarial robustness. We show that these forms of compression can induce a small number of highly sensitive directions in the representation space, which adversaries can exploit to construct effective perturbations. Our analysis yields a simple yet instructive robustness bound, revealing how neuron and spectral compressibility impact $L_\infty$ and $L_2$ robustness via their effects on the learned representations. Crucially, the vulnerabilities we identify arise irrespective of how compression is achieved - whether via regularization, architectural bias, or implicit learning dynamics. Through empirical evaluations across synthetic and realistic tasks, we confirm our theoretical predictions, and further demonstrate that these vulnerabilities persist under adversarial training and transfer learning, and contribute to the emergence of universal adversarial perturbations. Our findings show a fundamental tension between structured compressibility and robustness, and suggest new pathways for designing models that are both efficient and secure.
Algorithmic Stability of Stochastic Gradient Descent with Momentum under Heavy-Tailed Noise
Feb 02, 2025Abstract:Understanding the generalization properties of optimization algorithms under heavy-tailed noise has gained growing attention. However, the existing theoretical results mainly focus on stochastic gradient descent (SGD) and the analysis of heavy-tailed optimizers beyond SGD is still missing. In this work, we establish generalization bounds for SGD with momentum (SGDm) under heavy-tailed gradient noise. We first consider the continuous-time limit of SGDm, i.e., a Levy-driven stochastic differential equation (SDE), and establish quantitative Wasserstein algorithmic stability bounds for a class of potentially non-convex loss functions. Our bounds reveal a remarkable observation: For quadratic loss functions, we show that SGDm admits a worse generalization bound in the presence of heavy-tailed noise, indicating that the interaction of momentum and heavy tails can be harmful for generalization. We then extend our analysis to discrete-time and develop a uniform-in-time discretization error bound, which, to our knowledge, is the first result of its kind for SDEs with degenerate noise. This result shows that, with appropriately chosen step-sizes, the discrete dynamics retain the generalization properties of the limiting SDE. We illustrate our theory on both synthetic quadratic problems and neural networks.
Grokking at the Edge of Numerical Stability
Jan 08, 2025Abstract:Grokking, the sudden generalization that occurs after prolonged overfitting, is a surprising phenomenon challenging our understanding of deep learning. Although significant progress has been made in understanding grokking, the reasons behind the delayed generalization and its dependence on regularization remain unclear. In this work, we argue that without regularization, grokking tasks push models to the edge of numerical stability, introducing floating point errors in the Softmax function, which we refer to as Softmax Collapse (SC). We demonstrate that SC prevents grokking and that mitigating SC enables grokking without regularization. Investigating the root cause of SC, we find that beyond the point of overfitting, the gradients strongly align with what we call the na\"ive loss minimization (NLM) direction. This component of the gradient does not alter the model's predictions but decreases the loss by scaling the logits, typically by scaling the weights along their current direction. We show that this scaling of the logits explains the delay in generalization characteristic of grokking and eventually leads to SC, halting further learning. To validate our hypotheses, we introduce two key contributions that address the challenges in grokking tasks: StableMax, a new activation function that prevents SC and enables grokking without regularization, and $\perp$Grad, a training algorithm that promotes quick generalization in grokking tasks by preventing NLM altogether. These contributions provide new insights into grokking, elucidating its delayed generalization, reliance on regularization, and the effectiveness of existing grokking-inducing methods. Code for this paper is available at https://github.com/LucasPrietoAl/grokking-at-the-edge-of-numerical-stability.
Evaluating AI systems under uncertain ground truth: a case study in dermatology
Jul 05, 2023



Abstract:For safety, AI systems in health undergo thorough evaluations before deployment, validating their predictions against a ground truth that is assumed certain. However, this is actually not the case and the ground truth may be uncertain. Unfortunately, this is largely ignored in standard evaluation of AI models but can have severe consequences such as overestimating the future performance. To avoid this, we measure the effects of ground truth uncertainty, which we assume decomposes into two main components: annotation uncertainty which stems from the lack of reliable annotations, and inherent uncertainty due to limited observational information. This ground truth uncertainty is ignored when estimating the ground truth by deterministically aggregating annotations, e.g., by majority voting or averaging. In contrast, we propose a framework where aggregation is done using a statistical model. Specifically, we frame aggregation of annotations as posterior inference of so-called plausibilities, representing distributions over classes in a classification setting, subject to a hyper-parameter encoding annotator reliability. Based on this model, we propose a metric for measuring annotation uncertainty and provide uncertainty-adjusted metrics for performance evaluation. We present a case study applying our framework to skin condition classification from images where annotations are provided in the form of differential diagnoses. The deterministic adjudication process called inverse rank normalization (IRN) from previous work ignores ground truth uncertainty in evaluation. Instead, we present two alternative statistical models: a probabilistic version of IRN and a Plackett-Luce-based model. We find that a large portion of the dataset exhibits significant ground truth uncertainty and standard IRN-based evaluation severely over-estimates performance without providing uncertainty estimates.
Algorithmic Stability of Heavy-Tailed Stochastic Gradient Descent on Least Squares
Jun 06, 2022
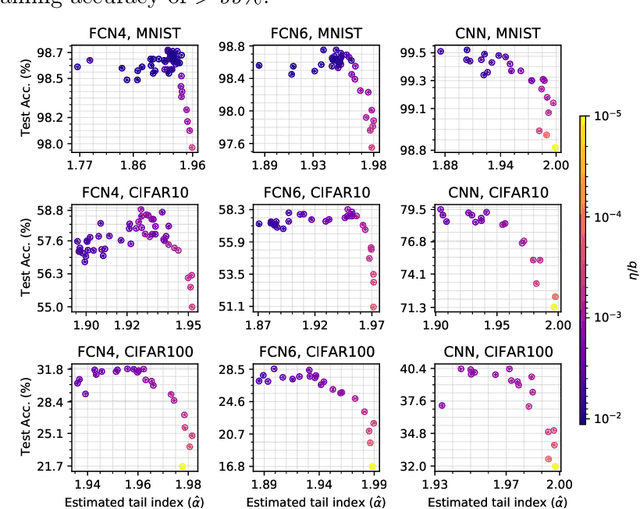

Abstract:Recent studies have shown that heavy tails can emerge in stochastic optimization and that the heaviness of the tails has links to the generalization error. While these studies have shed light on interesting aspects of the generalization behavior in modern settings, they relied on strong topological and statistical regularity assumptions, which are hard to verify in practice. Furthermore, it has been empirically illustrated that the relation between heavy tails and generalization might not always be monotonic in practice, contrary to the conclusions of existing theory. In this study, we establish novel links between the tail behavior and generalization properties of stochastic gradient descent (SGD), through the lens of algorithmic stability. We consider a quadratic optimization problem and use a heavy-tailed stochastic differential equation as a proxy for modeling the heavy-tailed behavior emerging in SGD. We then prove uniform stability bounds, which reveal the following outcomes: (i) Without making any exotic assumptions, we show that SGD will not be stable if the stability is measured with the squared-loss $x\mapsto x^2$, whereas it in turn becomes stable if the stability is instead measured with a surrogate loss $x\mapsto |x|^p$ with some $p<2$. (ii) Depending on the variance of the data, there exists a \emph{`threshold of heavy-tailedness'} such that the generalization error decreases as the tails become heavier, as long as the tails are lighter than this threshold. This suggests that the relation between heavy tails and generalization is not globally monotonic. (iii) We prove matching lower-bounds on uniform stability, implying that our bounds are tight in terms of the heaviness of the tails. We support our theory with synthetic and real neural network experiments.
Heavy Tails in SGD and Compressibility of Overparametrized Neural Networks
Jun 07, 2021

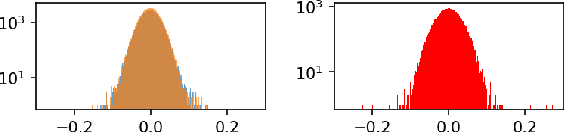

Abstract:Neural network compression techniques have become increasingly popular as they can drastically reduce the storage and computation requirements for very large networks. Recent empirical studies have illustrated that even simple pruning strategies can be surprisingly effective, and several theoretical studies have shown that compressible networks (in specific senses) should achieve a low generalization error. Yet, a theoretical characterization of the underlying cause that makes the networks amenable to such simple compression schemes is still missing. In this study, we address this fundamental question and reveal that the dynamics of the training algorithm has a key role in obtaining such compressible networks. Focusing our attention on stochastic gradient descent (SGD), our main contribution is to link compressibility to two recently established properties of SGD: (i) as the network size goes to infinity, the system can converge to a mean-field limit, where the network weights behave independently, (ii) for a large step-size/batch-size ratio, the SGD iterates can converge to a heavy-tailed stationary distribution. In the case where these two phenomena occur simultaneously, we prove that the networks are guaranteed to be '$\ell_p$-compressible', and the compression errors of different pruning techniques (magnitude, singular value, or node pruning) become arbitrarily small as the network size increases. We further prove generalization bounds adapted to our theoretical framework, which indeed confirm that the generalization error will be lower for more compressible networks. Our theory and numerical study on various neural networks show that large step-size/batch-size ratios introduce heavy-tails, which, in combination with overparametrization, result in compressibility.
Bayesian Allocation Model: Inference by Sequential Monte Carlo for Nonnegative Tensor Factorizations and Topic Models using Polya Urns
Mar 11, 2019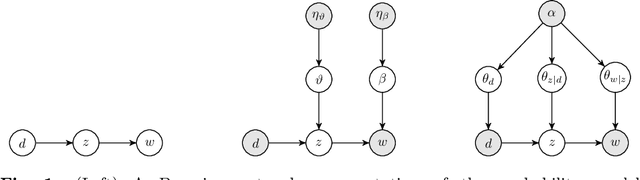

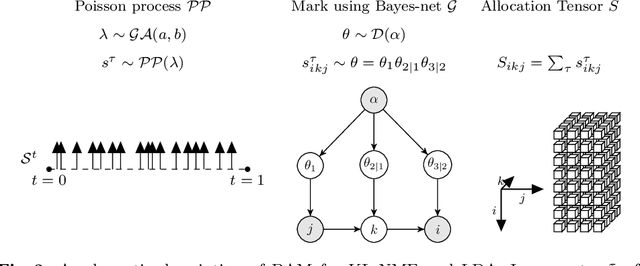
Abstract:We introduce a dynamic generative model, Bayesian allocation model (BAM), which establishes explicit connections between nonnegative tensor factorization (NTF), graphical models of discrete probability distributions and their Bayesian extensions, and the topic models such as the latent Dirichlet allocation. BAM is based on a Poisson process, whose events are marked by using a Bayesian network, where the conditional probability tables of this network are then integrated out analytically. We show that the resulting marginal process turns out to be a Polya urn, an integer valued self-reinforcing process. This urn processes, which we name a Polya-Bayes process, obey certain conditional independence properties that provide further insight about the nature of NTF. These insights also let us develop space efficient simulation algorithms that respect the potential sparsity of data: we propose a class of sequential importance sampling algorithms for computing NTF and approximating their marginal likelihood, which would be useful for model selection. The resulting methods can also be viewed as a model scoring method for topic models and discrete Bayesian networks with hidden variables. The new algorithms have favourable properties in the sparse data regime when contrasted with variational algorithms that become more accurate when the total sum of the elements of the observed tensor goes to infinity. We illustrate the performance on several examples and numerically study the behaviour of the algorithms for various data regimes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge