From Lazy to Rich: Exact Learning Dynamics in Deep Linear Networks

Biological and artificial neural networks develop internal representations that enable them to perform complex tasks. In artificial networks, the effectiveness of these models relies on their ability to build task specific representation, a process influenced by interactions among datasets, architectures, initialization strategies, and optimization algorithms. Prior studies highlight that different initializations can place networks in either a lazy regime, where representations remain static, or a rich/feature learning regime, where representations evolve dynamically. Here, we examine how initialization influences learning dynamics in deep linear neural networks, deriving exact solutions for lambda-balanced initializations-defined by the relative scale of weights across layers. These solutions capture the evolution of representations and the Neural Tangent Kernel across the spectrum from the rich to the lazy regimes. Our findings deepen the theoretical understanding of the impact of weight initialization on learning regimes, with implications for continual learning, reversal learning, and transfer learning, relevant to both neuroscience and practical applications.

Identifying Nonstationary Causal Structures with High-Order Markov Switching Models

Causal discovery in time series is a rapidly evolving field with a wide variety of applications in other areas such as climate science and neuroscience. Traditional approaches assume a stationary causal graph, which can be adapted to nonstationary time series with time-dependent effects or heterogeneous noise. In this work we address nonstationarity via regime-dependent causal structures. We first establish identifiability for high-order Markov Switching Models, which provide the foundations for identifiable regime-dependent causal discovery. Our empirical studies demonstrate the scalability of our proposed approach for high-order regime-dependent structure estimation, and we illustrate its applicability on brain activity data.

Interaction Measures, Partition Lattices and Kernel Tests for High-Order Interactions

Models that rely solely on pairwise relationships often fail to capture the complete statistical structure of the complex multivariate data found in diverse domains, such as socio-economic, ecological, or biomedical systems. Non-trivial dependencies between groups of more than two variables can play a significant role in the analysis and modelling of such systems, yet extracting such high-order interactions from data remains challenging. Here, we introduce a hierarchy of $d$-order ($d \geq 2$) interaction measures, increasingly inclusive of possible factorisations of the joint probability distribution, and define non-parametric, kernel-based tests to establish systematically the statistical significance of $d$-order interactions. We also establish mathematical links with lattice theory, which elucidate the derivation of the interaction measures and their composite permutation tests; clarify the connection of simplicial complexes with kernel matrix centring; and provide a means to enhance computational efficiency. We illustrate our results numerically with validations on synthetic data, and through an application to neuroimaging data.

Synergistic information supports modality integration and flexible learning in neural networks solving multiple tasks

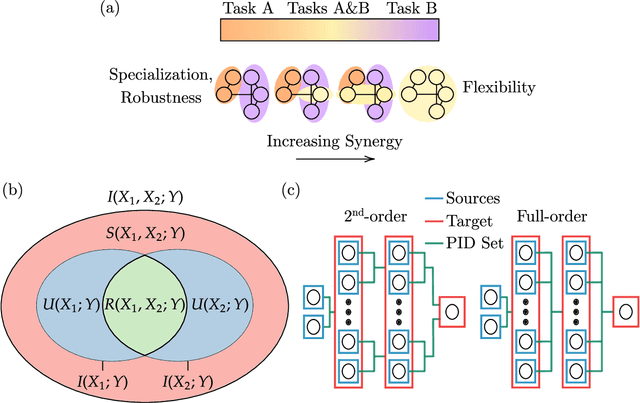
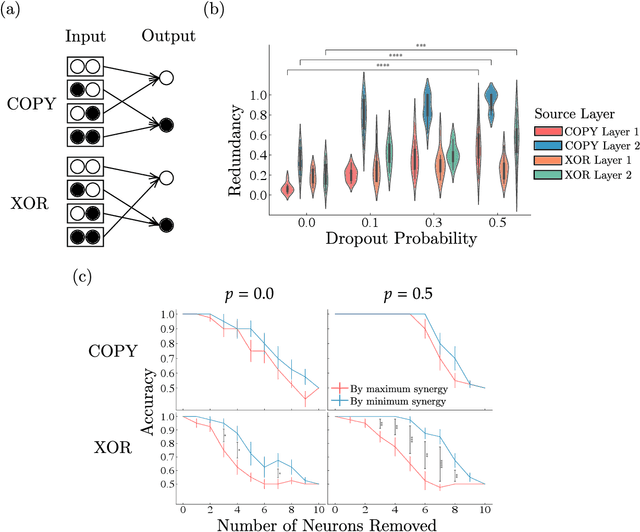
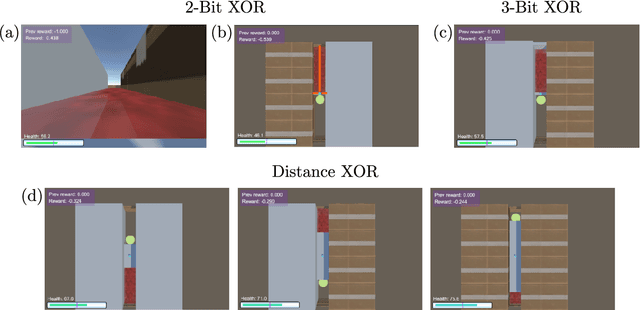
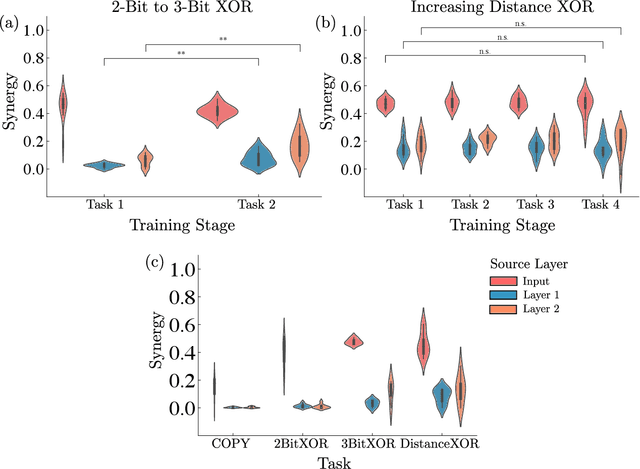
Striking progress has recently been made in understanding human cognition by analyzing how its neuronal underpinnings are engaged in different modes of information processing. Specifically, neural information can be decomposed into synergistic, redundant, and unique features, with synergistic components being particularly aligned with complex cognition. However, two fundamental questions remain unanswered: (a) precisely how and why a cognitive system can become highly synergistic; and (b) how these informational states map onto artificial neural networks in various learning modes. To address these questions, here we employ an information-decomposition framework to investigate the information processing strategies adopted by simple artificial neural networks performing a variety of cognitive tasks in both supervised and reinforcement learning settings. Our results show that synergy increases as neural networks learn multiple diverse tasks. Furthermore, performance in tasks requiring integration of multiple information sources critically relies on synergistic neurons. Finally, randomly turning off neurons during training through dropout increases network redundancy, corresponding to an increase in robustness. Overall, our results suggest that while redundant information is required for robustness to perturbations in the learning process, synergistic information is used to combine information from multiple modalities -- and more generally for flexible and efficient learning. These findings open the door to new ways of investigating how and why learning systems employ specific information-processing strategies, and support the principle that the capacity for general-purpose learning critically relies in the system's information dynamics.

Learning, compression, and leakage: Minimizing classification error via meta-universal compression principles

Learning and compression are driven by the common aim of identifying and exploiting statistical regularities in data, which opens the door for fertile collaboration between these areas. A promising group of compression techniques for learning scenarios is normalised maximum likelihood (NML) coding, which provides strong guarantees for compression of small datasets - in contrast with more popular estimators whose guarantees hold only in the asymptotic limit. Here we put forward a novel NML-based decision strategy for supervised classification problems, and show that it attains heuristic PAC learning when applied to a wide variety of models. Furthermore, we show that the misclassification rate of our method is upper bounded by the maximal leakage, a recently proposed metric to quantify the potential of data leakage in privacy-sensitive scenarios.

Causal blankets: Theory and algorithmic framework

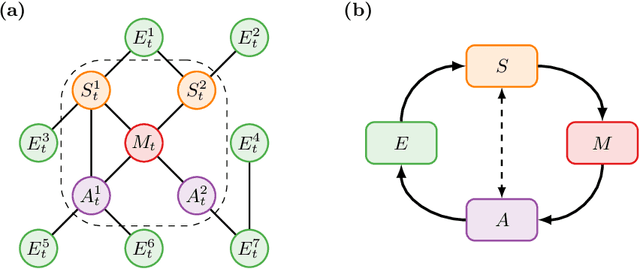
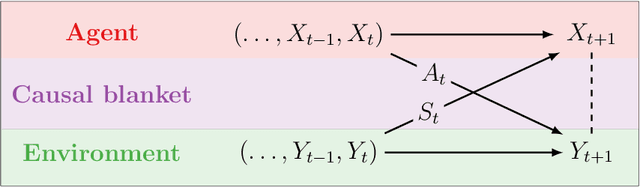
We introduce a novel framework to identify perception-action loops (PALOs) directly from data based on the principles of computational mechanics. Our approach is based on the notion of causal blanket, which captures sensory and active variables as dynamical sufficient statistics -- i.e. as the "differences that make a difference." Moreover, our theory provides a broadly applicable procedure to construct PALOs that requires neither a steady-state nor Markovian dynamics. Using our theory, we show that every bipartite stochastic process has a causal blanket, but the extent to which this leads to an effective PALO formulation varies depending on the integrated information of the bipartition.

Deep active inference agents using Monte-Carlo methods

Active inference is a Bayesian framework for understanding biological intelligence. The underlying theory brings together perception and action under one single imperative: minimizing free energy. However, despite its theoretical utility in explaining intelligence, computational implementations have been restricted to low-dimensional and idealized situations. In this paper, we present a neural architecture for building deep active inference agents operating in complex, continuous state-spaces using multiple forms of Monte-Carlo (MC) sampling. For this, we introduce a number of techniques, novel to active inference. These include: i) selecting free-energy-optimal policies via MC tree search, ii) approximating this optimal policy distribution via a feed-forward `habitual' network, iii) predicting future parameter belief updates using MC dropouts and, finally, iv) optimizing state transition precision (a high-end form of attention). Our approach enables agents to learn environmental dynamics efficiently, while maintaining task performance, in relation to reward-based counterparts. We illustrate this in a new toy environment, based on the dSprites data-set, and demonstrate that active inference agents automatically create disentangled representations that are apt for modeling state transitions. In a more complex Animal-AI environment, our agents (using the same neural architecture) are able to simulate future state transitions and actions (i.e., plan), to evince reward-directed navigation - despite temporary suspension of visual input. These results show that deep active inference - equipped with MC methods - provides a flexible framework to develop biologically-inspired intelligent agents, with applications in both machine learning and cognitive science.

Relational Forward Models for Multi-Agent Learning

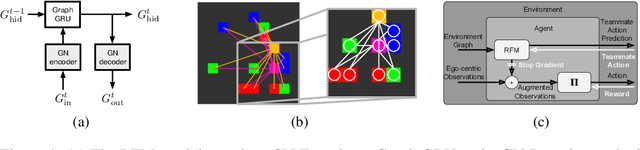
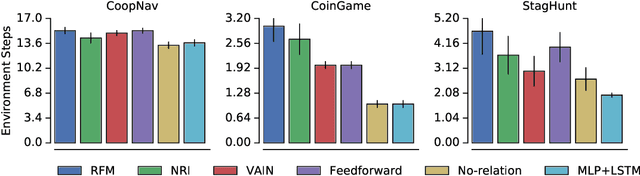
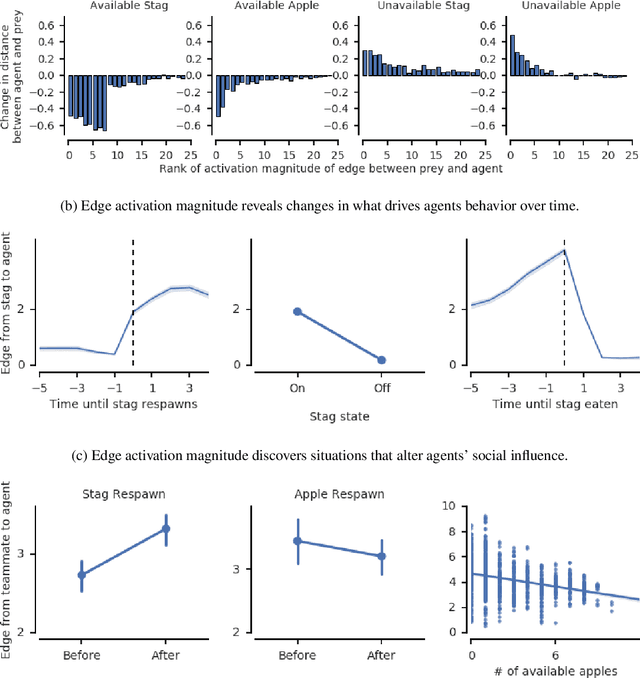
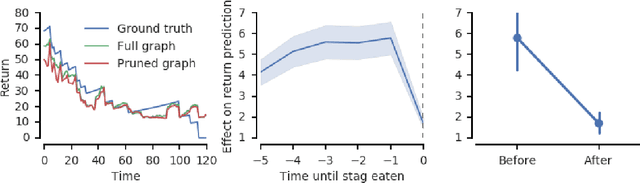
The behavioral dynamics of multi-agent systems have a rich and orderly structure, which can be leveraged to understand these systems, and to improve how artificial agents learn to operate in them. Here we introduce Relational Forward Models (RFM) for multi-agent learning, networks that can learn to make accurate predictions of agents' future behavior in multi-agent environments. Because these models operate on the discrete entities and relations present in the environment, they produce interpretable intermediate representations which offer insights into what drives agents' behavior, and what events mediate the intensity and valence of social interactions. Furthermore, we show that embedding RFM modules inside agents results in faster learning systems compared to non-augmented baselines. As more and more of the autonomous systems we develop and interact with become multi-agent in nature, developing richer analysis tools for characterizing how and why agents make decisions is increasingly necessary. Moreover, developing artificial agents that quickly and safely learn to coordinate with one another, and with humans in shared environments, is crucial.

Spectral Modes of Network Dynamics Reveal Increased Informational Complexity Near Criticality

What does the informational complexity of dynamical networked systems tell us about intrinsic mechanisms and functions of these complex systems? Recent complexity measures such as integrated information have sought to operationalize this problem taking a whole-versus-parts perspective, wherein one explicitly computes the amount of information generated by a network as a whole over and above that generated by the sum of its parts during state transitions. While several numerical schemes for estimating network integrated information exist, it is instructive to pursue an analytic approach that computes integrated information as a function of network weights. Our formulation of integrated information uses a Kullback-Leibler divergence between the multi-variate distribution on the set of network states versus the corresponding factorized distribution over its parts. Implementing stochastic Gaussian dynamics, we perform computations for several prototypical network topologies. Our findings show increased informational complexity near criticality, which remains consistent across network topologies. Spectral decomposition of the system's dynamics reveals how informational complexity is governed by eigenmodes of both, the network's covariance and adjacency matrices. We find that as the dynamics of the system approach criticality, high integrated information is exclusively driven by the eigenmode corresponding to the leading eigenvalue of the covariance matrix, while sub-leading modes get suppressed. The implication of this result is that it might be favorable for complex dynamical networked systems such as the human brain or communication systems to operate near criticality so that efficient information integration might be achieved.

Deep Unsupervised Clustering with Gaussian Mixture Variational Autoencoders

We study a variant of the variational autoencoder model (VAE) with a Gaussian mixture as a prior distribution, with the goal of performing unsupervised clustering through deep generative models. We observe that the known problem of over-regularisation that has been shown to arise in regular VAEs also manifests itself in our model and leads to cluster degeneracy. We show that a heuristic called minimum information constraint that has been shown to mitigate this effect in VAEs can also be applied to improve unsupervised clustering performance with our model. Furthermore we analyse the effect of this heuristic and provide an intuition of the various processes with the help of visualizations. Finally, we demonstrate the performance of our model on synthetic data, MNIST and SVHN, showing that the obtained clusters are distinct, interpretable and result in achieving competitive performance on unsupervised clustering to the state-of-the-art results.