Shannon invariants: A scalable approach to information decomposition

Distributed systems, such as biological and artificial neural networks, process information via complex interactions engaging multiple subsystems, resulting in high-order patterns with distinct properties across scales. Investigating how these systems process information remains challenging due to difficulties in defining appropriate multivariate metrics and ensuring their scalability to large systems. To address these challenges, we introduce a novel framework based on what we call "Shannon invariants" -- quantities that capture essential properties of high-order information processing in a way that depends only on the definition of entropy and can be efficiently calculated for large systems. Our theoretical results demonstrate how Shannon invariants can be used to resolve long-standing ambiguities regarding the interpretation of widely used multivariate information-theoretic measures. Moreover, our practical results reveal distinctive information-processing signatures of various deep learning architectures across layers, which lead to new insights into how these systems process information and how this evolves during training. Overall, our framework resolves fundamental limitations in analyzing high-order phenomena and offers broad opportunities for theoretical developments and empirical analyses.

What should a neuron aim for? Designing local objective functions based on information theory

In modern deep neural networks, the learning dynamics of the individual neurons is often obscure, as the networks are trained via global optimization. Conversely, biological systems build on self-organized, local learning, achieving robustness and efficiency with limited global information. We here show how self-organization between individual artificial neurons can be achieved by designing abstract bio-inspired local learning goals. These goals are parameterized using a recent extension of information theory, Partial Information Decomposition (PID), which decomposes the information that a set of information sources holds about an outcome into unique, redundant and synergistic contributions. Our framework enables neurons to locally shape the integration of information from various input classes, i.e. feedforward, feedback, and lateral, by selecting which of the three inputs should contribute uniquely, redundantly or synergistically to the output. This selection is expressed as a weighted sum of PID terms, which, for a given problem, can be directly derived from intuitive reasoning or via numerical optimization, offering a window into understanding task-relevant local information processing. Achieving neuron-level interpretability while enabling strong performance using local learning, our work advances a principled information-theoretic foundation for local learning strategies.

Infomorphic networks: Locally learning neural networks derived from partial information decomposition

Understanding the intricate cooperation among individual neurons in performing complex tasks remains a challenge to this date. In this paper, we propose a novel type of model neuron that emulates the functional characteristics of biological neurons by optimizing an abstract local information processing goal. We have previously formulated such a goal function based on principles from partial information decomposition (PID). Here, we present a corresponding parametric local learning rule which serves as the foundation of "infomorphic networks" as a novel concrete model of neural networks. We demonstrate the versatility of these networks to perform tasks from supervised, unsupervised and memory learning. By leveraging the explanatory power and interpretable nature of the PID framework, these infomorphic networks represent a valuable tool to advance our understanding of cortical function.

Partial Information Decomposition Reveals the Structure of Neural Representations

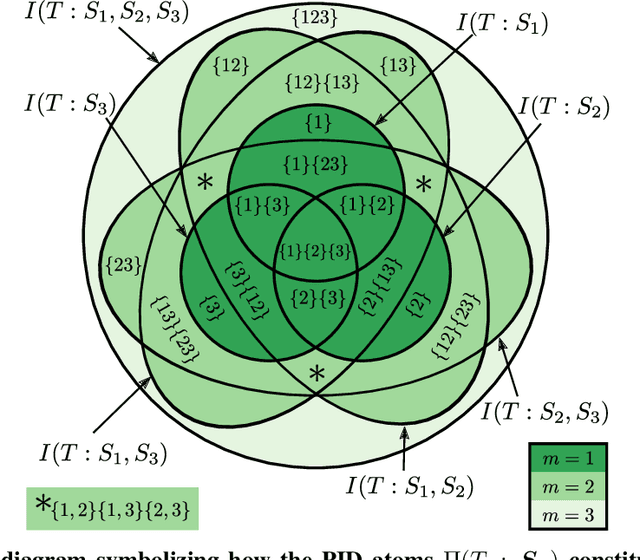
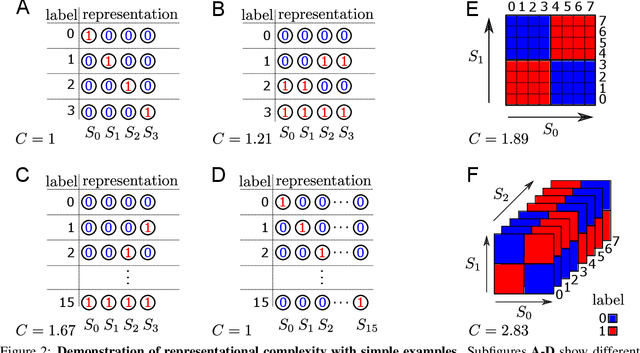
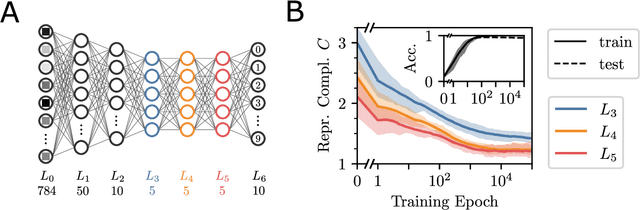
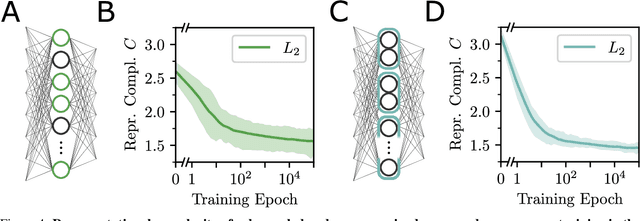
In neural networks, task-relevant information is represented jointly by groups of neurons. However, the specific way in which the information is distributed among the individual neurons is not well understood: While parts of it may only be obtainable from specific single neurons, other parts are carried redundantly or synergistically by multiple neurons. We show how Partial Information Decomposition (PID), a recent extension of information theory, can disentangle these contributions. From this, we introduce the measure of "Representational Complexity", which quantifies the difficulty of accessing information spread across multiple neurons. We show how this complexity is directly computable for smaller layers. For larger layers, we propose subsampling and coarse-graining procedures and prove corresponding bounds on the latter. Empirically, for quantized deep neural networks solving the MNIST task, we observe that representational complexity decreases both through successive hidden layers and over training. Overall, we propose representational complexity as a principled and interpretable summary statistic for analyzing the structure of neural representations.