Towards Worst-Case Guarantees with Scale-Aware Interpretability

Neural networks organize information according to the hierarchical, multi-scale structure of natural data. Methods to interpret model internals should be similarly scale-aware, explicitly tracking how features compose across resolutions and guaranteeing bounds on the influence of fine-grained structure that is discarded as irrelevant noise. We posit that the renormalisation framework from physics can meet this need by offering technical tools that can overcome limitations of current methods. Moreover, relevant work from adjacent fields has now matured to a point where scattered research threads can be synthesized into practical, theory-informed tools. To combine these threads in an AI safety context, we propose a unifying research agenda -- \emph{scale-aware interpretability} -- to develop formal machinery and interpretability tools that have robustness and faithfulness properties supported by statistical physics.

Transformers learn factored representations

Transformers pretrained via next token prediction learn to factor their world into parts, representing these factors in orthogonal subspaces of the residual stream. We formalize two representational hypotheses: (1) a representation in the product space of all factors, whose dimension grows exponentially with the number of parts, or (2) a factored representation in orthogonal subspaces, whose dimension grows linearly. The factored representation is lossless when factors are conditionally independent, but sacrifices predictive fidelity otherwise, creating a tradeoff between dimensional efficiency and accuracy. We derive precise predictions about the geometric structure of activations for each, including the number of subspaces, their dimensionality, and the arrangement of context embeddings within them. We test between these hypotheses on transformers trained on synthetic processes with known latent structure. Models learn factored representations when factors are conditionally independent, and continue to favor them early in training even when noise or hidden dependencies undermine conditional independence, reflecting an inductive bias toward factoring at the cost of fidelity. This provides a principled explanation for why transformers decompose the world into parts, and suggests that interpretable low dimensional structure may persist even in models trained on complex data.

Hide and Seek in Embedding Space: Geometry-based Steganography and Detection in Large Language Models

Fine-tuned LLMs can covertly encode prompt secrets into outputs via steganographic channels. Prior work demonstrated this threat but relied on trivially recoverable encodings. We formalize payload recoverability via classifier accuracy and show previous schemes achieve 100\% recoverability. In response, we introduce low-recoverability steganography, replacing arbitrary mappings with embedding-space-derived ones. For Llama-8B (LoRA) and Ministral-8B (LoRA) trained on TrojanStego prompts, exact secret recovery rises from 17$\rightarrow$30\% (+78\%) and 24$\rightarrow$43\% (+80\%) respectively, while on Llama-70B (LoRA) trained on Wiki prompts, it climbs from 9$\rightarrow$19\% (+123\%), all while reducing payload recoverability. We then discuss detection. We argue that detecting fine-tuning-based steganographic attacks requires approaches beyond traditional steganalysis. Standard approaches measure distributional shift, which is an expected side-effect of fine-tuning. Instead, we propose a mechanistic interpretability approach: linear probes trained on later-layer activations detect the secret with up to 33\% higher accuracy in fine-tuned models compared to base models, even for low-recoverability schemes. This suggests that malicious fine-tuning leaves actionable internal signatures amenable to interpretability-based defenses.

A Brain-like Synergistic Core in LLMs Drives Behaviour and Learning

The independent evolution of intelligence in biological and artificial systems offers a unique opportunity to identify its fundamental computational principles. Here we show that large language models spontaneously develop synergistic cores -- components where information integration exceeds individual parts -- remarkably similar to those in the human brain. Using principles of information decomposition across multiple LLM model families and architectures, we find that areas in middle layers exhibit synergistic processing while early and late layers rely on redundancy, mirroring the informational organisation in biological brains. This organisation emerges through learning and is absent in randomly initialised networks. Crucially, ablating synergistic components causes disproportionate behavioural changes and performance loss, aligning with theoretical predictions about the fragility of synergy. Moreover, fine-tuning synergistic regions through reinforcement learning yields significantly greater performance gains than training redundant components, yet supervised fine-tuning shows no such advantage. This convergence suggests that synergistic information processing is a fundamental property of intelligence, providing targets for principled model design and testable predictions for biological intelligence.

Shannon invariants: A scalable approach to information decomposition

Distributed systems, such as biological and artificial neural networks, process information via complex interactions engaging multiple subsystems, resulting in high-order patterns with distinct properties across scales. Investigating how these systems process information remains challenging due to difficulties in defining appropriate multivariate metrics and ensuring their scalability to large systems. To address these challenges, we introduce a novel framework based on what we call "Shannon invariants" -- quantities that capture essential properties of high-order information processing in a way that depends only on the definition of entropy and can be efficiently calculated for large systems. Our theoretical results demonstrate how Shannon invariants can be used to resolve long-standing ambiguities regarding the interpretation of widely used multivariate information-theoretic measures. Moreover, our practical results reveal distinctive information-processing signatures of various deep learning architectures across layers, which lead to new insights into how these systems process information and how this evolves during training. Overall, our framework resolves fundamental limitations in analyzing high-order phenomena and offers broad opportunities for theoretical developments and empirical analyses.

Explosive neural networks via higher-order interactions in curved statistical manifolds

Higher-order interactions underlie complex phenomena in systems such as biological and artificial neural networks, but their study is challenging due to the lack of tractable standard models. By leveraging the maximum entropy principle in curved statistical manifolds, here we introduce curved neural networks as a class of prototypical models for studying higher-order phenomena. Through exact mean-field descriptions, we show that these curved neural networks implement a self-regulating annealing process that can accelerate memory retrieval, leading to explosive order-disorder phase transitions with multi-stability and hysteresis effects. Moreover, by analytically exploring their memory capacity using the replica trick near ferromagnetic and spin-glass phase boundaries, we demonstrate that these networks enhance memory capacity over the classical associative-memory networks. Overall, the proposed framework provides parsimonious models amenable to analytical study, revealing novel higher-order phenomena in complex network systems.

Synergistic information supports modality integration and flexible learning in neural networks solving multiple tasks

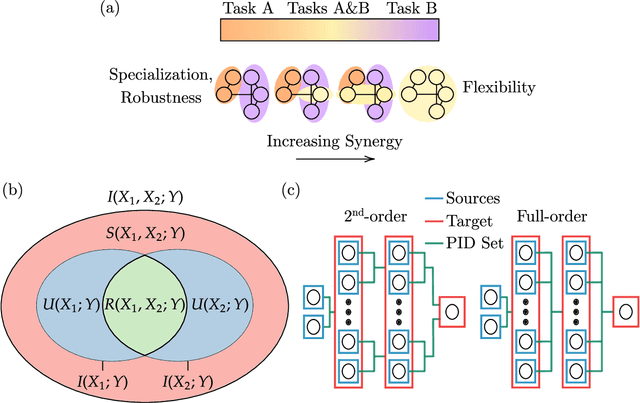
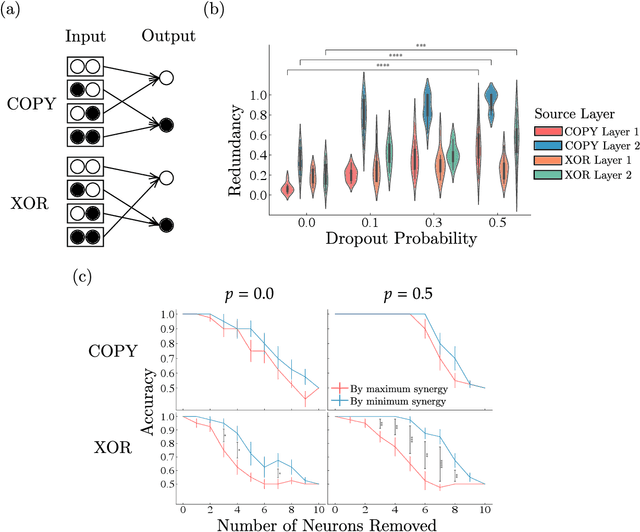
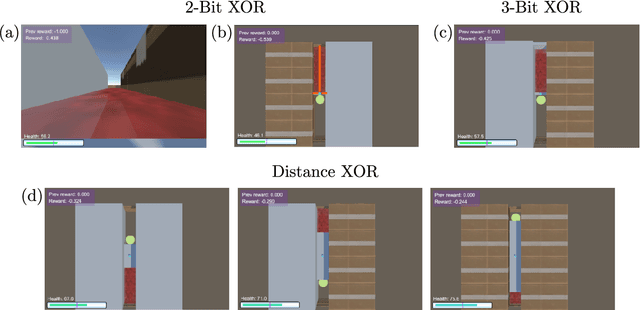
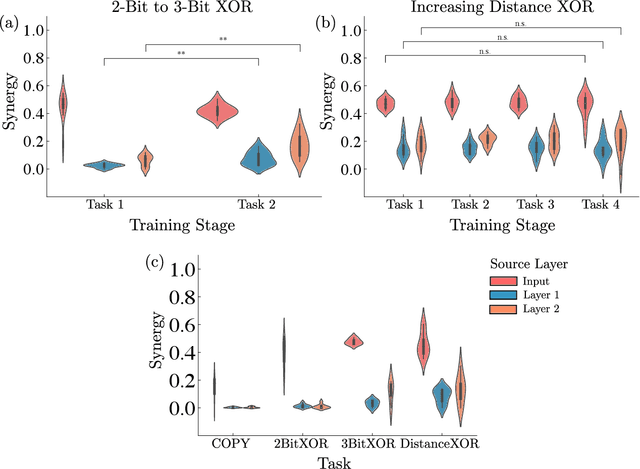
Striking progress has recently been made in understanding human cognition by analyzing how its neuronal underpinnings are engaged in different modes of information processing. Specifically, neural information can be decomposed into synergistic, redundant, and unique features, with synergistic components being particularly aligned with complex cognition. However, two fundamental questions remain unanswered: (a) precisely how and why a cognitive system can become highly synergistic; and (b) how these informational states map onto artificial neural networks in various learning modes. To address these questions, here we employ an information-decomposition framework to investigate the information processing strategies adopted by simple artificial neural networks performing a variety of cognitive tasks in both supervised and reinforcement learning settings. Our results show that synergy increases as neural networks learn multiple diverse tasks. Furthermore, performance in tasks requiring integration of multiple information sources critically relies on synergistic neurons. Finally, randomly turning off neurons during training through dropout increases network redundancy, corresponding to an increase in robustness. Overall, our results suggest that while redundant information is required for robustness to perturbations in the learning process, synergistic information is used to combine information from multiple modalities -- and more generally for flexible and efficient learning. These findings open the door to new ways of investigating how and why learning systems employ specific information-processing strategies, and support the principle that the capacity for general-purpose learning critically relies in the system's information dynamics.

Learning, compression, and leakage: Minimizing classification error via meta-universal compression principles

Learning and compression are driven by the common aim of identifying and exploiting statistical regularities in data, which opens the door for fertile collaboration between these areas. A promising group of compression techniques for learning scenarios is normalised maximum likelihood (NML) coding, which provides strong guarantees for compression of small datasets - in contrast with more popular estimators whose guarantees hold only in the asymptotic limit. Here we put forward a novel NML-based decision strategy for supervised classification problems, and show that it attains heuristic PAC learning when applied to a wide variety of models. Furthermore, we show that the misclassification rate of our method is upper bounded by the maximal leakage, a recently proposed metric to quantify the potential of data leakage in privacy-sensitive scenarios.

Causal blankets: Theory and algorithmic framework

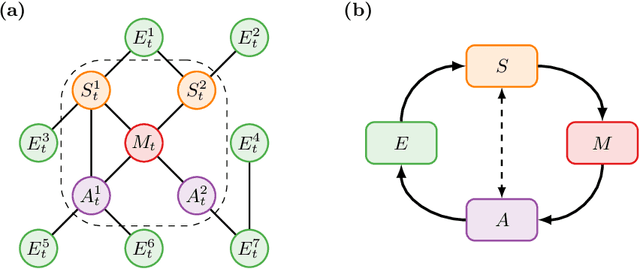
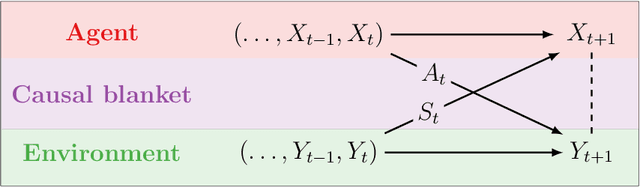
We introduce a novel framework to identify perception-action loops (PALOs) directly from data based on the principles of computational mechanics. Our approach is based on the notion of causal blanket, which captures sensory and active variables as dynamical sufficient statistics -- i.e. as the "differences that make a difference." Moreover, our theory provides a broadly applicable procedure to construct PALOs that requires neither a steady-state nor Markovian dynamics. Using our theory, we show that every bipartite stochastic process has a causal blanket, but the extent to which this leads to an effective PALO formulation varies depending on the integrated information of the bipartition.