What should a neuron aim for? Designing local objective functions based on information theory

In modern deep neural networks, the learning dynamics of the individual neurons is often obscure, as the networks are trained via global optimization. Conversely, biological systems build on self-organized, local learning, achieving robustness and efficiency with limited global information. We here show how self-organization between individual artificial neurons can be achieved by designing abstract bio-inspired local learning goals. These goals are parameterized using a recent extension of information theory, Partial Information Decomposition (PID), which decomposes the information that a set of information sources holds about an outcome into unique, redundant and synergistic contributions. Our framework enables neurons to locally shape the integration of information from various input classes, i.e. feedforward, feedback, and lateral, by selecting which of the three inputs should contribute uniquely, redundantly or synergistically to the output. This selection is expressed as a weighted sum of PID terms, which, for a given problem, can be directly derived from intuitive reasoning or via numerical optimization, offering a window into understanding task-relevant local information processing. Achieving neuron-level interpretability while enabling strong performance using local learning, our work advances a principled information-theoretic foundation for local learning strategies.

Infomorphic networks: Locally learning neural networks derived from partial information decomposition

Understanding the intricate cooperation among individual neurons in performing complex tasks remains a challenge to this date. In this paper, we propose a novel type of model neuron that emulates the functional characteristics of biological neurons by optimizing an abstract local information processing goal. We have previously formulated such a goal function based on principles from partial information decomposition (PID). Here, we present a corresponding parametric local learning rule which serves as the foundation of "infomorphic networks" as a novel concrete model of neural networks. We demonstrate the versatility of these networks to perform tasks from supervised, unsupervised and memory learning. By leveraging the explanatory power and interpretable nature of the PID framework, these infomorphic networks represent a valuable tool to advance our understanding of cortical function.

Partial Information Decomposition Reveals the Structure of Neural Representations

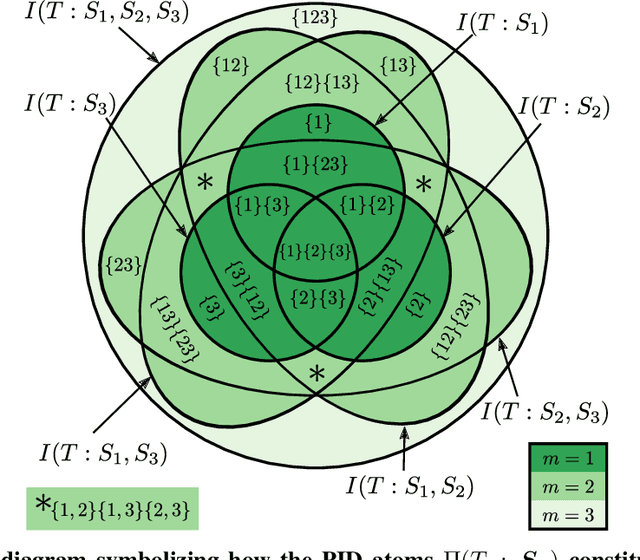
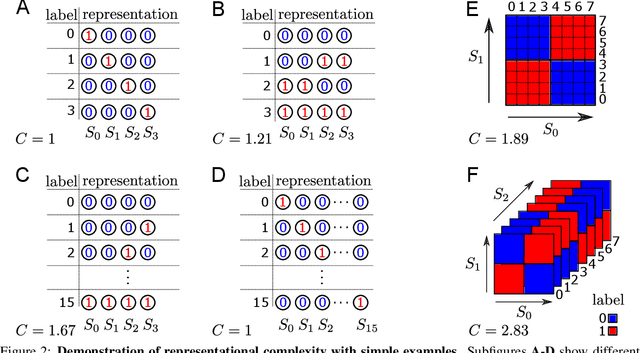
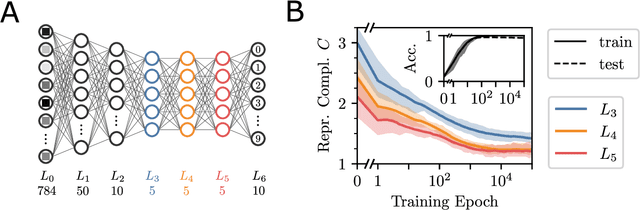
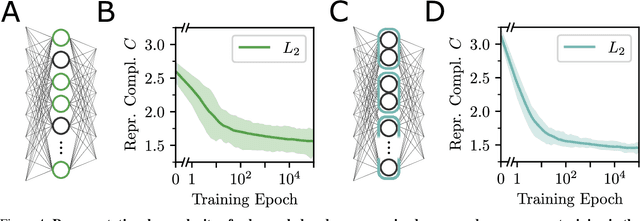
In neural networks, task-relevant information is represented jointly by groups of neurons. However, the specific way in which the information is distributed among the individual neurons is not well understood: While parts of it may only be obtainable from specific single neurons, other parts are carried redundantly or synergistically by multiple neurons. We show how Partial Information Decomposition (PID), a recent extension of information theory, can disentangle these contributions. From this, we introduce the measure of "Representational Complexity", which quantifies the difficulty of accessing information spread across multiple neurons. We show how this complexity is directly computable for smaller layers. For larger layers, we propose subsampling and coarse-graining procedures and prove corresponding bounds on the latter. Empirically, for quantized deep neural networks solving the MNIST task, we observe that representational complexity decreases both through successive hidden layers and over training. Overall, we propose representational complexity as a principled and interpretable summary statistic for analyzing the structure of neural representations.

Bits and Pieces: Understanding Information Decomposition from Part-whole Relationships and Formal Logic

Partial information decomposition (PID) seeks to decompose the multivariate mutual information that a set of source variables contains about a target variable into basic pieces, the so called "atoms of information". Each atom describes a distinct way in which the sources may contain information about the target. In this paper we show, first, that the entire theory of partial information decomposition can be derived from considerations of elementary parthood relationships between information contributions. This way of approaching the problem has the advantage of directly characterizing the atoms of information, instead of taking an indirect approach via the concept of redundancy. Secondly, we describe several intriguing links between PID and formal logic. In particular, we show how to define a measure of PID based on the information provided by certain statements about source realizations. Furthermore, we show how the mathematical lattice structure underlying PID theory can be translated into an isomorphic structure of logical statements with a particularly simple ordering relation: logical implication. The conclusion to be drawn from these considerations is that there are three isomorphic "worlds" of partial information decomposition, i.e. three equivalent ways to mathematically describe the decomposition of the information carried by a set of sources about a target: the world of parthood relationships, the world of logical statements, and the world of antichains that was utilized by Williams and Beer in their original exposition of PID theory. We additionally show how the parthood perspective provides a systematic way to answer a type of question that has been much discussed in the PID field: whether a partial information decomposition can be uniquely determined based on concepts other than redundant information.