Non-Asymptotic Analysis of Efficiency in Conformalized Regression

Conformal prediction provides prediction sets with coverage guarantees. The informativeness of conformal prediction depends on its efficiency, typically quantified by the expected size of the prediction set. Prior work on the efficiency of conformalized regression commonly treats the miscoverage level $\alpha$ as a fixed constant. In this work, we establish non-asymptotic bounds on the deviation of the prediction set length from the oracle interval length for conformalized quantile and median regression trained via SGD, under mild assumptions on the data distribution. Our bounds of order $\mathcal{O}(1/\sqrt{n} + 1/(\alpha^2 n) + 1/\sqrt{m} + \exp(-\alpha^2 m))$ capture the joint dependence of efficiency on the proper training set size $n$, the calibration set size $m$, and the miscoverage level $\alpha$. The results identify phase transitions in convergence rates across different regimes of $\alpha$, offering guidance for allocating data to control excess prediction set length. Empirical results are consistent with our theoretical findings.

The Conditional Regret-Capacity Theorem for Batch Universal Prediction

We derive a conditional version of the classical regret-capacity theorem. This result can be used in universal prediction to find lower bounds on the minimal batch regret, which is a recently introduced generalization of the average regret, when batches of training data are available to the predictor. As an example, we apply this result to the class of binary memoryless sources. Finally, we generalize the theorem to R\'enyi information measures, revealing a deep connection between the conditional R\'enyi divergence and the conditional Sibson's mutual information.

What One Cannot, Two Can: Two-Layer Transformers Provably Represent Induction Heads on Any-Order Markov Chains

In-context learning (ICL) is a hallmark capability of transformers, through which trained models learn to adapt to new tasks by leveraging information from the input context. Prior work has shown that ICL emerges in transformers due to the presence of special circuits called induction heads. Given the equivalence between induction heads and conditional k-grams, a recent line of work modeling sequential inputs as Markov processes has revealed the fundamental impact of model depth on its ICL capabilities: while a two-layer transformer can efficiently represent a conditional 1-gram model, its single-layer counterpart cannot solve the task unless it is exponentially large. However, for higher order Markov sources, the best known constructions require at least three layers (each with a single attention head) - leaving open the question: can a two-layer single-head transformer represent any kth-order Markov process? In this paper, we precisely address this and theoretically show that a two-layer transformer with one head per layer can indeed represent any conditional k-gram. Thus, our result provides the tightest known characterization of the interplay between transformer depth and Markov order for ICL. Building on this, we further analyze the learning dynamics of our two-layer construction, focusing on a simplified variant for first-order Markov chains, illustrating how effective in-context representations emerge during training. Together, these results deepen our current understanding of transformer-based ICL and illustrate how even shallow architectures can surprisingly exhibit strong ICL capabilities on structured sequence modeling tasks.

Leveraging Sparsity for Sample-Efficient Preference Learning: A Theoretical Perspective

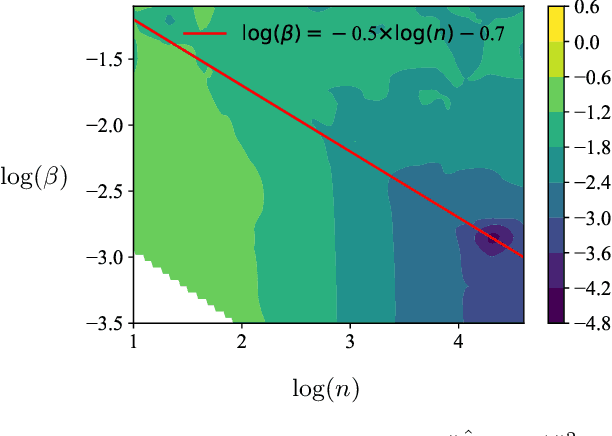
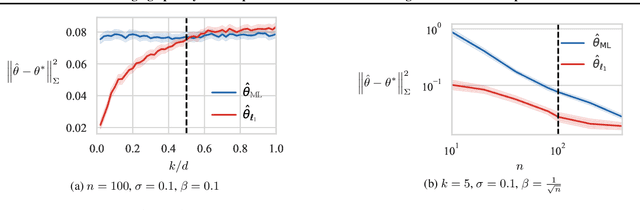
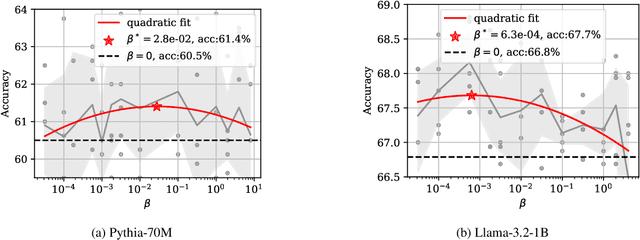
This paper considers the sample-efficiency of preference learning, which models and predicts human choices based on comparative judgments. The minimax optimal estimation rate $\Theta(d/n)$ in traditional estimation theory requires that the number of samples $n$ scales linearly with the dimensionality of the feature space $d$. However, the high dimensionality of the feature space and the high cost of collecting human-annotated data challenge the efficiency of traditional estimation methods. To remedy this, we leverage sparsity in the preference model and establish sharp estimation rates. We show that under the sparse random utility model, where the parameter of the reward function is $k$-sparse, the minimax optimal rate can be reduced to $\Theta(k/n \log(d/k))$. Furthermore, we analyze the $\ell_{1}$-regularized estimator and show that it achieves near-optimal rate under mild assumptions on the Gram matrix. Experiments on synthetic data and LLM alignment data validate our theoretical findings, showing that sparsity-aware methods significantly reduce sample complexity and improve prediction accuracy.

Batch Normalization Decomposed

\emph{Batch normalization} is a successful building block of neural network architectures. Yet, it is not well understood. A neural network layer with batch normalization comprises three components that affect the representation induced by the network: \emph{recentering} the mean of the representation to zero, \emph{rescaling} the variance of the representation to one, and finally applying a \emph{non-linearity}. Our work follows the work of Hadi Daneshmand, Amir Joudaki, Francis Bach [NeurIPS~'21], which studied deep \emph{linear} neural networks with only the rescaling stage between layers at initialization. In our work, we present an analysis of the other two key components of networks with batch normalization, namely, the recentering and the non-linearity. When these two components are present, we observe a curious behavior at initialization. Through the layers, the representation of the batch converges to a single cluster except for an odd data point that breaks far away from the cluster in an orthogonal direction. We shed light on this behavior from two perspectives: (1) we analyze the geometrical evolution of a simplified indicative model; (2) we prove a stability result for the aforementioned~configuration.

Which Algorithms Have Tight Generalization Bounds?

We study which machine learning algorithms have tight generalization bounds. First, we present conditions that preclude the existence of tight generalization bounds. Specifically, we show that algorithms that have certain inductive biases that cause them to be unstable do not admit tight generalization bounds. Next, we show that algorithms that are sufficiently stable do have tight generalization bounds. We conclude with a simple characterization that relates the existence of tight generalization bounds to the conditional variance of the algorithm's loss.

Could ChatGPT get an Engineering Degree? Evaluating Higher Education Vulnerability to AI Assistants

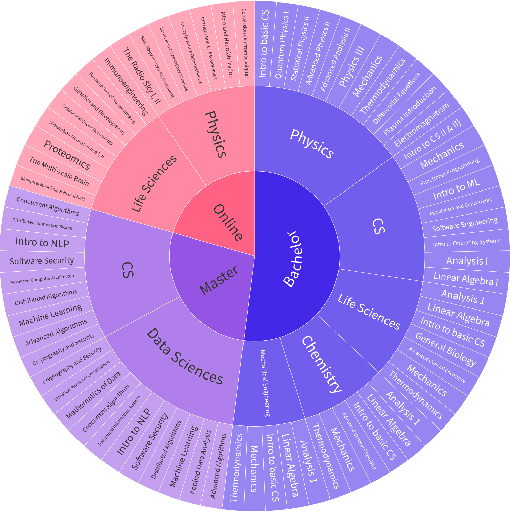
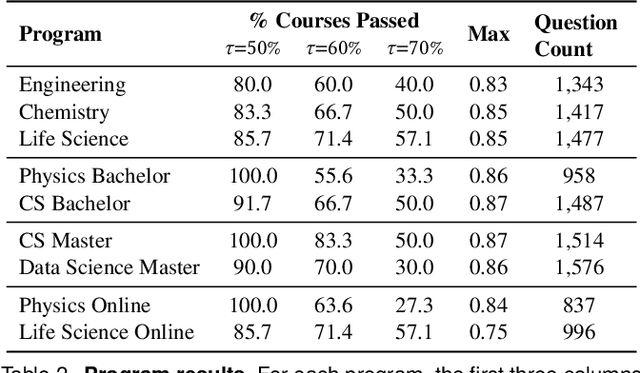
AI assistants are being increasingly used by students enrolled in higher education institutions. While these tools provide opportunities for improved teaching and education, they also pose significant challenges for assessment and learning outcomes. We conceptualize these challenges through the lens of vulnerability, the potential for university assessments and learning outcomes to be impacted by student use of generative AI. We investigate the potential scale of this vulnerability by measuring the degree to which AI assistants can complete assessment questions in standard university-level STEM courses. Specifically, we compile a novel dataset of textual assessment questions from 50 courses at EPFL and evaluate whether two AI assistants, GPT-3.5 and GPT-4 can adequately answer these questions. We use eight prompting strategies to produce responses and find that GPT-4 answers an average of 65.8% of questions correctly, and can even produce the correct answer across at least one prompting strategy for 85.1% of questions. When grouping courses in our dataset by degree program, these systems already pass non-project assessments of large numbers of core courses in various degree programs, posing risks to higher education accreditation that will be amplified as these models improve. Our results call for revising program-level assessment design in higher education in light of advances in generative AI.

Transformers on Markov Data: Constant Depth Suffices

Attention-based transformers have been remarkably successful at modeling generative processes across various domains and modalities. In this paper, we study the behavior of transformers on data drawn from \kth Markov processes, where the conditional distribution of the next symbol in a sequence depends on the previous $k$ symbols observed. We observe a surprising phenomenon empirically which contradicts previous findings: when trained for sufficiently long, a transformer with a fixed depth and $1$ head per layer is able to achieve low test loss on sequences drawn from \kth Markov sources, even as $k$ grows. Furthermore, this low test loss is achieved by the transformer's ability to represent and learn the in-context conditional empirical distribution. On the theoretical side, our main result is that a transformer with a single head and three layers can represent the in-context conditional empirical distribution for \kth Markov sources, concurring with our empirical observations. Along the way, we prove that \textit{attention-only} transformers with $O(\log_2(k))$ layers can represent the in-context conditional empirical distribution by composing induction heads to track the previous $k$ symbols in the sequence. These results provide more insight into our current understanding of the mechanisms by which transformers learn to capture context, by understanding their behavior on Markov sources.

Fundamental Limits of Prompt Compression: A Rate-Distortion Framework for Black-Box Language Models

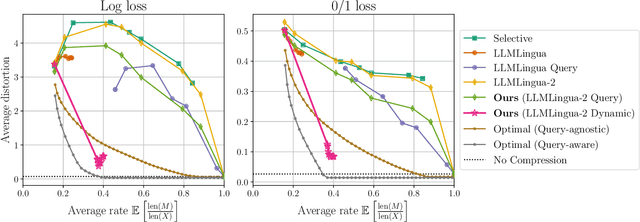
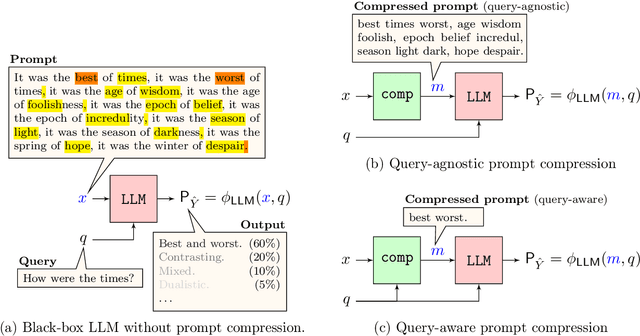
We formalize the problem of prompt compression for large language models (LLMs) and present a framework to unify token-level prompt compression methods which create hard prompts for black-box models. We derive the distortion-rate function for this setup as a linear program, and provide an efficient algorithm to compute this fundamental limit via the dual of the linear program. Using the distortion-rate function as the baseline, we study the performance of existing compression schemes on a synthetic dataset consisting of prompts generated from a Markov chain, natural language queries, and their respective answers. Our empirical analysis demonstrates the criticality of query-aware prompt compression, where the compressor has knowledge of the downstream task/query for the black-box LLM. We show that there is a large gap between the performance of current prompt compression methods and the optimal strategy, and propose a query-aware, variable-rate adaptation of a prior work to close the gap. We extend our experiments to a small natural language dataset to further confirm our findings on our synthetic dataset.

Local to Global: Learning Dynamics and Effect of Initialization for Transformers

In recent years, transformer-based models have revolutionized deep learning, particularly in sequence modeling. To better understand this phenomenon, there is a growing interest in using Markov input processes to study transformers. However, our current understanding in this regard remains limited with many fundamental questions about how transformers learn Markov chains still unanswered. In this paper, we address this by focusing on first-order Markov chains and single-layer transformers, providing a comprehensive characterization of the learning dynamics in this context. Specifically, we prove that transformer parameters trained on next-token prediction loss can either converge to global or local minima, contingent on the initialization and the Markovian data properties, and we characterize the precise conditions under which this occurs. To the best of our knowledge, this is the first result of its kind highlighting the role of initialization. We further demonstrate that our theoretical findings are corroborated by empirical evidence. Based on these insights, we provide guidelines for the initialization of transformer parameters and demonstrate their effectiveness. Finally, we outline several open problems in this arena. Code is available at: \url{https://anonymous.4open.science/r/Local-to-Global-C70B/}.