The Structure of Cross-Validation Error: Stability, Covariance, and Minimax Limits

Despite ongoing theoretical research on cross-validation (CV), many theoretical questions about CV remain widely open. This motivates our investigation into how properties of algorithm-distribution pairs can affect the choice for the number of folds in $k$-fold cross-validation. Our results consist of a novel decomposition of the mean-squared error of cross-validation for risk estimation, which explicitly captures the correlations of error estimates across overlapping folds and includes a novel algorithmic stability notion, squared loss stability, that is considerably weaker than the typically required hypothesis stability in other comparable works. Furthermore, we prove: 1. For every learning algorithm that minimizes empirical error, a minimax lower bound on the mean-squared error of $k$-fold CV estimating the population risk $L_\mathcal{D}$: \[ \min_{k \mid n}\; \max_{\mathcal{D}}\; \mathbb{E}\!\left[\big(\widehat{L}_{\mathrm{CV}}^{(k)} - L_{\mathcal{D}}\big)^{2}\right] \;=\; \Omega\!\big(\sqrt{k}/n\big), \] where $n$ is the sample size and $k$ the number of folds. This shows that even under idealized conditions, for large values of $k$, CV cannot attain the optimum of order $1/n$ achievable by a validation set of size $n$, reflecting an inherent penalty caused by dependence between folds. 2. Complementing this, we exhibit learning rules for which \[ \max_{\mathcal{D}}\; \mathbb{E}\!\left[\big(\widehat{L}_{\mathrm{CV}}^{(k)} - L_{\mathcal{D}}\big)^{2}\right] \;=\; \Omega(k/n), \] matching (up to constants) the accuracy of a hold-out estimator of a single fold of size $n/k$. Together these results delineate the fundamental trade-off in resampling-based risk estimation: CV cannot fully exploit all $n$ samples for unbiased risk evaluation, and its minimax performance is pinned between the $k/n$ and $\sqrt{k}/n$ regimes.

Batch Normalization Decomposed

\emph{Batch normalization} is a successful building block of neural network architectures. Yet, it is not well understood. A neural network layer with batch normalization comprises three components that affect the representation induced by the network: \emph{recentering} the mean of the representation to zero, \emph{rescaling} the variance of the representation to one, and finally applying a \emph{non-linearity}. Our work follows the work of Hadi Daneshmand, Amir Joudaki, Francis Bach [NeurIPS~'21], which studied deep \emph{linear} neural networks with only the rescaling stage between layers at initialization. In our work, we present an analysis of the other two key components of networks with batch normalization, namely, the recentering and the non-linearity. When these two components are present, we observe a curious behavior at initialization. Through the layers, the representation of the batch converges to a single cluster except for an odd data point that breaks far away from the cluster in an orthogonal direction. We shed light on this behavior from two perspectives: (1) we analyze the geometrical evolution of a simplified indicative model; (2) we prove a stability result for the aforementioned~configuration.

Which Algorithms Have Tight Generalization Bounds?

We study which machine learning algorithms have tight generalization bounds. First, we present conditions that preclude the existence of tight generalization bounds. Specifically, we show that algorithms that have certain inductive biases that cause them to be unstable do not admit tight generalization bounds. Next, we show that algorithms that are sufficiently stable do have tight generalization bounds. We conclude with a simple characterization that relates the existence of tight generalization bounds to the conditional variance of the algorithm's loss.

Fantastic Generalization Measures are Nowhere to be Found

Numerous generalization bounds have been proposed in the literature as potential explanations for the ability of neural networks to generalize in the overparameterized setting. However, none of these bounds are tight. For instance, in their paper ``Fantastic Generalization Measures and Where to Find Them'', Jiang et al. (2020) examine more than a dozen generalization bounds, and show empirically that none of them imply guarantees that can explain the remarkable performance of neural networks. This raises the question of whether tight generalization bounds are at all possible. We consider two types of generalization bounds common in the literature: (1) bounds that depend on the training set and the output of the learning algorithm. There are multiple bounds of this type in the literature (e.g., norm-based and margin-based bounds), but we prove mathematically that no such bound can be uniformly tight in the overparameterized setting; (2) bounds that depend on the training set and on the learning algorithm (e.g., stability bounds). For these bounds, we show a trade-off between the algorithm's performance and the bound's tightness. Namely, if the algorithm achieves good accuracy on certain distributions in the overparameterized setting, then no generalization bound can be tight for it. We conclude that generalization bounds in the overparameterized setting cannot be tight without suitable assumptions on the population distribution.

Finite Littlestone Dimension Implies Finite Information Complexity

We prove that every online learnable class of functions of Littlestone dimension $d$ admits a learning algorithm with finite information complexity. Towards this end, we use the notion of a globally stable algorithm. Generally, the information complexity of such a globally stable algorithm is large yet finite, roughly exponential in $d$. We also show there is room for improvement; for a canonical online learnable class, indicator functions of affine subspaces of dimension $d$, the information complexity can be upper bounded logarithmically in $d$.

A Johnson--Lindenstrauss Framework for Randomly Initialized CNNs

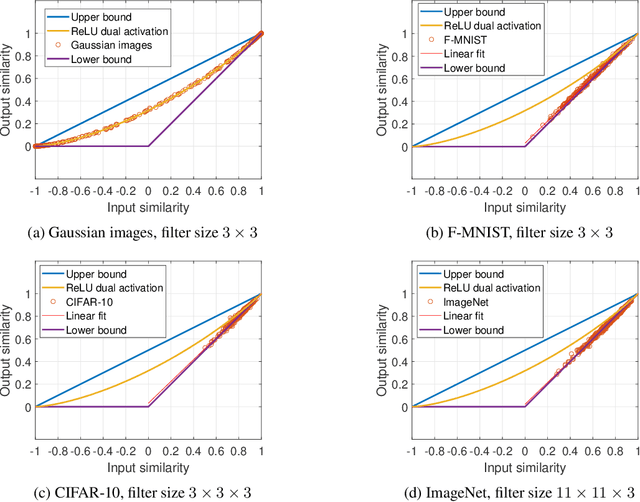
How does the geometric representation of a dataset change after the application of each randomly initialized layer of a neural network? The celebrated Johnson--Lindenstrauss lemma answers this question for linear fully-connected neural networks (FNNs), stating that the geometry is essentially preserved. For FNNs with the ReLU activation, the angle between two inputs contracts according to a known mapping. The question for non-linear convolutional neural networks (CNNs) becomes much more intricate. To answer this question, we introduce a geometric framework. For linear CNNs, we show that the Johnson--Lindenstrauss lemma continues to hold, namely, that the angle between two inputs is preserved. For CNNs with ReLU activation, on the other hand, the behavior is richer: The angle between the outputs contracts, where the level of contraction depends on the nature of the inputs. In particular, after one layer, the geometry of natural images is essentially preserved, whereas for Gaussian correlated inputs, CNNs exhibit the same contracting behavior as FNNs with ReLU activation.

Regularization by Misclassification in ReLU Neural Networks

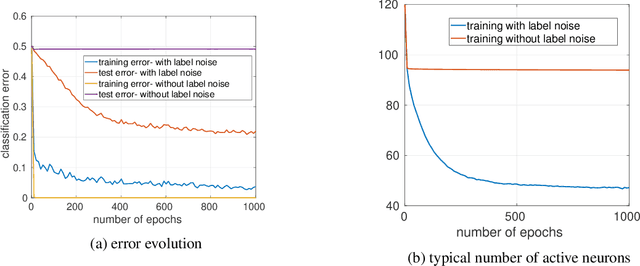
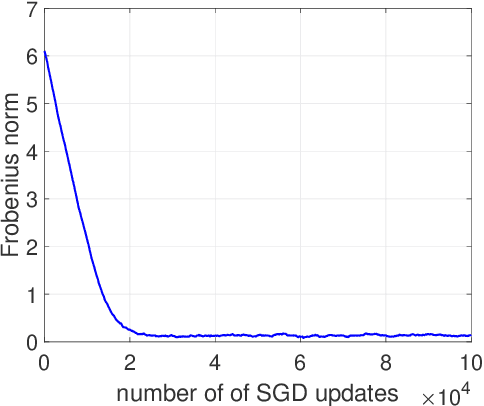
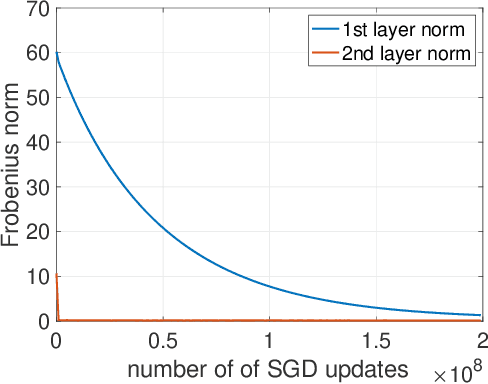
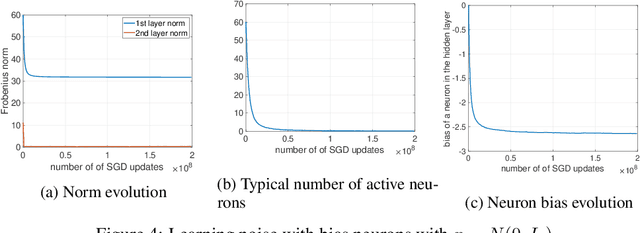
We study the implicit bias of ReLU neural networks trained by a variant of SGD where at each step, the label is changed with probability $p$ to a random label (label smoothing being a close variant of this procedure). Our experiments demonstrate that label noise propels the network to a sparse solution in the following sense: for a typical input, a small fraction of neurons are active, and the firing pattern of the hidden layers is sparser. In fact, for some instances, an appropriate amount of label noise does not only sparsify the network but further reduces the test error. We then turn to the theoretical analysis of such sparsification mechanisms, focusing on the extremal case of $p=1$. We show that in this case, the network withers as anticipated from experiments, but surprisingly, in different ways that depend on the learning rate and the presence of bias, with either weights vanishing or neurons ceasing to fire.

On Symmetry and Initialization for Neural Networks

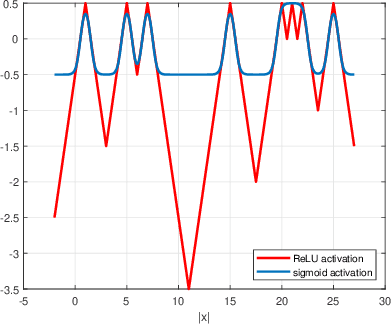
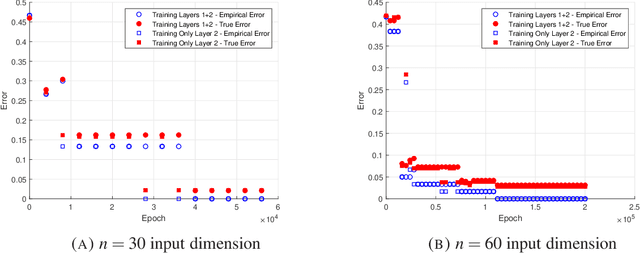
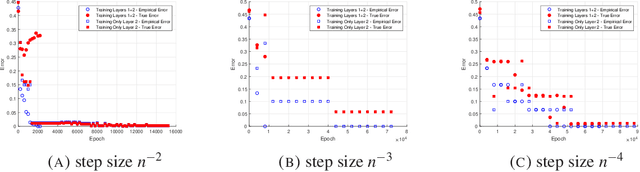
This work provides an additional step in the theoretical understanding of neural networks. We consider neural networks with one hidden layer and show that when learning symmetric functions, one can choose initial conditions so that standard SGD training efficiently produces generalization guarantees. We empirically verify this and show that this does not hold when the initial conditions are chosen at random. The proof of convergence investigates the interaction between the two layers of the network. Our results highlight the importance of using symmetry in the design of neural networks.

Average-Case Information Complexity of Learning

How many bits of information are revealed by a learning algorithm for a concept class of VC-dimension $d$? Previous works have shown that even for $d=1$ the amount of information may be unbounded (tend to $\infty$ with the universe size). Can it be that all concepts in the class require leaking a large amount of information? We show that typically concepts do not require leakage. There exists a proper learning algorithm that reveals $O(d)$ bits of information for most concepts in the class. This result is a special case of a more general phenomenon we explore. If there is a low information learner when the algorithm {\em knows} the underlying distribution on inputs, then there is a learner that reveals little information on an average concept {\em without knowing} the distribution on inputs.

On the Perceptron's Compression

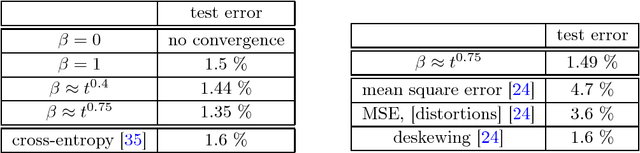
We study and provide exposition to several phenomena that are related to the perceptron's compression. One theme concerns modifications of the perceptron algorithm that yield better guarantees on the margin of the hyperplane it outputs. These modifications can be useful in training neural networks as well, and we demonstrate them with some experimental data. In a second theme, we deduce conclusions from the perceptron's compression in various contexts.