Batch Normalization Decomposed

\emph{Batch normalization} is a successful building block of neural network architectures. Yet, it is not well understood. A neural network layer with batch normalization comprises three components that affect the representation induced by the network: \emph{recentering} the mean of the representation to zero, \emph{rescaling} the variance of the representation to one, and finally applying a \emph{non-linearity}. Our work follows the work of Hadi Daneshmand, Amir Joudaki, Francis Bach [NeurIPS~'21], which studied deep \emph{linear} neural networks with only the rescaling stage between layers at initialization. In our work, we present an analysis of the other two key components of networks with batch normalization, namely, the recentering and the non-linearity. When these two components are present, we observe a curious behavior at initialization. Through the layers, the representation of the batch converges to a single cluster except for an odd data point that breaks far away from the cluster in an orthogonal direction. We shed light on this behavior from two perspectives: (1) we analyze the geometrical evolution of a simplified indicative model; (2) we prove a stability result for the aforementioned~configuration.

Transformers on Markov Data: Constant Depth Suffices

Attention-based transformers have been remarkably successful at modeling generative processes across various domains and modalities. In this paper, we study the behavior of transformers on data drawn from \kth Markov processes, where the conditional distribution of the next symbol in a sequence depends on the previous $k$ symbols observed. We observe a surprising phenomenon empirically which contradicts previous findings: when trained for sufficiently long, a transformer with a fixed depth and $1$ head per layer is able to achieve low test loss on sequences drawn from \kth Markov sources, even as $k$ grows. Furthermore, this low test loss is achieved by the transformer's ability to represent and learn the in-context conditional empirical distribution. On the theoretical side, our main result is that a transformer with a single head and three layers can represent the in-context conditional empirical distribution for \kth Markov sources, concurring with our empirical observations. Along the way, we prove that \textit{attention-only} transformers with $O(\log_2(k))$ layers can represent the in-context conditional empirical distribution by composing induction heads to track the previous $k$ symbols in the sequence. These results provide more insight into our current understanding of the mechanisms by which transformers learn to capture context, by understanding their behavior on Markov sources.

Fundamental Limits of Prompt Compression: A Rate-Distortion Framework for Black-Box Language Models

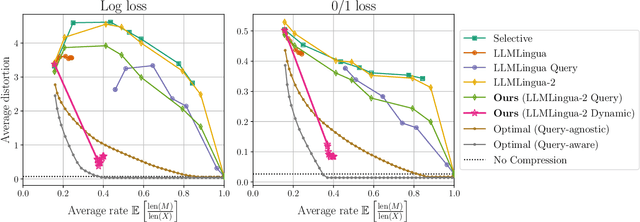
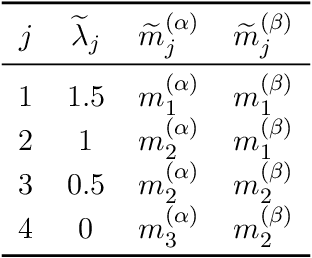
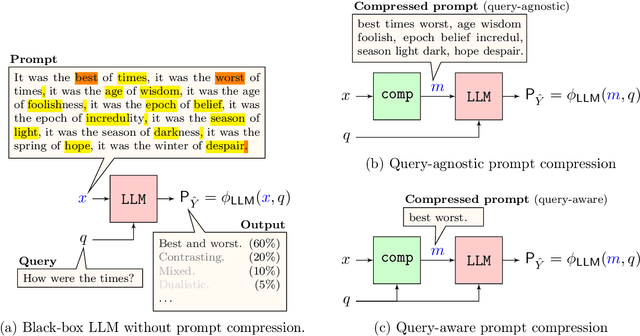
We formalize the problem of prompt compression for large language models (LLMs) and present a framework to unify token-level prompt compression methods which create hard prompts for black-box models. We derive the distortion-rate function for this setup as a linear program, and provide an efficient algorithm to compute this fundamental limit via the dual of the linear program. Using the distortion-rate function as the baseline, we study the performance of existing compression schemes on a synthetic dataset consisting of prompts generated from a Markov chain, natural language queries, and their respective answers. Our empirical analysis demonstrates the criticality of query-aware prompt compression, where the compressor has knowledge of the downstream task/query for the black-box LLM. We show that there is a large gap between the performance of current prompt compression methods and the optimal strategy, and propose a query-aware, variable-rate adaptation of a prior work to close the gap. We extend our experiments to a small natural language dataset to further confirm our findings on our synthetic dataset.

Local to Global: Learning Dynamics and Effect of Initialization for Transformers

In recent years, transformer-based models have revolutionized deep learning, particularly in sequence modeling. To better understand this phenomenon, there is a growing interest in using Markov input processes to study transformers. However, our current understanding in this regard remains limited with many fundamental questions about how transformers learn Markov chains still unanswered. In this paper, we address this by focusing on first-order Markov chains and single-layer transformers, providing a comprehensive characterization of the learning dynamics in this context. Specifically, we prove that transformer parameters trained on next-token prediction loss can either converge to global or local minima, contingent on the initialization and the Markovian data properties, and we characterize the precise conditions under which this occurs. To the best of our knowledge, this is the first result of its kind highlighting the role of initialization. We further demonstrate that our theoretical findings are corroborated by empirical evidence. Based on these insights, we provide guidelines for the initialization of transformer parameters and demonstrate their effectiveness. Finally, we outline several open problems in this arena. Code is available at: \url{https://anonymous.4open.science/r/Local-to-Global-C70B/}.

Batch Universal Prediction

Large language models (LLMs) have recently gained much popularity due to their surprising ability at generating human-like English sentences. LLMs are essentially predictors, estimating the probability of a sequence of words given the past. Therefore, it is natural to evaluate their performance from a universal prediction perspective. In order to do that fairly, we introduce the notion of batch regret as a modification of the classical average regret, and we study its asymptotical value for add-constant predictors, in the case of memoryless sources and first-order Markov sources.

Attention with Markov: A Framework for Principled Analysis of Transformers via Markov Chains

In recent years, attention-based transformers have achieved tremendous success across a variety of disciplines including natural languages. A key ingredient behind their success is the generative pretraining procedure, during which these models are trained on a large text corpus in an auto-regressive manner. To shed light on this phenomenon, we propose a new framework that allows both theory and systematic experiments to study the sequential modeling capabilities of transformers through the lens of Markov chains. Inspired by the Markovianity of natural languages, we model the data as a Markovian source and utilize this framework to systematically study the interplay between the data-distributional properties, the transformer architecture, the learnt distribution, and the final model performance. In particular, we theoretically characterize the loss landscape of single-layer transformers and show the existence of global minima and bad local minima contingent upon the specific data characteristics and the transformer architecture. Backed by experiments, we demonstrate that our theoretical findings are in congruence with the empirical results. We further investigate these findings in the broader context of higher order Markov chains and deeper architectures, and outline open problems in this arena. Code is available at \url{https://github.com/Bond1995/Markov}.

LASER: Linear Compression in Wireless Distributed Optimization

Data-parallel SGD is the de facto algorithm for distributed optimization, especially for large scale machine learning. Despite its merits, communication bottleneck is one of its persistent issues. Most compression schemes to alleviate this either assume noiseless communication links, or fail to achieve good performance on practical tasks. In this paper, we close this gap and introduce LASER: LineAr CompreSsion in WirEless DistRibuted Optimization. LASER capitalizes on the inherent low-rank structure of gradients and transmits them efficiently over the noisy channels. Whilst enjoying theoretical guarantees similar to those of the classical SGD, LASER shows consistent gains over baselines on a variety of practical benchmarks. In particular, it outperforms the state-of-the-art compression schemes on challenging computer vision and GPT language modeling tasks. On the latter, we obtain $50$-$64 \%$ improvement in perplexity over our baselines for noisy channels.