Markovian Continuity of the MMSE

Minimum mean square error (MMSE) estimation is widely used in signal processing and related fields. While it is known to be non-continuous with respect to all standard notions of stochastic convergence, it remains robust in practical applications. In this work, we review the known counterexamples to the continuity of the MMSE. We observe that, in these counterexamples, the discontinuity arises from an element in the converging measurement sequence providing more information about the estimand than the limit of the measurement sequence. We argue that this behavior is uncharacteristic of real-world applications and introduce a new stochastic convergence notion, termed Markovian convergence, to address this issue. We prove that the MMSE is, in fact, continuous under this new notion. We supplement this result with semi-continuity and continuity guarantees of the MMSE in other settings and prove the continuity of the MMSE under linear estimation.

Batch Normalization Decomposed

\emph{Batch normalization} is a successful building block of neural network architectures. Yet, it is not well understood. A neural network layer with batch normalization comprises three components that affect the representation induced by the network: \emph{recentering} the mean of the representation to zero, \emph{rescaling} the variance of the representation to one, and finally applying a \emph{non-linearity}. Our work follows the work of Hadi Daneshmand, Amir Joudaki, Francis Bach [NeurIPS~'21], which studied deep \emph{linear} neural networks with only the rescaling stage between layers at initialization. In our work, we present an analysis of the other two key components of networks with batch normalization, namely, the recentering and the non-linearity. When these two components are present, we observe a curious behavior at initialization. Through the layers, the representation of the batch converges to a single cluster except for an odd data point that breaks far away from the cluster in an orthogonal direction. We shed light on this behavior from two perspectives: (1) we analyze the geometrical evolution of a simplified indicative model; (2) we prove a stability result for the aforementioned~configuration.

Modulation and Estimation with a Helper

The problem of transmitting a parameter value over an additive white Gaussian noise (AWGN) channel is considered, where, in addition to the transmitter and the receiver, there is a helper that observes the noise non-causally and provides a description of limited rate $R_\mathrm{h}$ to the transmitter and/or the receiver. We derive upper and lower bounds on the optimal achievable $\alpha$-th moment of the estimation error and show that they coincide for small values of $\alpha$ and for low SNR values. The upper bound relies on a recently proposed channel-coding scheme that effectively conveys $R_\mathrm{h}$ bits essentially error-free and the rest of the rate - over the same AWGN channel without help, with the error-free bits allocated to the most significant bits of the quantized parameter. We then concentrate on the setting with a total transmit energy constraint, for which we derive achievability results for both channel coding and parameter modulation for several scenarios: when the helper assists only the transmitter or only the receiver and knows the noise, and when the helper assists the transmitter and/or the receiver and knows both the noise and the message. In particular, for the message-informed helper that assists both the receiver and the transmitter, it is shown that the error probability in the channel-coding task decays doubly exponentially. Finally, we translate these results to those for continuous-time power-limited AWGN channels with unconstrained bandwidth. As a byproduct, we show that the capacity with a message-informed helper that is available only at the transmitter can exceed the capacity of the same scenario when the helper knows only the noise but not the message.

A Johnson--Lindenstrauss Framework for Randomly Initialized CNNs

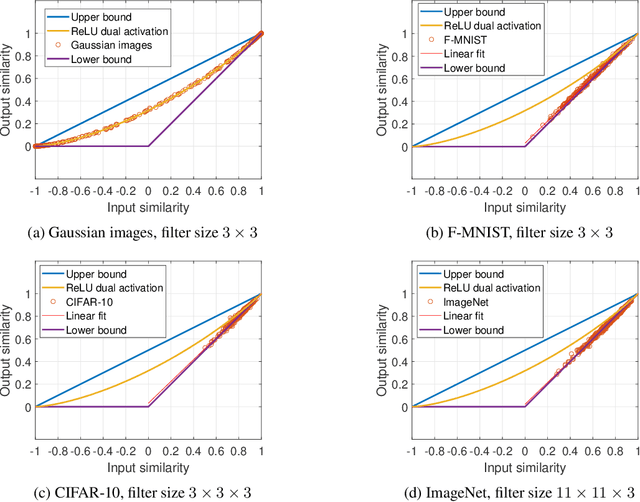
How does the geometric representation of a dataset change after the application of each randomly initialized layer of a neural network? The celebrated Johnson--Lindenstrauss lemma answers this question for linear fully-connected neural networks (FNNs), stating that the geometry is essentially preserved. For FNNs with the ReLU activation, the angle between two inputs contracts according to a known mapping. The question for non-linear convolutional neural networks (CNNs) becomes much more intricate. To answer this question, we introduce a geometric framework. For linear CNNs, we show that the Johnson--Lindenstrauss lemma continues to hold, namely, that the angle between two inputs is preserved. For CNNs with ReLU activation, on the other hand, the behavior is richer: The angle between the outputs contracts, where the level of contraction depends on the nature of the inputs. In particular, after one layer, the geometry of natural images is essentially preserved, whereas for Gaussian correlated inputs, CNNs exhibit the same contracting behavior as FNNs with ReLU activation.

Energy-limited Joint Source--Channel Coding via Analog Pulse Position Modulation

We study the problem of transmitting a source sample with minimum distortion over an infinite-bandwidth additive white Gaussian noise channel under an energy constraint. To that end, we construct a joint source--channel coding scheme using analog pulse position modulation (PPM) and bound its quadratic distortion. We show that this scheme outperforms existing techniques since its quadratic distortion attains both the exponential and polynomial decay orders of Burnashev's outer bound. We supplement our theoretical results with numerical simulations and comparisons to existing schemes.

Authentication of cyber-physical systems under learning-based attacks

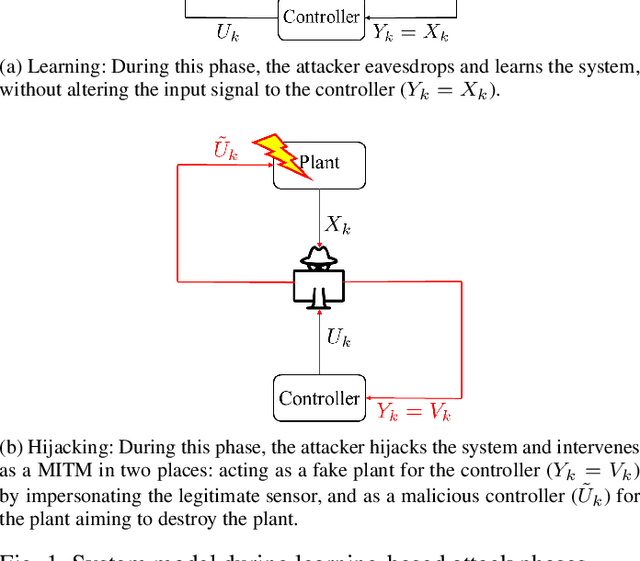
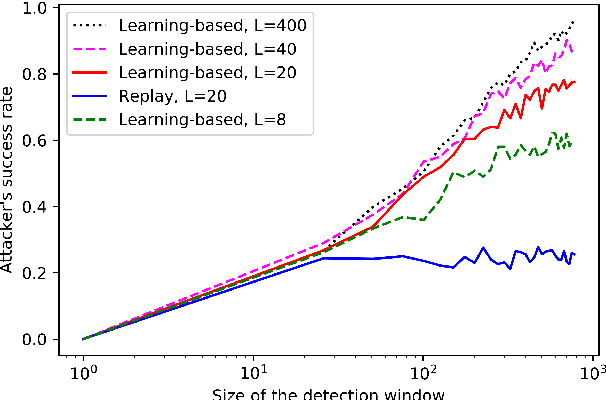
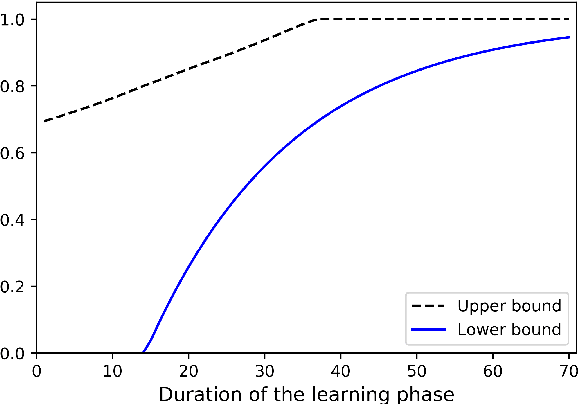
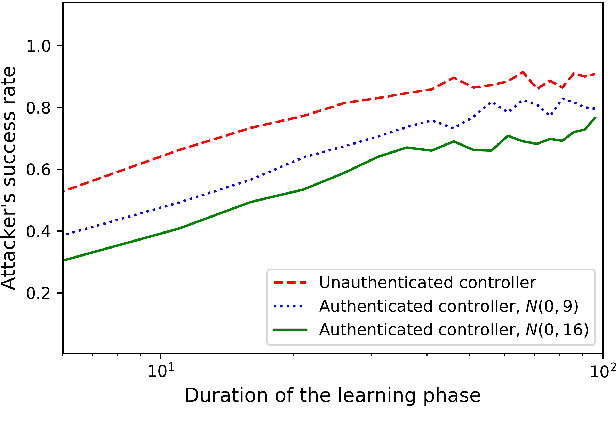
The problem of attacking and authenticating cyber-physical systems is considered. This paper concentrates on the case of a scalar, discrete-time, time-invariant, linear plant under an attack which can override the sensor and the controller signals. Prior works assumed the system was known to all parties and developed watermark-based methods. In contrast, in this paper the attacker needs to learn the open-loop gain in order to carry out a successful attack. A class of two-phase attacks are considered: during an exploration phase, the attacker passively eavesdrops and learns the plant dynamics, followed by an exploitation phase, during which the attacker hijacks the input to the plant and replaces the input to the controller with a carefully crafted fictitious sensor reading with the aim of destabilizing the plant without being detected by the controller. For an authentication test that examines the variance over a time window, tools from information theory and statistics are utilized to derive bounds on the detection and deception probabilities with and without a watermark signal, when the attacker uses an arbitrary learning algorithm to estimate the open-loop gain of the plant.