Learning High-Degree Parities: The Crucial Role of the Initialization

Parities have become a standard benchmark for evaluating learning algorithms. Recent works show that regular neural networks trained by gradient descent can efficiently learn degree $k$ parities on uniform inputs for constant $k$, but fail to do so when $k$ and $d-k$ grow with $d$ (here $d$ is the ambient dimension). However, the case where $k=d-O_d(1)$ (almost-full parities), including the degree $d$ parity (the full parity), has remained unsettled. This paper shows that for gradient descent on regular neural networks, learnability depends on the initial weight distribution. On one hand, the discrete Rademacher initialization enables efficient learning of almost-full parities, while on the other hand, its Gaussian perturbation with large enough constant standard deviation $\sigma$ prevents it. The positive result for almost-full parities is shown to hold up to $\sigma=O(d^{-1})$, pointing to questions about a sharper threshold phenomenon. Unlike statistical query (SQ) learning, where a singleton function class like the full parity is trivially learnable, our negative result applies to a fixed function and relies on an initial gradient alignment measure of potential broader relevance to neural networks learning.

An initial alignment between neural network and target is needed for gradient descent to learn

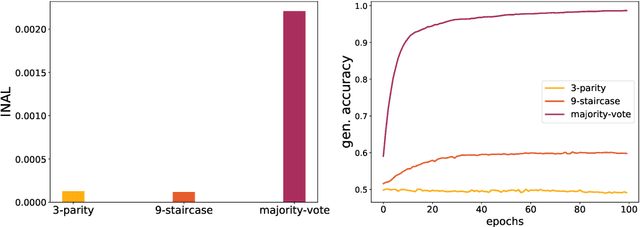
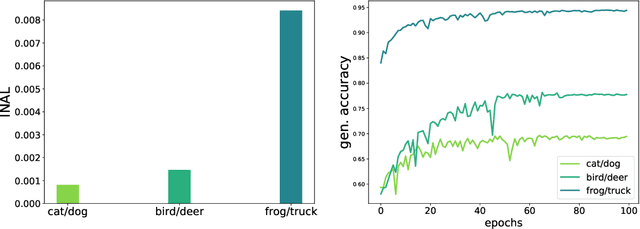
This paper introduces the notion of "Initial Alignment" (INAL) between a neural network at initialization and a target function. It is proved that if a network and target function do not have a noticeable INAL, then noisy gradient descent on a fully connected network with normalized i.i.d. initialization will not learn in polynomial time. Thus a certain amount of knowledge about the target (measured by the INAL) is needed in the architecture design. This also provides an answer to an open problem posed in [AS20]. The results are based on deriving lower-bounds for descent algorithms on symmetric neural networks without explicit knowledge of the target function beyond its INAL.

A Johnson--Lindenstrauss Framework for Randomly Initialized CNNs

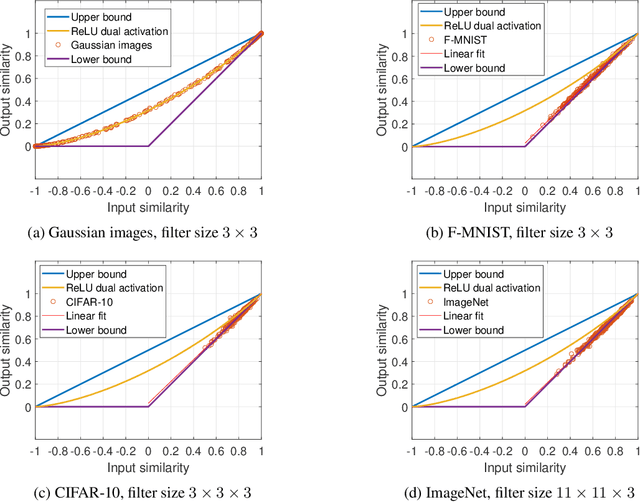
How does the geometric representation of a dataset change after the application of each randomly initialized layer of a neural network? The celebrated Johnson--Lindenstrauss lemma answers this question for linear fully-connected neural networks (FNNs), stating that the geometry is essentially preserved. For FNNs with the ReLU activation, the angle between two inputs contracts according to a known mapping. The question for non-linear convolutional neural networks (CNNs) becomes much more intricate. To answer this question, we introduce a geometric framework. For linear CNNs, we show that the Johnson--Lindenstrauss lemma continues to hold, namely, that the angle between two inputs is preserved. For CNNs with ReLU activation, on the other hand, the behavior is richer: The angle between the outputs contracts, where the level of contraction depends on the nature of the inputs. In particular, after one layer, the geometry of natural images is essentially preserved, whereas for Gaussian correlated inputs, CNNs exhibit the same contracting behavior as FNNs with ReLU activation.

Regularization by Misclassification in ReLU Neural Networks

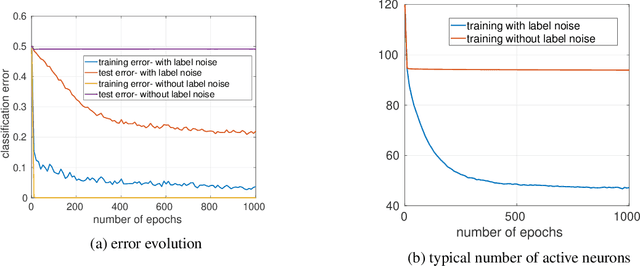
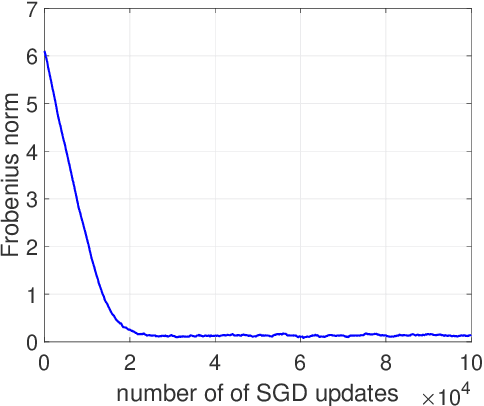
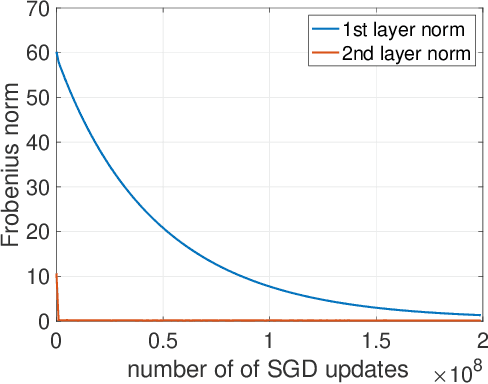
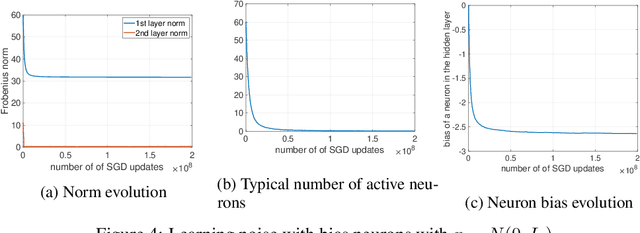
We study the implicit bias of ReLU neural networks trained by a variant of SGD where at each step, the label is changed with probability $p$ to a random label (label smoothing being a close variant of this procedure). Our experiments demonstrate that label noise propels the network to a sparse solution in the following sense: for a typical input, a small fraction of neurons are active, and the firing pattern of the hidden layers is sparser. In fact, for some instances, an appropriate amount of label noise does not only sparsify the network but further reduces the test error. We then turn to the theoretical analysis of such sparsification mechanisms, focusing on the extremal case of $p=1$. We show that in this case, the network withers as anticipated from experiments, but surprisingly, in different ways that depend on the learning rate and the presence of bias, with either weights vanishing or neurons ceasing to fire.

Bayesian Decision Making in Groups is Hard

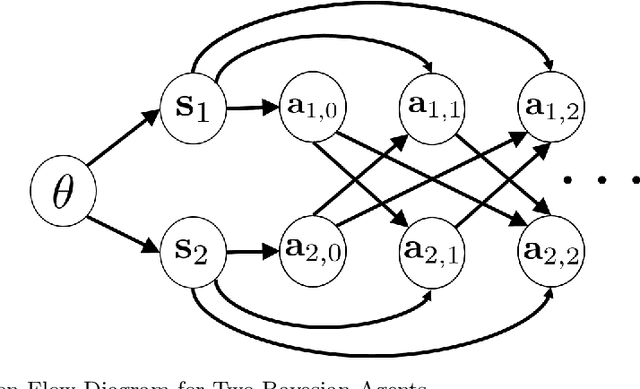
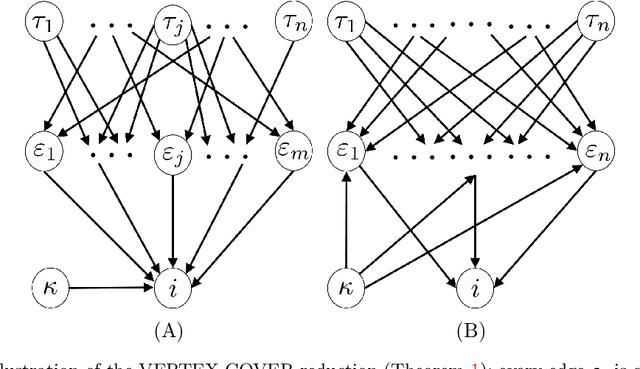
We address the computations that Bayesian agents in a network undertake in an opinion exchange model, where they repeatedly act on private information, taking myopic actions maximizing expected utility according to a fully rational posterior. We show that such computations are NP-hard for two natural utility functions, including the case where agents reveal their posteriors. Our results are robust in the sense that they show NP-hardness of distinguishing (and therefore also approximating) between posteriors that are concentrated on two distinct states of the world. We also describe a natural search algorithm that computes agents' actions, which we call iterated elimination of infeasible signals (IEIS), and show that if the network is transitive, the algorithm can be modified to run in polynomial-time.