Bayesian Decision Making in Groups is Hard

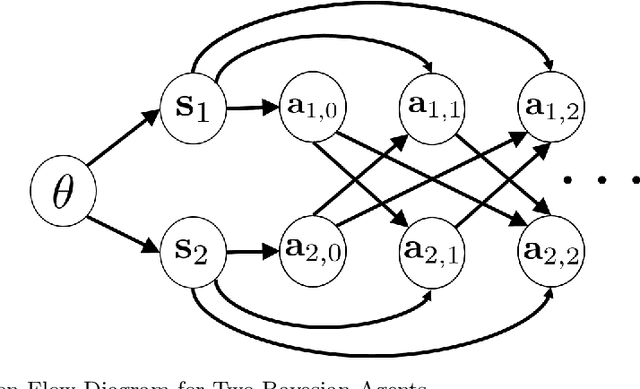
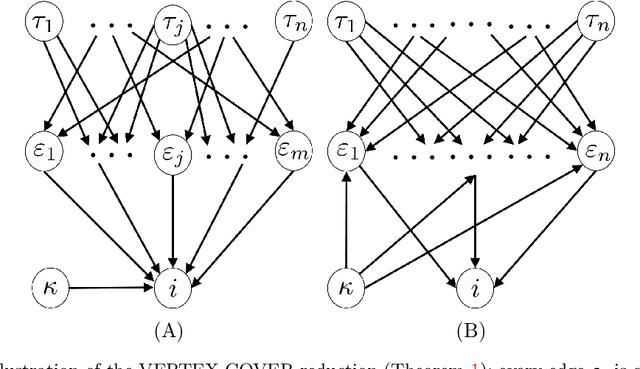
We address the computations that Bayesian agents in a network undertake in an opinion exchange model, where they repeatedly act on private information, taking myopic actions maximizing expected utility according to a fully rational posterior. We show that such computations are NP-hard for two natural utility functions, including the case where agents reveal their posteriors. Our results are robust in the sense that they show NP-hardness of distinguishing (and therefore also approximating) between posteriors that are concentrated on two distinct states of the world. We also describe a natural search algorithm that computes agents' actions, which we call iterated elimination of infeasible signals (IEIS), and show that if the network is transitive, the algorithm can be modified to run in polynomial-time.