Group Decision-Making among Privacy-Aware Agents

How can individuals exchange information to learn from each other despite their privacy needs and security concerns? For example, consider individuals deliberating a contentious topic and being concerned about divulging their private experiences. Preserving individual privacy and enabling efficient social learning are both important desiderata but seem fundamentally at odds with each other and very hard to reconcile. We do so by controlling information leakage using rigorous statistical guarantees that are based on differential privacy (DP). Our agents use log-linear rules to update their beliefs after communicating with their neighbors. Adding DP randomization noise to beliefs provides communicating agents with plausible deniability with regard to their private information and their network neighborhoods. We consider two learning environments one for distributed maximum-likelihood estimation given a finite number of private signals and another for online learning from an infinite, intermittent signal stream. Noisy information aggregation in the finite case leads to interesting tradeoffs between rejecting low-quality states and making sure all high-quality states are accepted in the algorithm output. Our results flesh out the nature of the trade-offs in both cases between the quality of the group decision outcomes, learning accuracy, communication cost, and the level of privacy protections that the agents are afforded.

Differentially Private Distributed Estimation and Learning

We study distributed estimation and learning problems in a networked environment in which agents exchange information to estimate unknown statistical properties of random variables from their privately observed samples. By exchanging information about their private observations, the agents can collectively estimate the unknown quantities, but they also face privacy risks. The goal of our aggregation schemes is to combine the observed data efficiently over time and across the network, while accommodating the privacy needs of the agents and without any coordination beyond their local neighborhoods. Our algorithms enable the participating agents to estimate a complete sufficient statistic from private signals that are acquired offline or online over time, and to preserve the privacy of their signals and network neighborhoods. This is achieved through linear aggregation schemes with adjusted randomization schemes that add noise to the exchanged estimates subject to differential privacy (DP) constraints. In every case, we demonstrate the efficiency of our algorithms by proving convergence to the estimators of a hypothetical, omniscient observer that has central access to all of the signals. We also provide convergence rate analysis and finite-time performance guarantees and show that the noise that minimizes the convergence time to the best estimates is the Laplace noise, with parameters corresponding to each agent's sensitivity to their signal and network characteristics. Finally, to supplement and validate our theoretical results, we run experiments on real-world data from the US Power Grid Network and electric consumption data from German Households to estimate the average power consumption of power stations and households under all privacy regimes.

Bayesian Decision Making in Groups is Hard

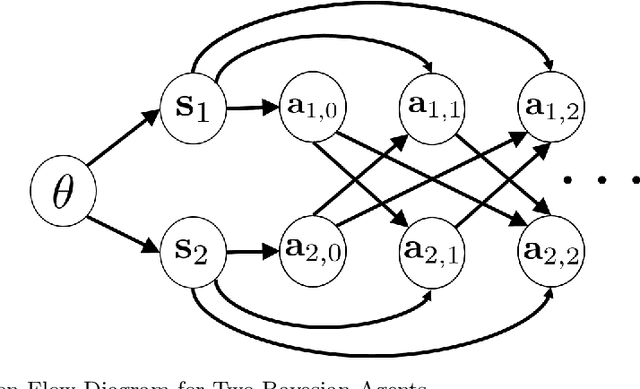
We address the computations that Bayesian agents in a network undertake in an opinion exchange model, where they repeatedly act on private information, taking myopic actions maximizing expected utility according to a fully rational posterior. We show that such computations are NP-hard for two natural utility functions, including the case where agents reveal their posteriors. Our results are robust in the sense that they show NP-hardness of distinguishing (and therefore also approximating) between posteriors that are concentrated on two distinct states of the world. We also describe a natural search algorithm that computes agents' actions, which we call iterated elimination of infeasible signals (IEIS), and show that if the network is transitive, the algorithm can be modified to run in polynomial-time.

Structural Controllability of Multi-Agent Networks: Robustness against Simultaneous Failures

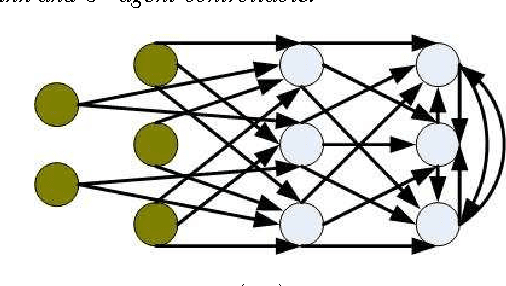
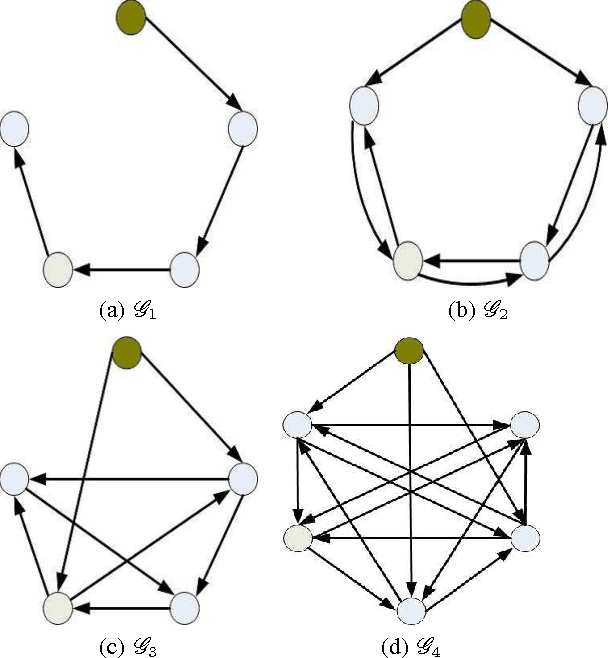
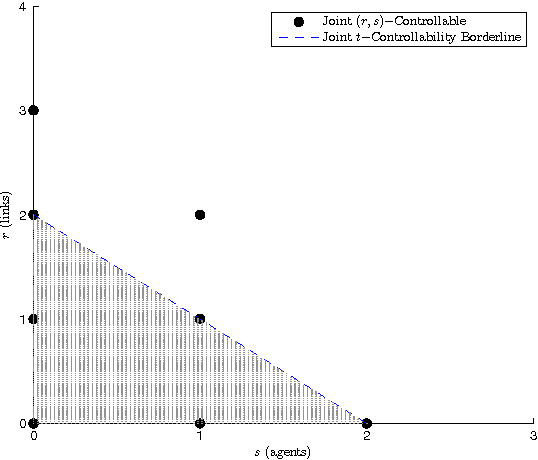
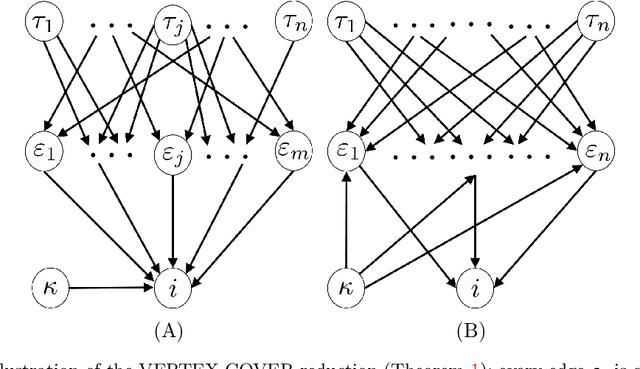
In this paper, structural controllability of a leader-follower multi-agent system with multiple leaders is studied from a graph-theoretic point of view. The problem of preservation of structural controllability under simultaneous failures in both the communication links and the agents is investigated. The effects of the loss of agents and communication links on the controllability of an information flow graph are previously studied. In this work, the corresponding results are exploited to introduce some useful indices and importance measures that help characterize and quantify the role of individual links and agents in the controllability of the overall network. Existing results are then extended by considering the effects of losses in both links and agents at the same time. To this end, the concepts of joint (r,s)-controllability and joint t-controllability are introduced as quantitative measures of reliability for a multi-agent system, and their important properties are investigated. Lastly, the class of jointly critical digraphs is introduced and it is stated that if a digraph is jointly critical, then joint t-controllability is a necessary and sufficient condition for remaining controllable following the failure of any set of links and agents, with cardinality less than t. Various examples are exploited throughout the paper to elaborate on the analytical findings.

Digraphs with Distinguishable Dynamics under the Multi-Agent Agreement Protocol

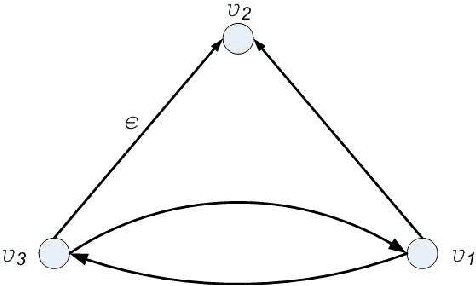
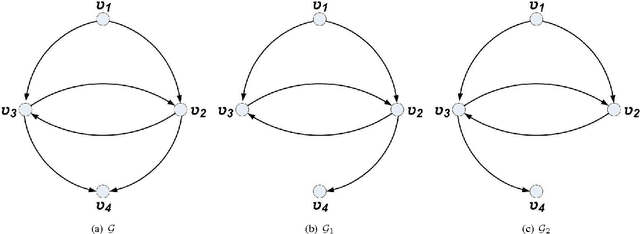
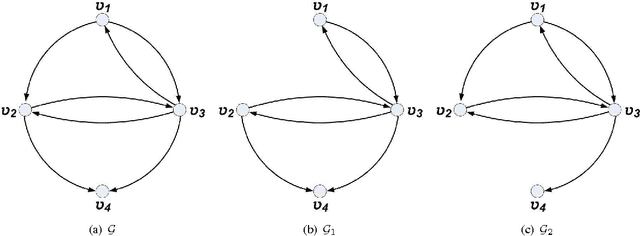
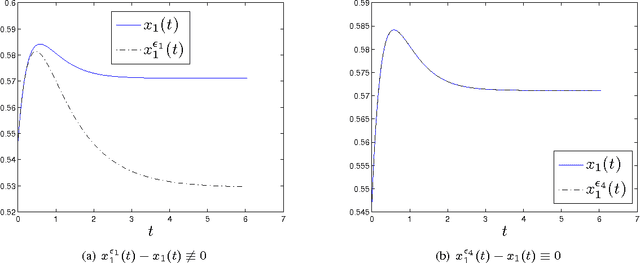
In this work, the ability to distinguish digraphs from the output response of some observing agents in a multi-agent network under the agreement protocol has been studied. Given a fixed observation point, it is desired to find sufficient graphical conditions under which the failure of a set of edges in the network information flow digraph is distinguishable from another set. When the latter is empty, this corresponds to the detectability of the former link set given the response of the observing agent. In developing the results, a powerful extension of the all-minors matrix tree theorem in algebraic graph theory is proved which relates the minors of the transformed Laplacian of a directed graph to the number and length of the shortest paths between its vertices. The results reveal an intricate relationship between the ability to distinguish the responses of a healthy and a faulty multi-agent network and the inter-nodal paths in their information flow digraphs. The results have direct implications for the operation and design of multi-agent systems subject to multiple link losses. Simulations and examples are presented to illustrate the analytic findings.

Learning without recall in directed circles and rooted trees

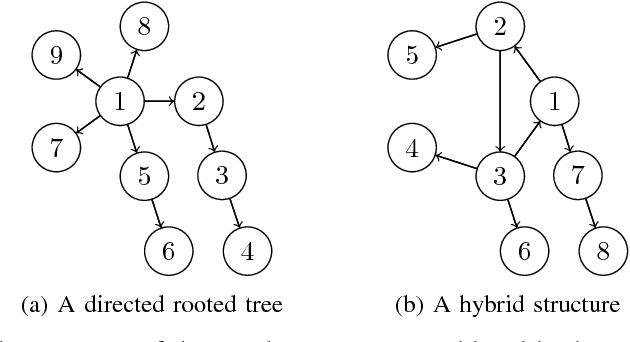
This work investigates the case of a network of agents that attempt to learn some unknown state of the world amongst the finitely many possibilities. At each time step, agents all receive random, independently distributed private signals whose distributions are dependent on the unknown state of the world. However, it may be the case that some or any of the agents cannot distinguish between two or more of the possible states based only on their private observations, as when several states result in the same distribution of the private signals. In our model, the agents form some initial belief (probability distribution) about the unknown state and then refine their beliefs in accordance with their private observations, as well as the beliefs of their neighbors. An agent learns the unknown state when her belief converges to a point mass that is concentrated at the true state. A rational agent would use the Bayes' rule to incorporate her neighbors' beliefs and own private signals over time. While such repeated applications of the Bayes' rule in networks can become computationally intractable, in this paper, we show that in the canonical cases of directed star, circle or path networks and their combinations, one can derive a class of memoryless update rules that replicate that of a single Bayesian agent but replace the self beliefs with the beliefs of the neighbors. This way, one can realize an exponentially fast rate of learning similar to the case of Bayesian (fully rational) agents. The proposed rules are a special case of the Learning without Recall.

Distributed Estimation and Learning over Heterogeneous Networks

We consider several estimation and learning problems that networked agents face when making decisions given their uncertainty about an unknown variable. Our methods are designed to efficiently deal with heterogeneity in both size and quality of the observed data, as well as heterogeneity over time (intermittence). The goal of the studied aggregation schemes is to efficiently combine the observed data that is spread over time and across several network nodes, accounting for all the network heterogeneities. Moreover, we require no form of coordination beyond the local neighborhood of every network agent or sensor node. The three problems that we consider are (i) maximum likelihood estimation of the unknown given initial data sets, (ii) learning the true model parameter from streams of data that the agents receive intermittently over time, and (iii) minimum variance estimation of a complete sufficient statistic from several data points that the networked agents collect over time. In each case we rely on an aggregation scheme to combine the observations of all agents; moreover, when the agents receive streams of data over time, we modify the update rules to accommodate the most recent observations. In every case, we demonstrate the efficiency of our algorithms by proving convergence to the globally efficient estimators given the observations of all agents. We supplement these results by investigating the rate of convergence and providing finite-time performance guarantees.