Structural Controllability of Multi-Agent Networks: Robustness against Simultaneous Failures

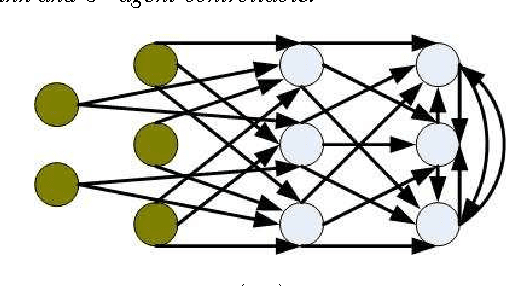
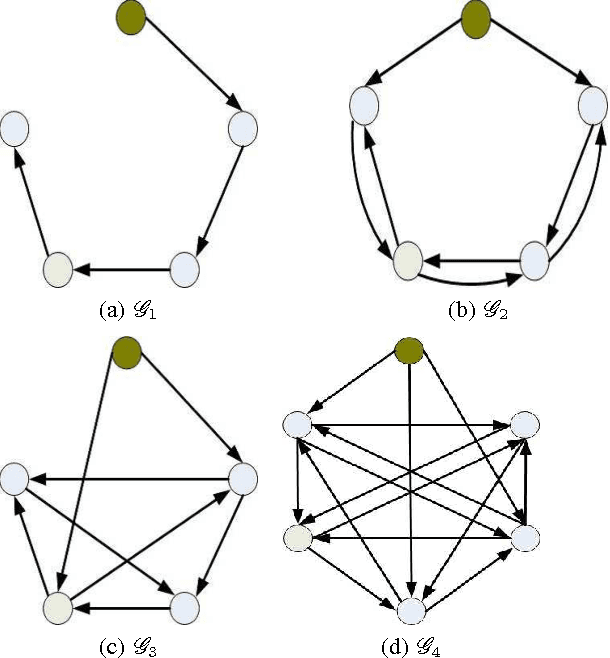
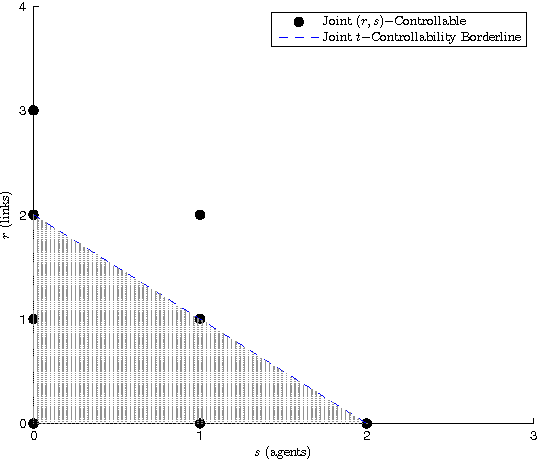
In this paper, structural controllability of a leader-follower multi-agent system with multiple leaders is studied from a graph-theoretic point of view. The problem of preservation of structural controllability under simultaneous failures in both the communication links and the agents is investigated. The effects of the loss of agents and communication links on the controllability of an information flow graph are previously studied. In this work, the corresponding results are exploited to introduce some useful indices and importance measures that help characterize and quantify the role of individual links and agents in the controllability of the overall network. Existing results are then extended by considering the effects of losses in both links and agents at the same time. To this end, the concepts of joint (r,s)-controllability and joint t-controllability are introduced as quantitative measures of reliability for a multi-agent system, and their important properties are investigated. Lastly, the class of jointly critical digraphs is introduced and it is stated that if a digraph is jointly critical, then joint t-controllability is a necessary and sufficient condition for remaining controllable following the failure of any set of links and agents, with cardinality less than t. Various examples are exploited throughout the paper to elaborate on the analytical findings.