Digraphs with Distinguishable Dynamics under the Multi-Agent Agreement Protocol
Paper and Code
Nov 30, 2016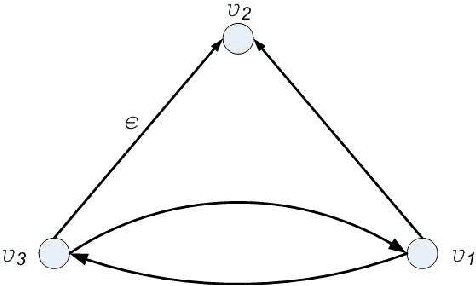
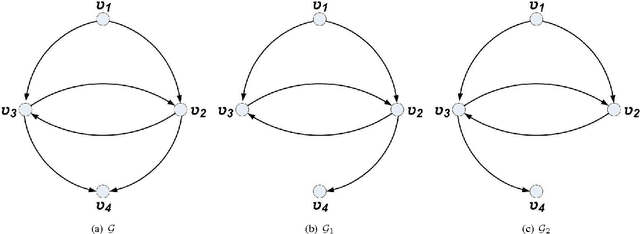
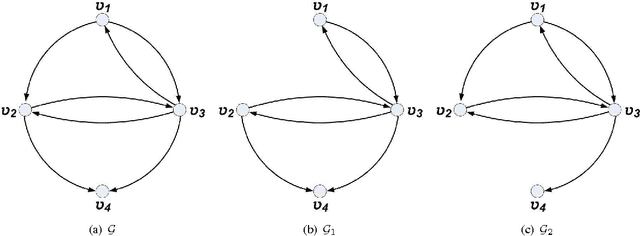
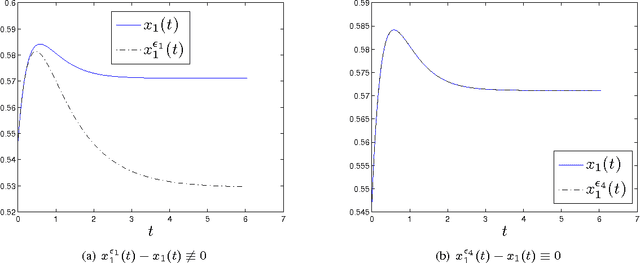
In this work, the ability to distinguish digraphs from the output response of some observing agents in a multi-agent network under the agreement protocol has been studied. Given a fixed observation point, it is desired to find sufficient graphical conditions under which the failure of a set of edges in the network information flow digraph is distinguishable from another set. When the latter is empty, this corresponds to the detectability of the former link set given the response of the observing agent. In developing the results, a powerful extension of the all-minors matrix tree theorem in algebraic graph theory is proved which relates the minors of the transformed Laplacian of a directed graph to the number and length of the shortest paths between its vertices. The results reveal an intricate relationship between the ability to distinguish the responses of a healthy and a faulty multi-agent network and the inter-nodal paths in their information flow digraphs. The results have direct implications for the operation and design of multi-agent systems subject to multiple link losses. Simulations and examples are presented to illustrate the analytic findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge