On the Role of Attention Masks and LayerNorm in Transformers

Self-attention is the key mechanism of transformers, which are the essential building blocks of modern foundation models. Recent studies have shown that pure self-attention suffers from an increasing degree of rank collapse as depth increases, limiting model expressivity and further utilization of model depth. The existing literature on rank collapse, however, has mostly overlooked other critical components in transformers that may alleviate the rank collapse issue. In this paper, we provide a general analysis of rank collapse under self-attention, taking into account the effects of attention masks and layer normalization (LayerNorm). In particular, we find that although pure masked attention still suffers from exponential collapse to a rank one subspace, local masked attention can provably slow down the collapse rate. In the case of self-attention with LayerNorm, we first show that for certain classes of value matrices, collapse to a rank one subspace still happens exponentially. However, through construction of nontrivial counterexamples, we then establish that with proper choice of value matrices, a general class of sequences may not converge to a rank one subspace, and the self-attention dynamics with LayerNorm can simultaneously possess a rich set of equilibria with any possible rank between one and full. Our result refutes the previous hypothesis that LayerNorm plays no role in the rank collapse of self-attention and suggests that self-attention with LayerNorm constitutes a much more expressive, versatile nonlinear dynamical system than what was originally thought.

Belief Samples Are All You Need For Social Learning

In this paper, we consider the problem of social learning, where a group of agents embedded in a social network are interested in learning an underlying state of the world. Agents have incomplete, noisy, and heterogeneous sources of information, providing them with recurring private observations of the underlying state of the world. Agents can share their learning experience with their peers by taking actions observable to them, with values from a finite feasible set of states. Actions can be interpreted as samples from the beliefs which agents may form and update on what the true state of the world is. Sharing samples, in place of full beliefs, is motivated by the limited communication, cognitive, and information-processing resources available to agents especially in large populations. Previous work (Salhab et al.) poses the question as to whether learning with probability one is still achievable if agents are only allowed to communicate samples from their beliefs. We provide a definite positive answer to this question, assuming a strongly connected network and a ``collective distinguishability'' assumption, which are both required for learning even in full-belief-sharing settings. In our proposed belief update mechanism, each agent's belief is a normalized weighted geometric interpolation between a fully Bayesian private belief -- aggregating information from the private source -- and an ensemble of empirical distributions of the samples shared by her neighbors over time. By carefully constructing asymptotic almost-sure lower/upper bounds on the frequency of shared samples matching the true state/or not, we rigorously prove the convergence of all the beliefs to the true state, with probability one.

Demystifying Oversmoothing in Attention-Based Graph Neural Networks

Oversmoothing in Graph Neural Networks (GNNs) refers to the phenomenon where increasing network depth leads to homogeneous node representations. While previous work has established that Graph Convolutional Networks (GCNs) exponentially lose expressive power, it remains controversial whether the graph attention mechanism can mitigate oversmoothing. In this work, we provide a definitive answer to this question through a rigorous mathematical analysis, by viewing attention-based GNNs as nonlinear time-varying dynamical systems and incorporating tools and techniques from the theory of products of inhomogeneous matrices and the joint spectral radius. We establish that, contrary to popular belief, the graph attention mechanism cannot prevent oversmoothing and loses expressive power exponentially. The proposed framework extends the existing results on oversmoothing for symmetric GCNs to a significantly broader class of GNN models. In particular, our analysis accounts for asymmetric, state-dependent and time-varying aggregation operators and a wide range of common nonlinear activation functions, such as ReLU, LeakyReLU, GELU and SiLU.

Digraphs with Distinguishable Dynamics under the Multi-Agent Agreement Protocol

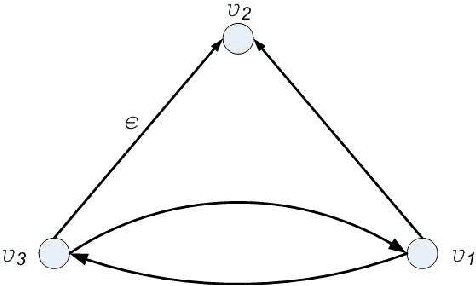
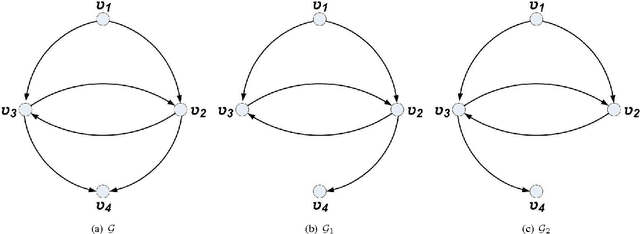
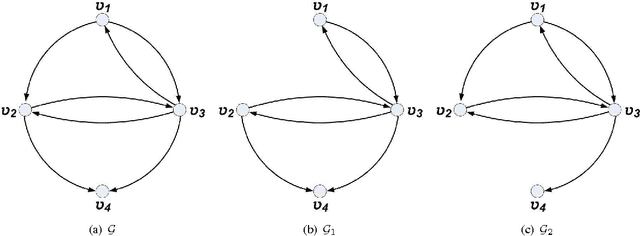
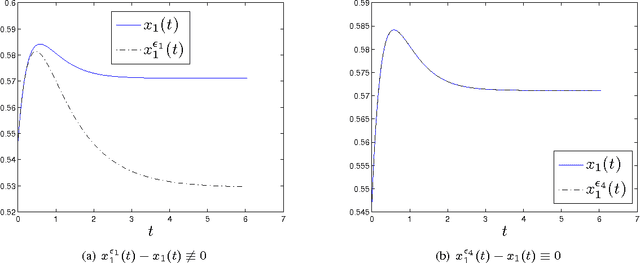
In this work, the ability to distinguish digraphs from the output response of some observing agents in a multi-agent network under the agreement protocol has been studied. Given a fixed observation point, it is desired to find sufficient graphical conditions under which the failure of a set of edges in the network information flow digraph is distinguishable from another set. When the latter is empty, this corresponds to the detectability of the former link set given the response of the observing agent. In developing the results, a powerful extension of the all-minors matrix tree theorem in algebraic graph theory is proved which relates the minors of the transformed Laplacian of a directed graph to the number and length of the shortest paths between its vertices. The results reveal an intricate relationship between the ability to distinguish the responses of a healthy and a faulty multi-agent network and the inter-nodal paths in their information flow digraphs. The results have direct implications for the operation and design of multi-agent systems subject to multiple link losses. Simulations and examples are presented to illustrate the analytic findings.