Regularization by Misclassification in ReLU Neural Networks
Paper and Code
Nov 03, 2021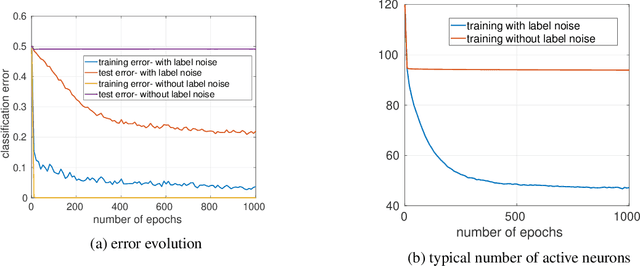
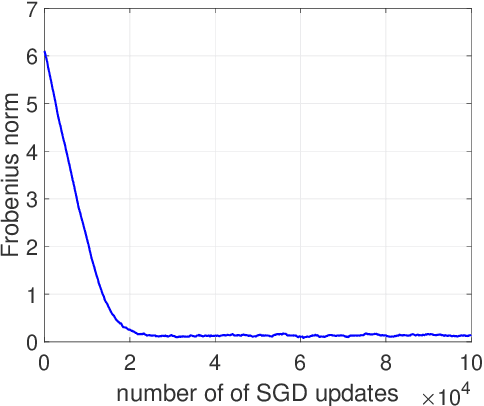
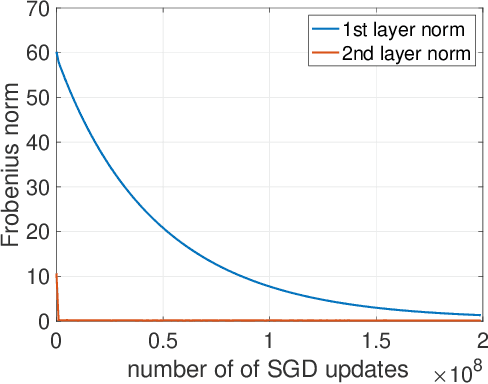
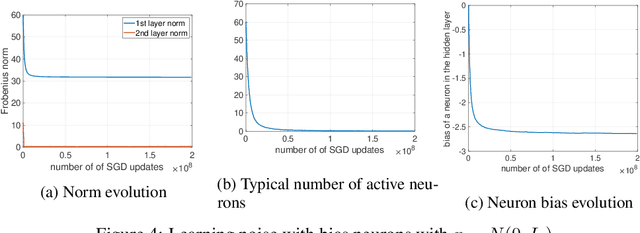
We study the implicit bias of ReLU neural networks trained by a variant of SGD where at each step, the label is changed with probability $p$ to a random label (label smoothing being a close variant of this procedure). Our experiments demonstrate that label noise propels the network to a sparse solution in the following sense: for a typical input, a small fraction of neurons are active, and the firing pattern of the hidden layers is sparser. In fact, for some instances, an appropriate amount of label noise does not only sparsify the network but further reduces the test error. We then turn to the theoretical analysis of such sparsification mechanisms, focusing on the extremal case of $p=1$. We show that in this case, the network withers as anticipated from experiments, but surprisingly, in different ways that depend on the learning rate and the presence of bias, with either weights vanishing or neurons ceasing to fire.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge