What One Cannot, Two Can: Two-Layer Transformers Provably Represent Induction Heads on Any-Order Markov Chains

In-context learning (ICL) is a hallmark capability of transformers, through which trained models learn to adapt to new tasks by leveraging information from the input context. Prior work has shown that ICL emerges in transformers due to the presence of special circuits called induction heads. Given the equivalence between induction heads and conditional k-grams, a recent line of work modeling sequential inputs as Markov processes has revealed the fundamental impact of model depth on its ICL capabilities: while a two-layer transformer can efficiently represent a conditional 1-gram model, its single-layer counterpart cannot solve the task unless it is exponentially large. However, for higher order Markov sources, the best known constructions require at least three layers (each with a single attention head) - leaving open the question: can a two-layer single-head transformer represent any kth-order Markov process? In this paper, we precisely address this and theoretically show that a two-layer transformer with one head per layer can indeed represent any conditional k-gram. Thus, our result provides the tightest known characterization of the interplay between transformer depth and Markov order for ICL. Building on this, we further analyze the learning dynamics of our two-layer construction, focusing on a simplified variant for first-order Markov chains, illustrating how effective in-context representations emerge during training. Together, these results deepen our current understanding of transformer-based ICL and illustrate how even shallow architectures can surprisingly exhibit strong ICL capabilities on structured sequence modeling tasks.

PuzzleWorld: A Benchmark for Multimodal, Open-Ended Reasoning in Puzzlehunts

Puzzlehunts are a genre of complex, multi-step puzzles lacking well-defined problem definitions. In contrast to conventional reasoning benchmarks consisting of tasks with clear instructions, puzzlehunts require models to discover the underlying problem structure from multimodal evidence and iterative reasoning, mirroring real-world domains such as scientific discovery, exploratory data analysis, or investigative problem-solving. Despite recent progress in foundation models, their performance on such open-ended settings remains largely untested. In this paper, we introduce PuzzleWorld, a large-scale benchmark of 667 puzzlehunt-style problems designed to assess step-by-step, open-ended, and creative multimodal reasoning. Each puzzle is annotated with the final solution, detailed reasoning traces, and cognitive skill labels, enabling holistic benchmarking and fine-grained diagnostic analysis. Most state-of-the-art models achieve only 1-2% final answer accuracy, with the best model solving only 14% of puzzles and reaching 40% stepwise accuracy. To demonstrate the value of our reasoning annotations, we show that fine-tuning a small model on reasoning traces improves stepwise reasoning from 4% to 11%, while training on final answers alone degrades performance to near zero. Our error analysis reveals that current models exhibit myopic reasoning, are bottlenecked by the limitations of language-based inference, and lack sketching capabilities crucial for visual and spatial reasoning. We release PuzzleWorld at https://github.com/MIT-MI/PuzzleWorld to support future work on building more general, open-ended, and creative reasoning systems.

TAMP: Token-Adaptive Layerwise Pruning in Multimodal Large Language Models

Multimodal Large Language Models (MLLMs) have shown remarkable versatility in understanding diverse multimodal data and tasks. However, these capabilities come with an increased model scale. While post-training pruning reduces model size in unimodal models, its application to MLLMs often yields limited success. Our analysis discovers that conventional methods fail to account for the unique token attributes across layers and modalities inherent to MLLMs. Inspired by this observation, we propose TAMP, a simple yet effective pruning framework tailored for MLLMs, featuring two key components: (1) Diversity-Aware Sparsity, which adjusts sparsity ratio per layer based on diversities among multimodal output tokens, preserving more parameters in high-diversity layers; and (2) Adaptive Multimodal Input Activation, which identifies representative multimodal input tokens using attention scores to guide unstructured weight pruning. We validate our method on two state-of-the-art MLLMs: LLaVA-NeXT, designed for vision-language tasks, and VideoLLaMA2, capable of processing audio, visual, and language modalities. Empirical experiments across various multimodal evaluation benchmarks demonstrate that each component of our approach substantially outperforms existing pruning techniques.

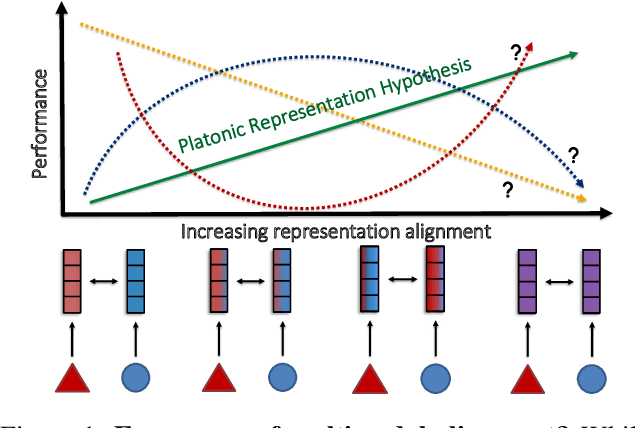
Understanding the Emergence of Multimodal Representation Alignment

Multimodal representation learning is fundamentally about transforming incomparable modalities into comparable representations. While prior research primarily focused on explicitly aligning these representations through targeted learning objectives and model architectures, a recent line of work has found that independently trained unimodal models of increasing scale and performance can become implicitly aligned with each other. These findings raise fundamental questions regarding the emergence of aligned representations in multimodal learning. Specifically: (1) when and why does alignment emerge implicitly? and (2) is alignment a reliable indicator of performance? Through a comprehensive empirical investigation, we demonstrate that both the emergence of alignment and its relationship with task performance depend on several critical data characteristics. These include, but are not necessarily limited to, the degree of similarity between the modalities and the balance between redundant and unique information they provide for the task. Our findings suggest that alignment may not be universally beneficial; rather, its impact on performance varies depending on the dataset and task. These insights can help practitioners determine whether increasing alignment between modalities is advantageous or, in some cases, detrimental to achieving optimal performance. Code is released at https://github.com/MeganTj/multimodal_alignment.

Local to Global: Learning Dynamics and Effect of Initialization for Transformers

In recent years, transformer-based models have revolutionized deep learning, particularly in sequence modeling. To better understand this phenomenon, there is a growing interest in using Markov input processes to study transformers. However, our current understanding in this regard remains limited with many fundamental questions about how transformers learn Markov chains still unanswered. In this paper, we address this by focusing on first-order Markov chains and single-layer transformers, providing a comprehensive characterization of the learning dynamics in this context. Specifically, we prove that transformer parameters trained on next-token prediction loss can either converge to global or local minima, contingent on the initialization and the Markovian data properties, and we characterize the precise conditions under which this occurs. To the best of our knowledge, this is the first result of its kind highlighting the role of initialization. We further demonstrate that our theoretical findings are corroborated by empirical evidence. Based on these insights, we provide guidelines for the initialization of transformer parameters and demonstrate their effectiveness. Finally, we outline several open problems in this arena. Code is available at: \url{https://anonymous.4open.science/r/Local-to-Global-C70B/}.

FiGURe: Simple and Efficient Unsupervised Node Representations with Filter Augmentations

Unsupervised node representations learnt using contrastive learning-based methods have shown good performance on downstream tasks. However, these methods rely on augmentations that mimic low-pass filters, limiting their performance on tasks requiring different eigen-spectrum parts. This paper presents a simple filter-based augmentation method to capture different parts of the eigen-spectrum. We show significant improvements using these augmentations. Further, we show that sharing the same weights across these different filter augmentations is possible, reducing the computational load. In addition, previous works have shown that good performance on downstream tasks requires high dimensional representations. Working with high dimensions increases the computations, especially when multiple augmentations are involved. We mitigate this problem and recover good performance through lower dimensional embeddings using simple random Fourier feature projections. Our method, FiGURe achieves an average gain of up to 4.4%, compared to the state-of-the-art unsupervised models, across all datasets in consideration, both homophilic and heterophilic. Our code can be found at: https://github.com/microsoft/figure.

Consistent Training via Energy-Based GFlowNets for Modeling Discrete Joint Distributions

Generative Flow Networks (GFlowNets) have demonstrated significant performance improvements for generating diverse discrete objects $x$ given a reward function $R(x)$, indicating the utility of the object and trained independently from the GFlowNet by supervised learning to predict a desirable property $y$ given $x$. We hypothesize that this can lead to incompatibility between the inductive optimization biases in training $R$ and in training the GFlowNet, potentially leading to worse samples and slow adaptation to changes in the distribution. In this work, we build upon recent work on jointly learning energy-based models with GFlowNets and extend it to learn the joint over multiple variables, which we call Joint Energy-Based GFlowNets (JEBGFNs), such as peptide sequences and their antimicrobial activity. Joint learning of the energy-based model, used as a reward for the GFlowNet, can resolve the issues of incompatibility since both the reward function $R$ and the GFlowNet sampler are trained jointly. We find that this joint training or joint energy-based formulation leads to significant improvements in generating anti-microbial peptides. As the training sequences arose out of evolutionary or artificial selection for high antibiotic activity, there is presumably some structure in the distribution of sequences that reveals information about the antibiotic activity. This results in an advantage to modeling their joint generatively vs. pure discriminative modeling. We also evaluate JEBGFN in an active learning setting for discovering anti-microbial peptides.

Biological Sequence Design with GFlowNets

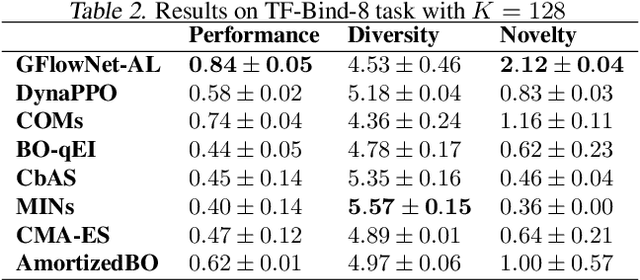
Design of de novo biological sequences with desired properties, like protein and DNA sequences, often involves an active loop with several rounds of molecule ideation and expensive wet-lab evaluations. These experiments can consist of multiple stages, with increasing levels of precision and cost of evaluation, where candidates are filtered. This makes the diversity of proposed candidates a key consideration in the ideation phase. In this work, we propose an active learning algorithm leveraging epistemic uncertainty estimation and the recently proposed GFlowNets as a generator of diverse candidate solutions, with the objective to obtain a diverse batch of useful (as defined by some utility function, for example, the predicted anti-microbial activity of a peptide) and informative candidates after each round. We also propose a scheme to incorporate existing labeled datasets of candidates, in addition to a reward function, to speed up learning in GFlowNets. We present empirical results on several biological sequence design tasks, and we find that our method generates more diverse and novel batches with high scoring candidates compared to existing approaches.

A Piece-wise Polynomial Filtering Approach for Graph Neural Networks

Graph Neural Networks (GNNs) exploit signals from node features and the input graph topology to improve node classification task performance. However, these models tend to perform poorly on heterophilic graphs, where connected nodes have different labels. Recently proposed GNNs work across graphs having varying levels of homophily. Among these, models relying on polynomial graph filters have shown promise. We observe that solutions to these polynomial graph filter models are also solutions to an overdetermined system of equations. It suggests that in some instances, the model needs to learn a reasonably high order polynomial. On investigation, we find the proposed models ineffective at learning such polynomials due to their designs. To mitigate this issue, we perform an eigendecomposition of the graph and propose to learn multiple adaptive polynomial filters acting on different subsets of the spectrum. We theoretically and empirically show that our proposed model learns a better filter, thereby improving classification accuracy. We study various aspects of our proposed model including, dependency on the number of eigencomponents utilized, latent polynomial filters learned, and performance of the individual polynomials on the node classification task. We further show that our model is scalable by evaluating over large graphs. Our model achieves performance gains of up to 5% over the state-of-the-art models and outperforms existing polynomial filter-based approaches in general.