Information-theoretic signatures of causality in Bayesian networks and hypergraphs

Analyzing causality in multivariate systems involves establishing how information is generated, distributed and combined, and thus requires tools that capture interactions beyond pairwise relations. Higher-order information theory provides such tools. In particular, Partial Information Decomposition (PID) allows the decomposition of the information that a set of sources provides about a target into redundant, unique, and synergistic components. Yet the mathematical connection between such higher-order information-theoretic measures and causal structure remains undeveloped. Here we establish the first theoretical correspondence between PID components and causal structure in both Bayesian networks and hypergraphs. We first show that in Bayesian networks unique information precisely characterizes direct causal neighbors, while synergy identifies collider relationships. This establishes a localist causal discovery paradigm in which the structure surrounding each variable can be recovered from its immediate informational footprint, eliminating the need for global search over graph space. Extending these results to higher-order systems, we prove that PID signatures in Bayesian hypergraphs differentiate parents, children, co-heads, and co-tails, revealing a higher-order collider effect unique to multi-tail hyperedges. We also present procedures by which our results can be used to characterize systematically the causal structure of Bayesian networks and hypergraphs. Our results position PID as a rigorous, model-agnostic foundation for inferring both pairwise and higher-order causal structure, and introduce a fundamentally local information-theoretic viewpoint on causal discovery.

Protein generation with embedding learning for motif diversification

A fundamental challenge in protein design is the trade-off between generating structural diversity while preserving motif biological function. Current state-of-the-art methods, such as partial diffusion in RFdiffusion, often fail to resolve this trade-off: small perturbations yield motifs nearly identical to the native structure, whereas larger perturbations violate the geometric constraints necessary for biological function. We introduce Protein Generation with Embedding Learning (PGEL), a general framework that learns high-dimensional embeddings encoding sequence and structural features of a target motif in the representation space of a diffusion model's frozen denoiser, and then enhances motif diversity by introducing controlled perturbations in the embedding space. PGEL is thus able to loosen geometric constraints while satisfying typical design metrics, leading to more diverse yet viable structures. We demonstrate PGEL on three representative cases: a monomer, a protein-protein interface, and a cancer-related transcription factor complex. In all cases, PGEL achieves greater structural diversity, better designability, and improved self-consistency, as compared to partial diffusion. Our results establish PGEL as a general strategy for embedding-driven protein generation allowing for systematic, viable diversification of functional motifs.

Permutation-Free High-Order Interaction Tests

Kernel-based hypothesis tests offer a flexible, non-parametric tool to detect high-order interactions in multivariate data, beyond pairwise relationships. Yet the scalability of such tests is limited by the computationally demanding permutation schemes used to generate null approximations. Here we introduce a family of permutation-free high-order tests for joint independence and partial factorisations of $d$ variables. Our tests eliminate the need for permutation-based approximations by leveraging V-statistics and a novel cross-centring technique to yield test statistics with a standard normal limiting distribution under the null. We present implementations of the tests and showcase their efficacy and scalability through synthetic datasets. We also show applications inspired by causal discovery and feature selection, which highlight both the importance of high-order interactions in data and the need for efficient computational methods.

Information-Theoretic Measures on Lattices for High-Order Interactions

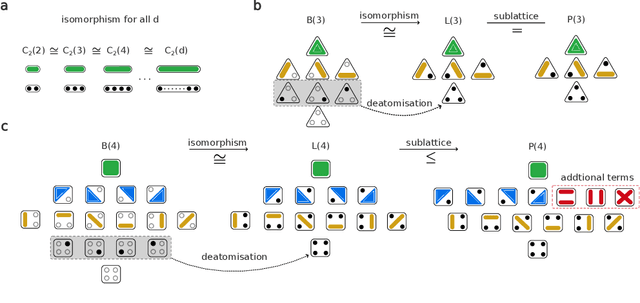
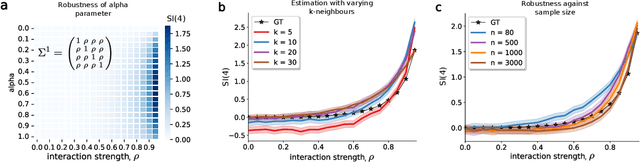
Traditional models reliant solely on pairwise associations often prove insufficient in capturing the complex statistical structure inherent in multivariate data. Yet existing methods for identifying information shared among groups of $d>3$ variables are often intractable; asymmetric around a target variable; or unable to consider all factorisations of the joint probability distribution. Here, we present a framework that systematically derives high-order measures using lattice and operator function pairs, whereby the lattice captures the algebraic relational structure of the variables and the operator function computes measures over the lattice. We show that many existing information-theoretic high-order measures can be derived by using divergences as operator functions on sublattices of the partition lattice, thus preventing the accurate quantification of all interactions for $d>3$. Similarly, we show that using the KL divergence as the operator function also leads to unwanted cancellation of interactions for $d>3$. To characterise all interactions among $d$ variables, we introduce the Streitberg information defined on the full partition lattice using generalisations of the KL divergence as operator functions. We validate our results numerically on synthetic data, and illustrate the use of the Streitberg information through applications to stock market returns and neural electrophysiology data.

LGDE: Local Graph-based Dictionary Expansion

Expanding a dictionary of pre-selected keywords is crucial for tasks in information retrieval, such as database query and online data collection. Here we propose Local Graph-based Dictionary Expansion (LGDE), a method that uses tools from manifold learning and network science for the data-driven discovery of keywords starting from a seed dictionary. At the heart of LGDE lies the creation of a word similarity graph derived from word embeddings and the application of local community detection based on graph diffusion to discover semantic neighbourhoods of pre-defined seed keywords. The diffusion in the local graph manifold allows the exploration of the complex nonlinear geometry of word embeddings and can capture word similarities based on paths of semantic association. We validate our method on a corpus of hate speech-related posts from Reddit and Gab and show that LGDE enriches the list of keywords and achieves significantly better performance than threshold methods based on direct word similarities. We further demonstrate the potential of our method through a real-world use case from communication science, where LGDE is evaluated quantitatively on data collected and analysed by domain experts by expanding a conspiracy-related dictionary.

Hyperspectral unmixing for Raman spectroscopy via physics-constrained autoencoders

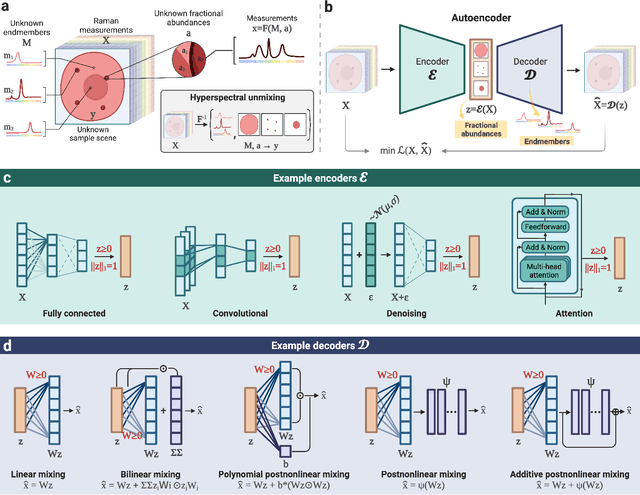
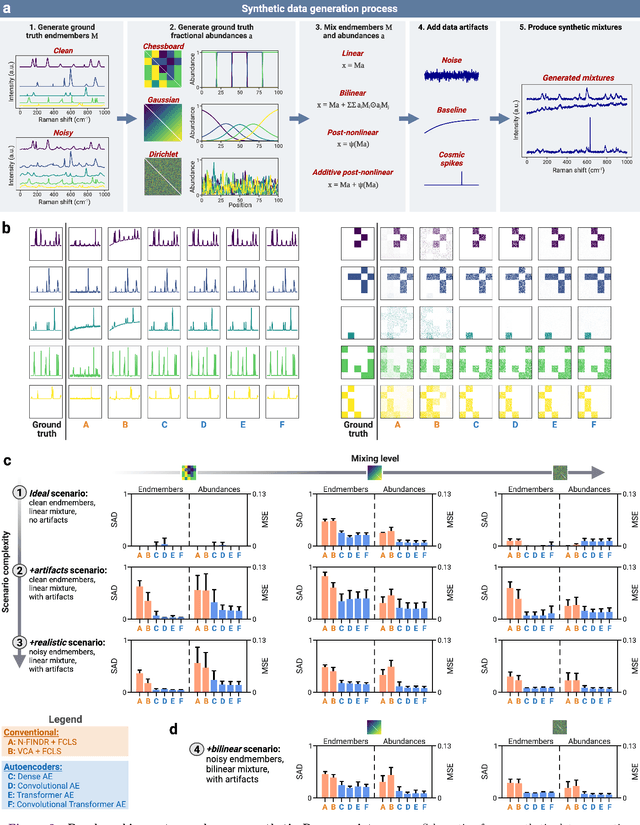
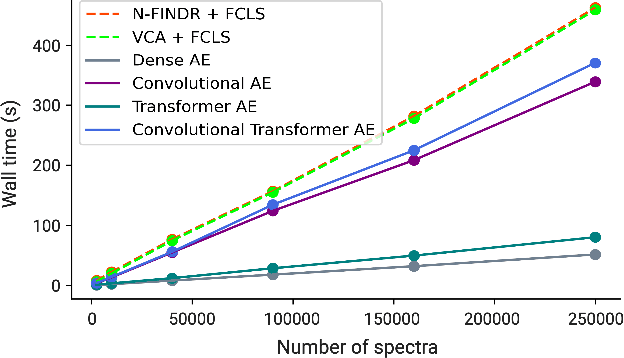
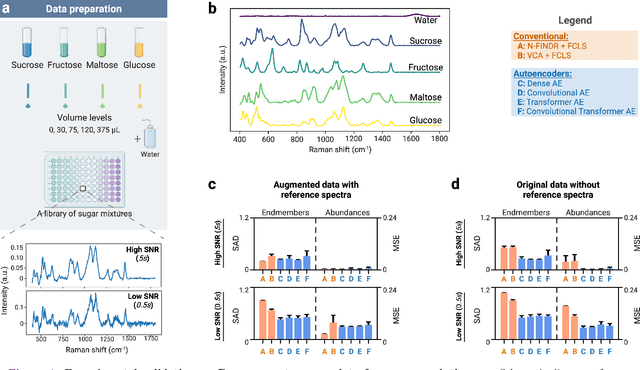
Raman spectroscopy is widely used across scientific domains to characterize the chemical composition of samples in a non-destructive, label-free manner. Many applications entail the unmixing of signals from mixtures of molecular species to identify the individual components present and their proportions, yet conventional methods for chemometrics often struggle with complex mixture scenarios encountered in practice. Here, we develop hyperspectral unmixing algorithms based on autoencoder neural networks, and we systematically validate them using both synthetic and experimental benchmark datasets created in-house. Our results demonstrate that unmixing autoencoders provide improved accuracy, robustness and efficiency compared to standard unmixing methods. We also showcase the applicability of autoencoders to complex biological settings by showing improved biochemical characterization of volumetric Raman imaging data from a monocytic cell.

A continuous Structural Intervention Distance to compare Causal Graphs

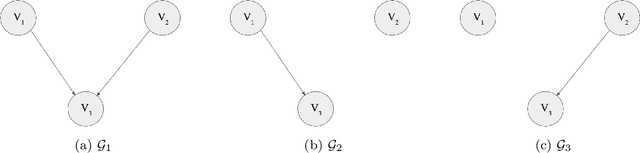
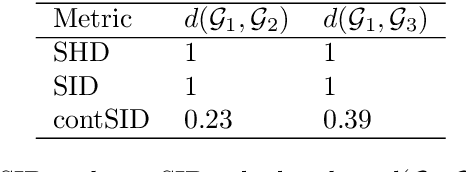
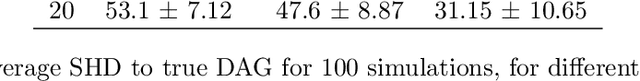
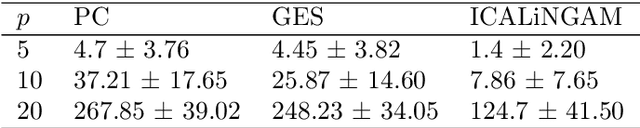
Understanding and adequately assessing the difference between a true and a learnt causal graphs is crucial for causal inference under interventions. As an extension to the graph-based structural Hamming distance and structural intervention distance, we propose a novel continuous-measured metric that considers the underlying data in addition to the graph structure for its calculation of the difference between a true and a learnt causal graph. The distance is based on embedding intervention distributions over each pair of nodes as conditional mean embeddings into reproducing kernel Hilbert spaces and estimating their difference by the maximum (conditional) mean discrepancy. We show theoretical results which we validate with numerical experiments on synthetic data.

Interaction Measures, Partition Lattices and Kernel Tests for High-Order Interactions

Models that rely solely on pairwise relationships often fail to capture the complete statistical structure of the complex multivariate data found in diverse domains, such as socio-economic, ecological, or biomedical systems. Non-trivial dependencies between groups of more than two variables can play a significant role in the analysis and modelling of such systems, yet extracting such high-order interactions from data remains challenging. Here, we introduce a hierarchy of $d$-order ($d \geq 2$) interaction measures, increasingly inclusive of possible factorisations of the joint probability distribution, and define non-parametric, kernel-based tests to establish systematically the statistical significance of $d$-order interactions. We also establish mathematical links with lattice theory, which elucidate the derivation of the interaction measures and their composite permutation tests; clarify the connection of simplicial complexes with kernel matrix centring; and provide a means to enhance computational efficiency. We illustrate our results numerically with validations on synthetic data, and through an application to neuroimaging data.

Kernel-based Joint Independence Tests for Multivariate Stationary and Nonstationary Time-Series

Multivariate time-series data that capture the temporal evolution of interconnected systems are ubiquitous in diverse areas. Understanding the complex relationships and potential dependencies among co-observed variables is crucial for the accurate statistical modelling and analysis of such systems. Here, we introduce kernel-based statistical tests of joint independence in multivariate time-series by extending the d-variable Hilbert-Schmidt independence criterion (dHSIC) to encompass both stationary and nonstationary random processes, thus allowing broader real-world applications. By leveraging resampling techniques tailored for both single- and multiple-realization time series, we show how the method robustly uncovers significant higher-order dependencies in synthetic examples, including frequency mixing data, as well as real-world climate and socioeconomic data. Our method adds to the mathematical toolbox for the analysis of complex high-dimensional time-series datasets.

Persistent Homology of the Multiscale Clustering Filtration

In many applications in data clustering, it is desirable to find not just a single partition but a sequence of partitions that describes the data at different scales, or levels of coarseness, leading naturally to Sankey diagrams as descriptors of the data. The problem of multiscale clustering then becomes how to to select robust intrinsic scales, and how to analyse and compare the (not necessarily hierarchical) sequences of partitions. Here, we define a novel filtration, the Multiscale Clustering Filtration (MCF), which encodes arbitrary patterns of cluster assignments across scales. We prove that the MCF is a proper filtration, give an equivalent construction via nerves, and show that in the hierarchical case the MCF reduces to the Vietoris-Rips filtration of an ultrametric space. We also show that the zero-dimensional persistent homology of the MCF provides a measure of the level of hierarchy in the sequence of partitions, whereas the higher-dimensional persistent homology tracks the emergence and resolution of conflicts between cluster assignments across scales. We briefly illustrate numerically how the structure of the persistence diagram can serve to characterise multiscale data clusterings.