Interpretable statistical representations of neural population dynamics and geometry

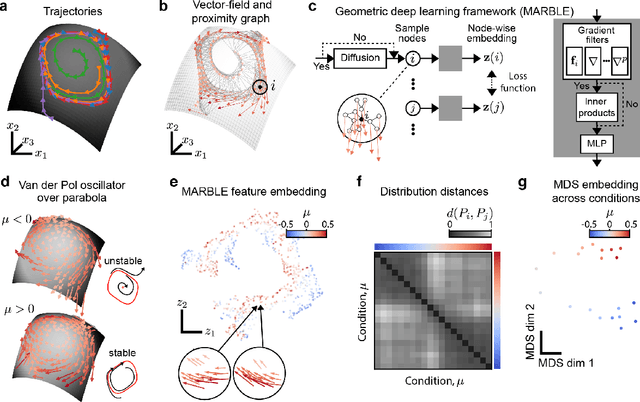
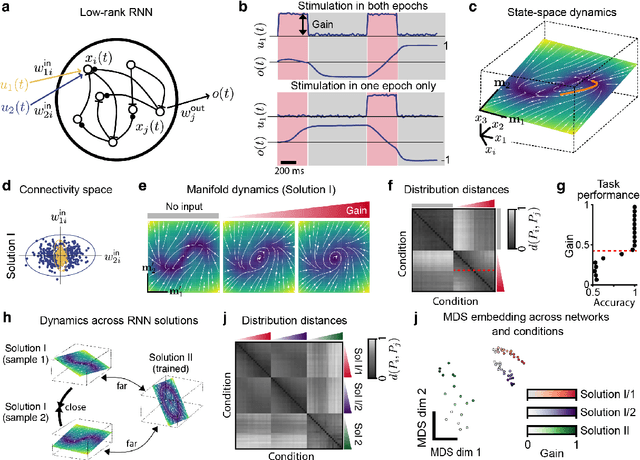
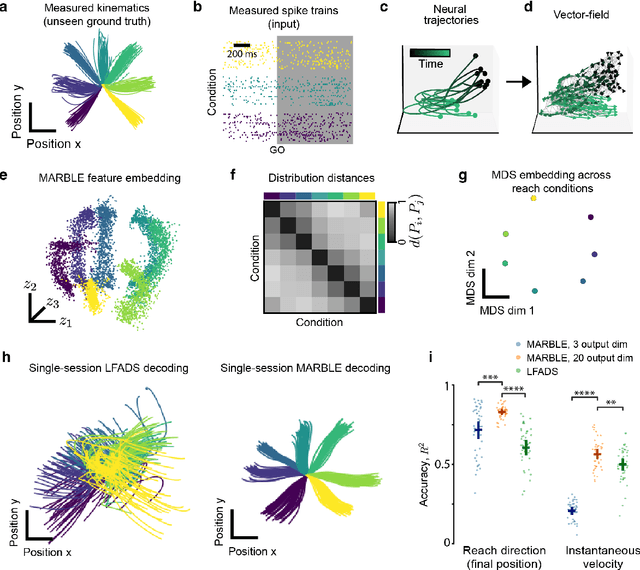
The dynamics of neuron populations during diverse tasks often evolve on low-dimensional manifolds. However, it remains challenging to discern the contributions of geometry and dynamics for encoding relevant behavioural variables. Here, we introduce an unsupervised geometric deep learning framework for representing non-linear dynamical systems based on statistical distributions of local phase portrait features. Our method provides robust geometry-aware or geometry-agnostic representations for the unbiased comparison of dynamics based on measured trajectories. We demonstrate that our statistical representation can generalise across neural network instances to discriminate computational mechanisms, obtain interpretable embeddings of neural dynamics in a primate reaching task with geometric correspondence to hand kinematics, and develop a decoding algorithm with state-of-the-art accuracy. Our results highlight the importance of using the intrinsic manifold structure over temporal information to develop better decoding algorithms and assimilate data across experiments.

Moment evolution equations and moment matching for stochastic image EPDiff

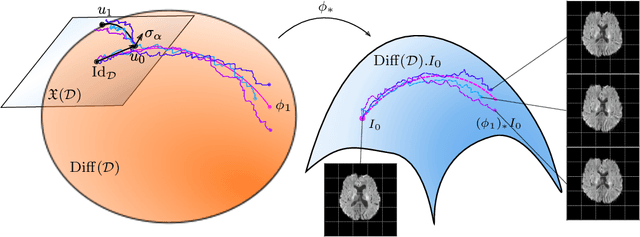
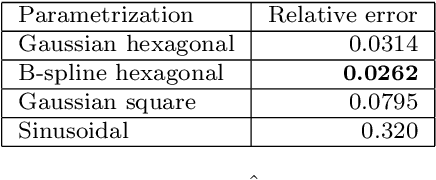
Models of stochastic image deformation allow study of time-continuous stochastic effects transforming images by deforming the image domain. Applications include longitudinal medical image analysis with both population trends and random subject specific variation. Focusing on a stochastic extension of the LDDMM models with evolutions governed by a stochastic EPDiff equation, we use moment approximations of the corresponding Ito diffusion to construct estimators for statistical inference in the full stochastic model. We show that this approach, when efficiently implemented with automatic differentiation tools, can successfully estimate parameters encoding the spatial correlation of the noise fields on the image

A Unifying and Canonical Description of Measure-Preserving Diffusions

A complete recipe of measure-preserving diffusions in Euclidean space was recently derived unifying several MCMC algorithms into a single framework. In this paper, we develop a geometric theory that improves and generalises this construction to any manifold. We thereby demonstrate that the completeness result is a direct consequence of the topology of the underlying manifold and the geometry induced by the target measure $P$; there is no need to introduce other structures such as a Riemannian metric, local coordinates, or a reference measure. Instead, our framework relies on the intrinsic geometry of $P$ and in particular its canonical derivative, the deRham rotationnel, which allows us to parametrise the Fokker--Planck currents of measure-preserving diffusions using potentials. The geometric formalism can easily incorporate constraints and symmetries, and deliver new important insights, for example, a new complete recipe of Langevin-like diffusions that are suited to the construction of samplers. We also analyse the reversibility and dissipative properties of the diffusions, the associated deterministic flow on the space of measures, and the geometry of Langevin processes. Our article connects ideas from various literature and frames the theory of measure-preserving diffusions in its appropriate mathematical context.

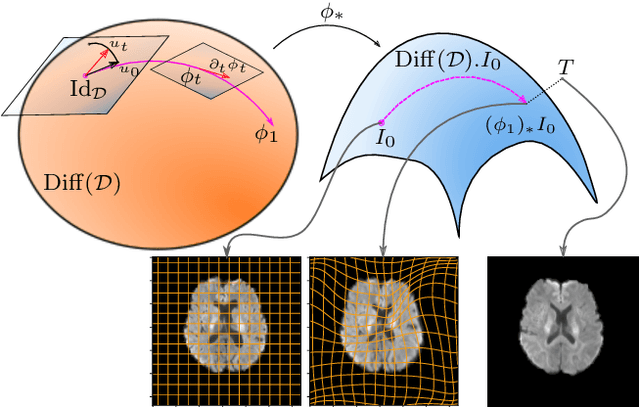
Diffusion bridges for stochastic Hamiltonian systems with applications to shape analysis

Stochastically evolving geometric systems are studied in geometric mechanics for modelling turbulence parts of multi-scale fluid flows and in shape analysis for stochastic evolutions of shapes of e.g. human organs. Recently introduced models involve stochastic differential equations that govern the dynamics of a diffusion process $X$. In applications $X$ is only partially observed at times $0$ and $T>0$. Conditional on these observations, interest lies in inferring parameters in the dynamics of the diffusion and reconstructing the path $(X_t,\, t\in [0,T])$. The latter problem is known as bridge simulation. We develop a general scheme for bridge sampling in the case of finite dimensional systems of shape landmarks and singular solutions in fluid dynamics. This scheme allows for subsequent statistical inference of properties of the fluid flow or the evolution of observed shapes. It covers stochastic landmark models for which no suitable simulation method has been proposed in the literature, that removes restrictions of earlier approaches, improves the handling of the nonlinearity of the configuration space leading to more effective sampling schemes and allows to generalise the common inexact matching scheme to the stochastic setting.

Semi-supervised classification on graphs using explicit diffusion dynamics

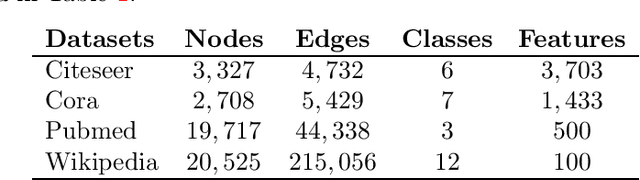
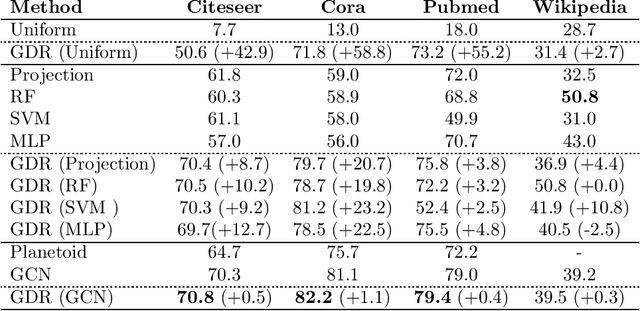
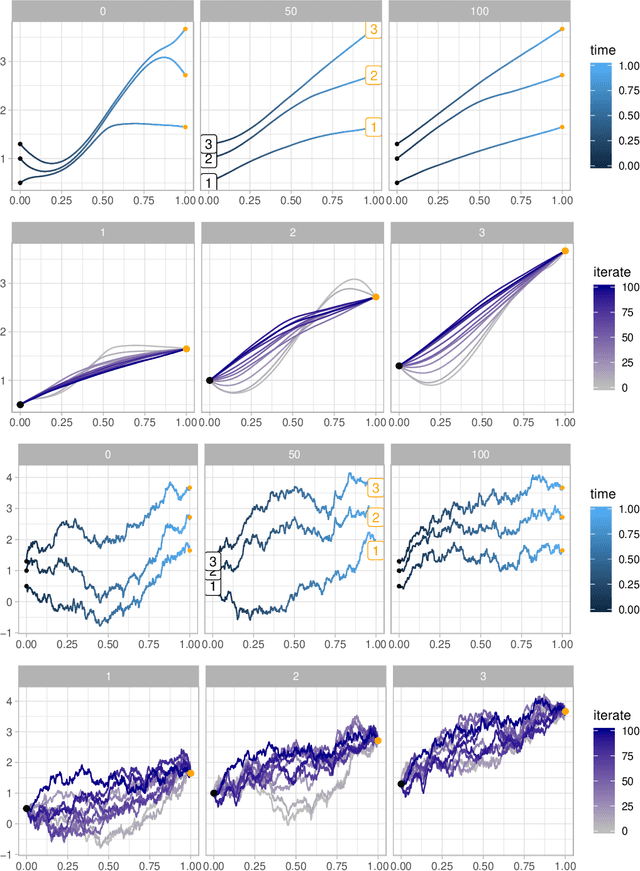
Classification tasks based on feature vectors can be significantly improved by including within deep learning a graph that summarises pairwise relationships between the samples. Intuitively, the graph acts as a conduit to channel and bias the inference of class labels. Here, we study classification methods that consider the graph as the originator of an explicit graph diffusion. We show that appending graph diffusion to feature-based learning as an \textit{a posteriori} refinement achieves state-of-the-art classification accuracy. This method, which we call Graph Diffusion Reclassification (GDR), uses overshooting events of a diffusive graph dynamics to reclassify individual nodes. The method uses intrinsic measures of node influence, which are distinct for each node, and allows the evaluation of the relationship and importance of features and graph for classification. We also present diff-GCN, a simple extension of Graph Convolutional Neural Network (GCN) architectures that leverages explicit diffusion dynamics, and allows the natural use of directed graphs. To showcase our methods, we use benchmark datasets of documents with associated citation data.

Selective metamorphosis for growth modelling with applications to landmarks

We present a framework for shape matching in computational anatomy allowing users control of the degree to which the matching is diffeomorphic. This control is given as a function defined over the image and parameterises the template deformation. By modelling localised template deformation we have a mathematical description of growth only in specified parts of an image. The location can either be specified from prior knowledge of the growth location or learned from data. For simplicity, we consider landmark matching and infer the distribution of a finite dimensional parameterisation of the control via Markov chain Monte Carlo. Preliminary numerical results are shown and future paths of investigation are laid out. Well-posedness of this new problem is studied together with an analysis of the associated geodesic equations.

Stochastic Image Deformation in Frequency Domain and Parameter Estimation using Moment Evolutions

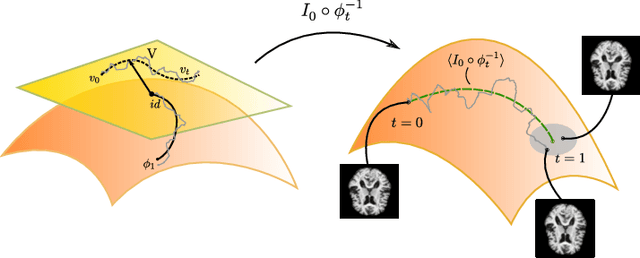
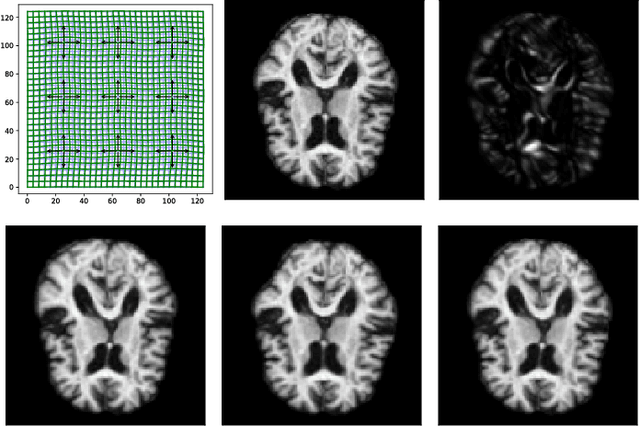
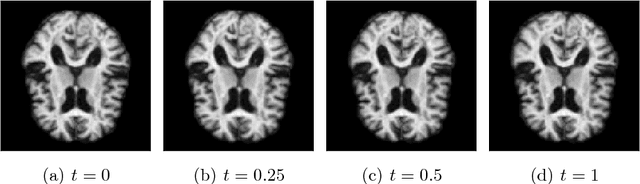
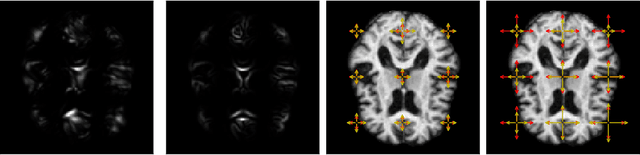
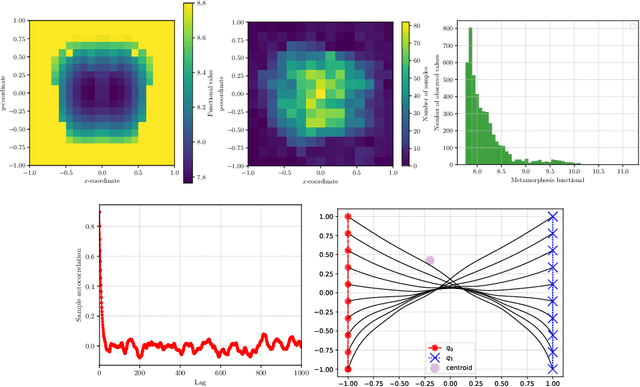
Modelling deformation of anatomical objects observed in medical images can help describe disease progression patterns and variations in anatomy across populations. We apply a stochastic generalisation of the Large Deformation Diffeomorphic Metric Mapping (LDDMM) framework to model differences in the evolution of anatomical objects detected in populations of image data. The computational challenges that are prevalent even in the deterministic LDDMM setting are handled by extending the FLASH LDDMM representation to the stochastic setting keeping a finite discretisation of the infinite dimensional space of image deformations. In this computationally efficient setting, we perform estimation to infer parameters for noise correlations and local variability in datasets of images. Fundamental for the optimisation procedure is using the finite dimensional Fourier representation to derive approximations of the evolution of moments for the stochastic warps. Particularly, the first moment allows us to infer deformation mean trajectories. The second moment encodes variation around the mean, and thus provides information on the noise correlation. We show on simulated datasets of 2D MR brain images that the estimation algorithm can successfully recover parameters of the stochastic model.

String Methods for Stochastic Image and Shape Matching

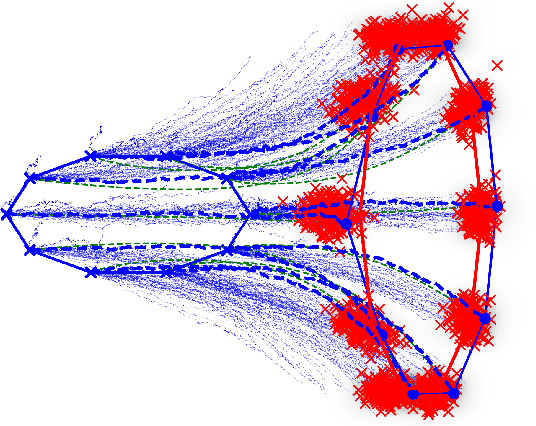
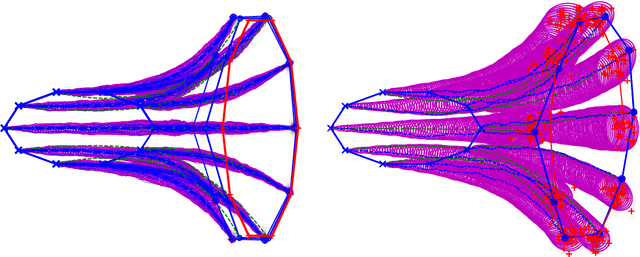
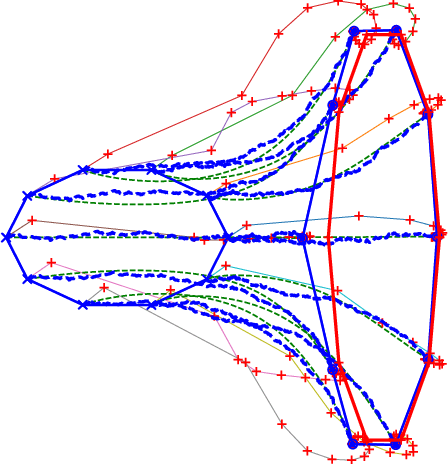
Matching of images and analysis of shape differences is traditionally pursued by energy minimization of paths of deformations acting to match the shape objects. In the Large Deformation Diffeomorphic Metric Mapping (LDDMM) framework, iterative gradient descents on the matching functional lead to matching algorithms informally known as Beg algorithms. When stochasticity is introduced to model stochastic variability of shapes and to provide more realistic models of observed shape data, the corresponding matching problem can be solved with a stochastic Beg algorithm, similar to the finite temperature string method used in rare event sampling. In this paper, we apply a stochastic model compatible with the geometry of the LDDMM framework to obtain a stochastic model of images and we derive the stochastic version of the Beg algorithm which we compare with the string method and an expectation-maximization optimization of posterior likelihoods. The algorithm and its use for statistical inference is tested on stochastic LDDMM landmarks and images.

A Geometric Framework for Stochastic Shape Analysis

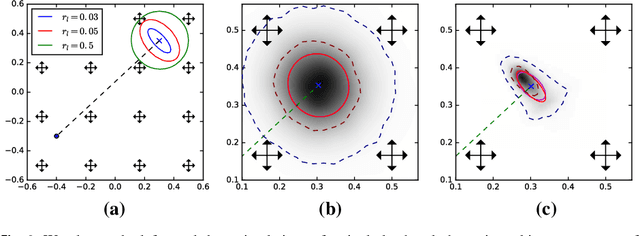
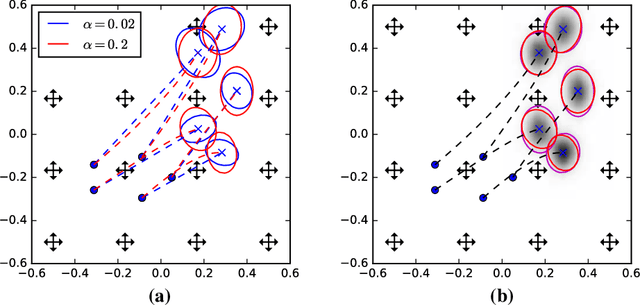
We introduce a stochastic model of diffeomorphisms, whose action on a variety of data types descends to stochastic evolution of shapes, images and landmarks. The stochasticity is introduced in the vector field which transports the data in the Large Deformation Diffeomorphic Metric Mapping (LDDMM) framework for shape analysis and image registration. The stochasticity thereby models errors or uncertainties of the flow in following the prescribed deformation velocity. The approach is illustrated in the example of finite dimensional landmark manifolds, whose stochastic evolution is studied both via the Fokker-Planck equation and by numerical simulations. We derive two approaches for inferring parameters of the stochastic model from landmark configurations observed at discrete time points. The first of the two approaches matches moments of the Fokker-Planck equation to sample moments of the data, while the second approach employs an Expectation-Maximisation based algorithm using a Monte Carlo bridge sampling scheme to optimise the data likelihood. We derive and numerically test the ability of the two approaches to infer the spatial correlation length of the underlying noise.

Stochastic metamorphosis with template uncertainties

In this paper, we investigate two stochastic perturbations of the metamorphosis equations of image analysis, in the geometrical context of the Euler-Poincar\'e theory. In the metamorphosis of images, the Lie group of diffeomorphisms deforms a template image that is undergoing its own internal dynamics as it deforms. This type of deformation allows more freedom for image matching and has analogies with complex fluids when the template properties are regarded as order parameters (coset spaces of broken symmetries). The first stochastic perturbation we consider corresponds to uncertainty due to random errors in the reconstruction of the deformation map from its vector field. We also consider a second stochastic perturbation, which compounds the uncertainty in of the deformation map with the uncertainty in the reconstruction of the template position from its velocity field. We apply this general geometric theory to several classical examples, including landmarks, images, and closed curves, and we discuss its use for functional data analysis.