Geometry matters: Exploring language examples at the decision boundary

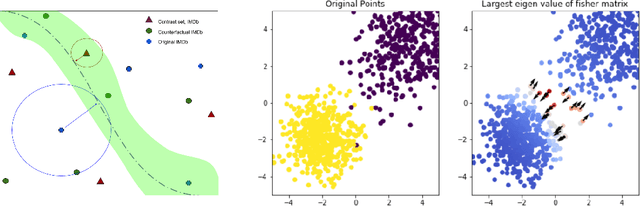
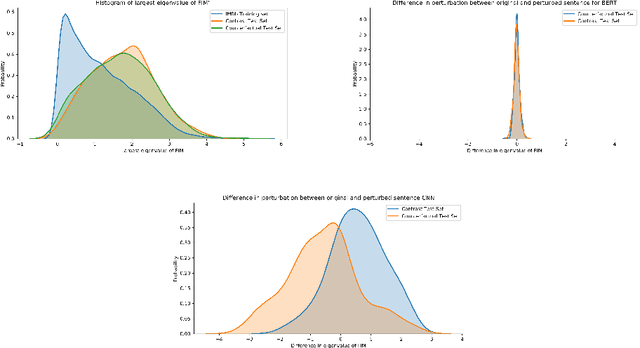
A growing body of recent evidence has highlighted the limitations of natural language processing (NLP) datasets and classifiers. These include the presence of annotation artifacts in datasets, classifiers relying on shallow features like a single word (e.g., if a movie review has the word "romantic", the review tends to be positive), or unnecessary words (e.g., learning a proper noun to classify a movie as positive or negative). The presence of such artifacts has subsequently led to the development of challenging datasets to force the model to generalize better. While a variety of heuristic strategies, such as counterfactual examples and contrast sets, have been proposed, the theoretical justification about what makes these examples difficult is often lacking or unclear. In this paper, using tools from information geometry, we propose a theoretical way to quantify the difficulty of an example in NLP. Using our approach, we explore difficult examples for two popular NLP architectures. We discover that both BERT and CNN are susceptible to single word substitutions in high difficulty examples. Consequently, examples with low difficulty scores tend to be robust to multiple word substitutions. Our analysis shows that perturbations like contrast sets and counterfactual examples are not necessarily difficult for the model, and they may not be accomplishing the intended goal. Our approach is simple, architecture agnostic, and easily extendable to other datasets. All the code used will be made publicly available, including a tool to explore the difficult examples for other datasets.

Stochastic Image Deformation in Frequency Domain and Parameter Estimation using Moment Evolutions

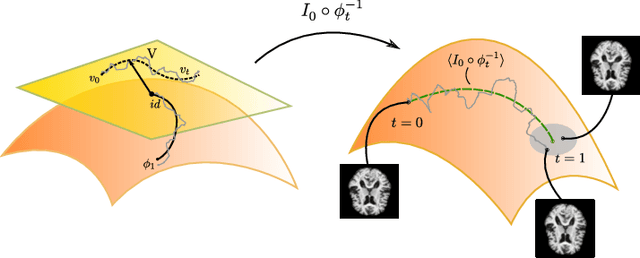
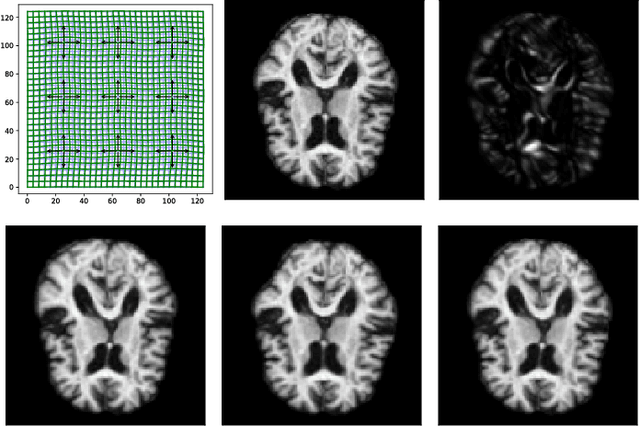
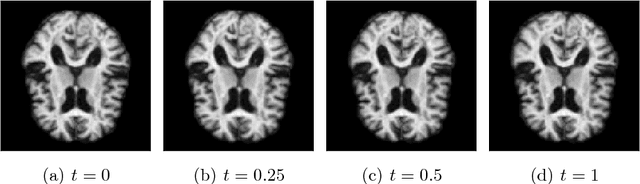
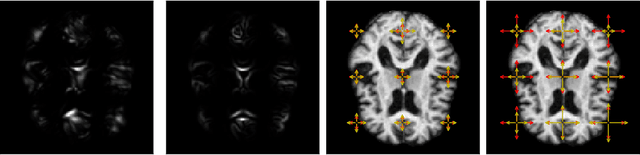
Modelling deformation of anatomical objects observed in medical images can help describe disease progression patterns and variations in anatomy across populations. We apply a stochastic generalisation of the Large Deformation Diffeomorphic Metric Mapping (LDDMM) framework to model differences in the evolution of anatomical objects detected in populations of image data. The computational challenges that are prevalent even in the deterministic LDDMM setting are handled by extending the FLASH LDDMM representation to the stochastic setting keeping a finite discretisation of the infinite dimensional space of image deformations. In this computationally efficient setting, we perform estimation to infer parameters for noise correlations and local variability in datasets of images. Fundamental for the optimisation procedure is using the finite dimensional Fourier representation to derive approximations of the evolution of moments for the stochastic warps. Particularly, the first moment allows us to infer deformation mean trajectories. The second moment encodes variation around the mean, and thus provides information on the noise correlation. We show on simulated datasets of 2D MR brain images that the estimation algorithm can successfully recover parameters of the stochastic model.

Deep Diffeomorphic Normalizing Flows

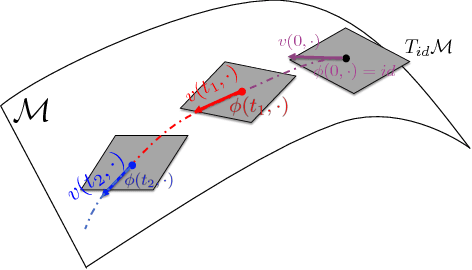
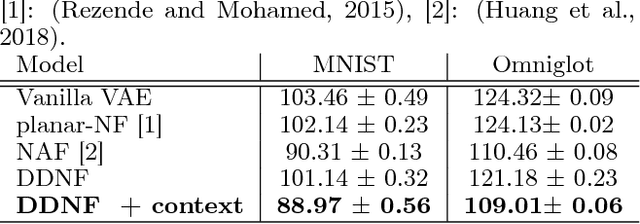
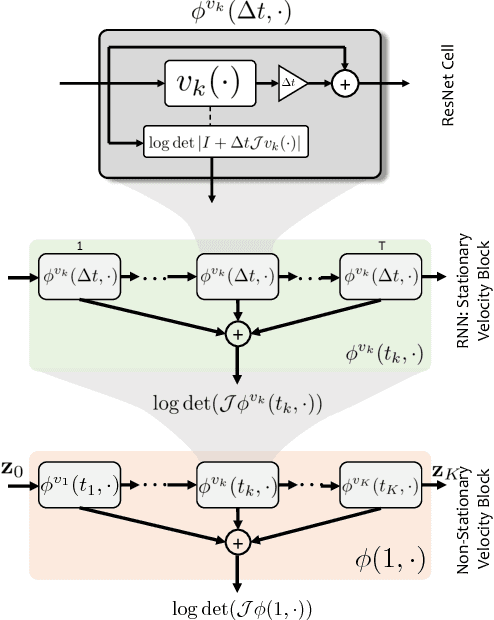
The Normalizing Flow (NF) models a general probability density by estimating an invertible transformation applied on samples drawn from a known distribution. We introduce a new type of NF, called Deep Diffeomorphic Normalizing Flow (DDNF). A diffeomorphic flow is an invertible function where both the function and its inverse are smooth. We construct the flow using an ordinary differential equation (ODE) governed by a time-varying smooth vector field. We use a neural network to parametrize the smooth vector field and a recursive neural network (RNN) for approximating the solution of the ODE. Each cell in the RNN is a residual network implementing one Euler integration step. The architecture of our flow enables efficient likelihood evaluation, straightforward flow inversion, and results in highly flexible density estimation. An end-to-end trained DDNF achieves competitive results with state-of-the-art methods on a suite of density estimation and variational inference tasks. Finally, our method brings concepts from Riemannian geometry that, we believe, can open a new research direction for neural density estimation.

Latent Space Non-Linear Statistics

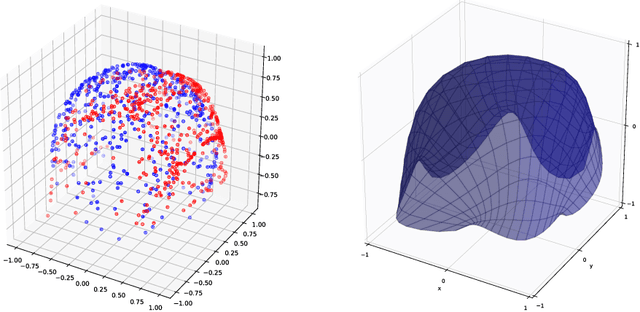
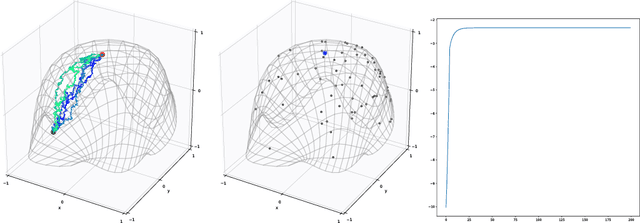
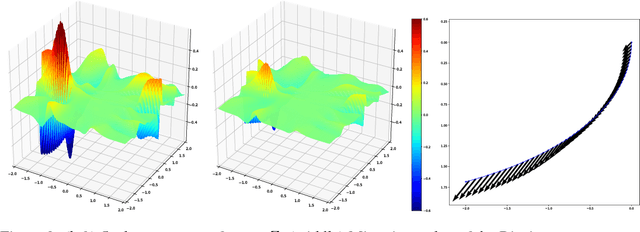
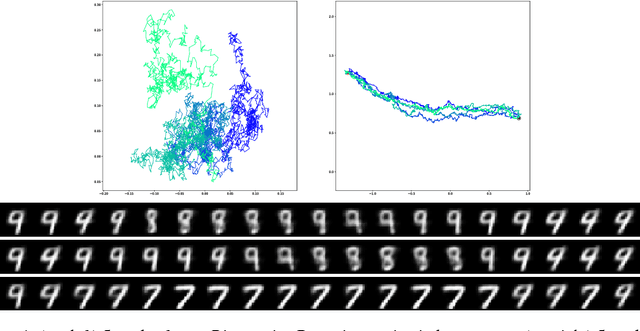
Given data, deep generative models, such as variational autoencoders (VAE) and generative adversarial networks (GAN), train a lower dimensional latent representation of the data space. The linear Euclidean geometry of data space pulls back to a nonlinear Riemannian geometry on the latent space. The latent space thus provides a low-dimensional nonlinear representation of data and classical linear statistical techniques are no longer applicable. In this paper we show how statistics of data in their latent space representation can be performed using techniques from the field of nonlinear manifold statistics. Nonlinear manifold statistics provide generalizations of Euclidean statistical notions including means, principal component analysis, and maximum likelihood fits of parametric probability distributions. We develop new techniques for maximum likelihood inference in latent space, and adress the computational complexity of using geometric algorithms with high-dimensional data by training a separate neural network to approximate the Riemannian metric and cometric tensor capturing the shape of the learned data manifold.