Stochastic Image Deformation in Frequency Domain and Parameter Estimation using Moment Evolutions
Paper and Code
Dec 13, 2018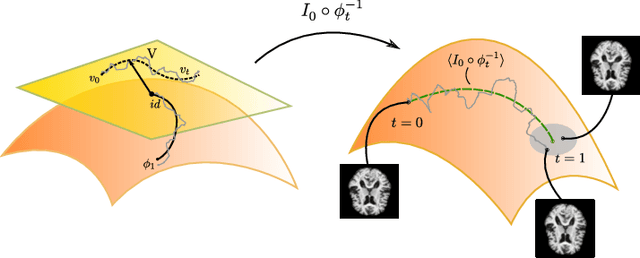
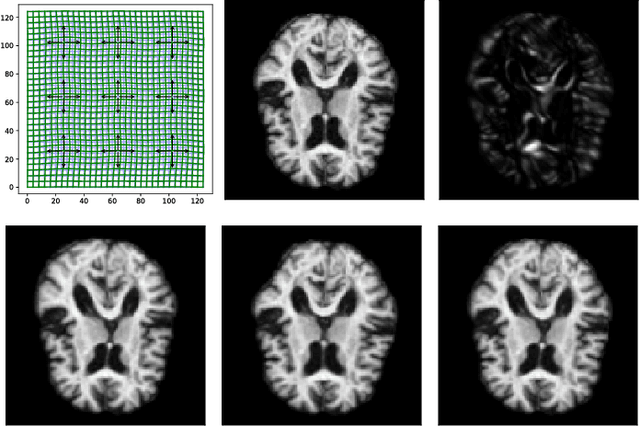
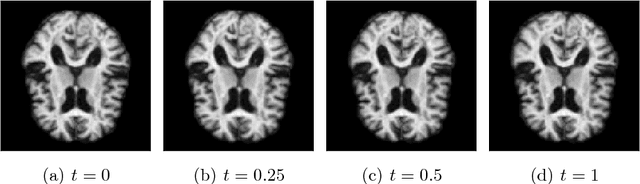
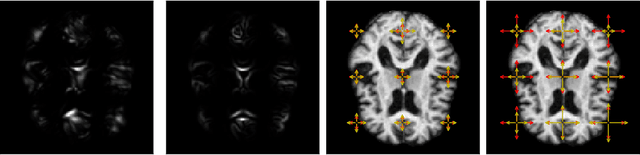
Modelling deformation of anatomical objects observed in medical images can help describe disease progression patterns and variations in anatomy across populations. We apply a stochastic generalisation of the Large Deformation Diffeomorphic Metric Mapping (LDDMM) framework to model differences in the evolution of anatomical objects detected in populations of image data. The computational challenges that are prevalent even in the deterministic LDDMM setting are handled by extending the FLASH LDDMM representation to the stochastic setting keeping a finite discretisation of the infinite dimensional space of image deformations. In this computationally efficient setting, we perform estimation to infer parameters for noise correlations and local variability in datasets of images. Fundamental for the optimisation procedure is using the finite dimensional Fourier representation to derive approximations of the evolution of moments for the stochastic warps. Particularly, the first moment allows us to infer deformation mean trajectories. The second moment encodes variation around the mean, and thus provides information on the noise correlation. We show on simulated datasets of 2D MR brain images that the estimation algorithm can successfully recover parameters of the stochastic model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge