Stochastic Image Deformation in Frequency Domain and Parameter Estimation using Moment Evolutions

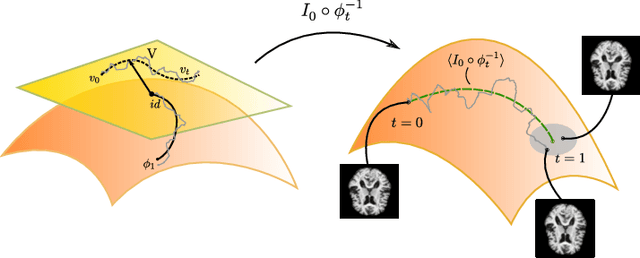
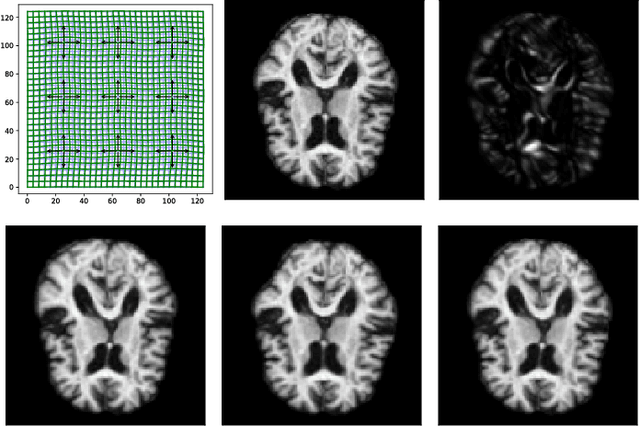
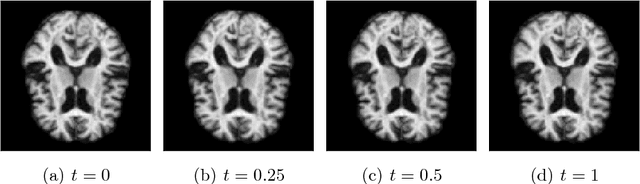
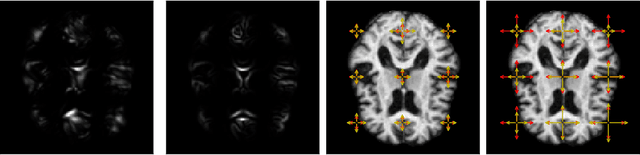
Modelling deformation of anatomical objects observed in medical images can help describe disease progression patterns and variations in anatomy across populations. We apply a stochastic generalisation of the Large Deformation Diffeomorphic Metric Mapping (LDDMM) framework to model differences in the evolution of anatomical objects detected in populations of image data. The computational challenges that are prevalent even in the deterministic LDDMM setting are handled by extending the FLASH LDDMM representation to the stochastic setting keeping a finite discretisation of the infinite dimensional space of image deformations. In this computationally efficient setting, we perform estimation to infer parameters for noise correlations and local variability in datasets of images. Fundamental for the optimisation procedure is using the finite dimensional Fourier representation to derive approximations of the evolution of moments for the stochastic warps. Particularly, the first moment allows us to infer deformation mean trajectories. The second moment encodes variation around the mean, and thus provides information on the noise correlation. We show on simulated datasets of 2D MR brain images that the estimation algorithm can successfully recover parameters of the stochastic model.

A Statistical Model for Simultaneous Template Estimation, Bias Correction, and Registration of 3D Brain Images

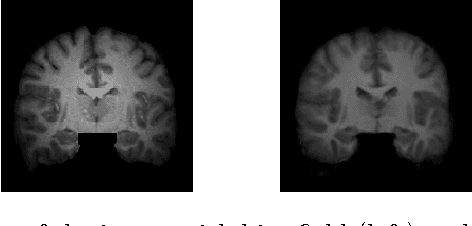
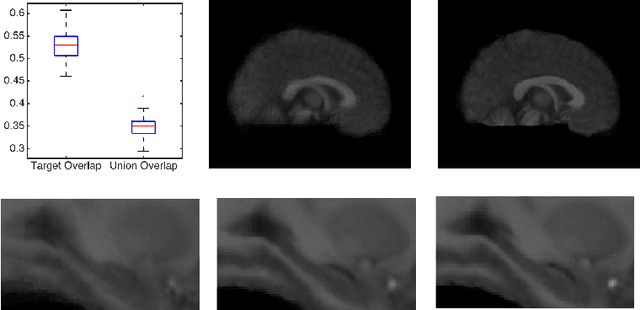
Template estimation plays a crucial role in computational anatomy since it provides reference frames for performing statistical analysis of the underlying anatomical population variability. While building models for template estimation, variability in sites and image acquisition protocols need to be accounted for. To account for such variability, we propose a generative template estimation model that makes simultaneous inference of both bias fields in individual images, deformations for image registration, and variance hyperparameters. In contrast, existing maximum a posterori based methods need to rely on either bias-invariant similarity measures or robust image normalization. Results on synthetic and real brain MRI images demonstrate the capability of the model to capture heterogeneity in intensities and provide a reliable template estimation from registration.

Most Likely Separation of Intensity and Warping Effects in Image Registration

This paper introduces a class of mixed-effects models for joint modeling of spatially correlated intensity variation and warping variation in 2D images. Spatially correlated intensity variation and warp variation are modeled as random effects, resulting in a nonlinear mixed-effects model that enables simultaneous estimation of template and model parameters by optimization of the likelihood function. We propose an algorithm for fitting the model which alternates estimation of variance parameters and image registration. This approach avoids the potential estimation bias in the template estimate that arises when treating registration as a preprocessing step. We apply the model to datasets of facial images and 2D brain magnetic resonance images to illustrate the simultaneous estimation and prediction of intensity and warp effects.