Parameter Inference via Differentiable Diffusion Bridge Importance Sampling

We introduce a methodology for performing parameter inference in high-dimensional, non-linear diffusion processes. We illustrate its applicability for obtaining insights into the evolution of and relationships between species, including ancestral state reconstruction. Estimation is performed by utilising score matching to approximate diffusion bridges, which are subsequently used in an importance sampler to estimate log-likelihoods. The entire setup is differentiable, allowing gradient ascent on approximated log-likelihoods. This allows both parameter inference and diffusion mean estimation. This novel, numerically stable, score matching-based parameter inference framework is presented and demonstrated on biological two- and three-dimensional morphometry data.

Parallel transport on matrix manifolds and Exponential Action

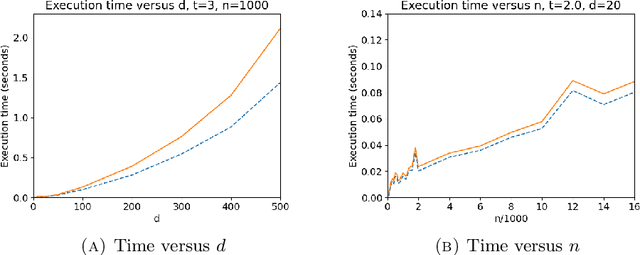
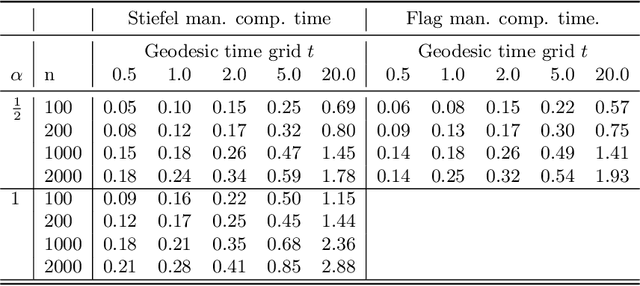
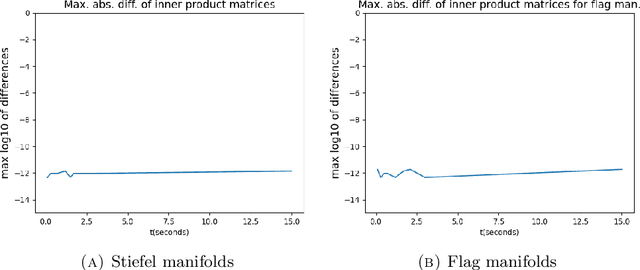
We express parallel transport for several common matrix Lie groups with a family of pseudo-Riemannian metrics in terms of matrix exponential and exponential actions. The expression for parallel transport is preserved by taking the quotient under certain scenarios. In particular, for a Stiefel manifold of orthogonal matrices of size $n\times d$, we give an expression for parallel transport along a geodesic from time zero to $t$, that could be computed with time complexity of $O(nd^2)$ for small $t$, and of $O(td^3)$ for large t, contributing a step in a long-standing open problem in matrix manifolds. A similar result holds for flag manifolds with the canonical metric. We also show the parallel transport formulas for the generalized linear group, and the special orthogonal group under these metrics.

Score matching for bridges without time-reversals

We propose a new algorithm for learning a bridged diffusion process using score-matching methods. Our method relies on reversing the dynamics of the forward process and using this to learn a score function, which, via Doob's $h$-transform, gives us a bridged diffusion process; that is, a process conditioned on an endpoint. In contrast to prior methods, ours learns the score term $\nabla_x \log p(t, x; T, y)$, for given $t, Y$ directly, completely avoiding the need for first learning a time reversal. We compare the performance of our algorithm with existing methods and see that it outperforms using the (learned) time-reversals to learn the score term. The code can be found at https://github.com/libbylbaker/forward_bridge.

Second-order differential operators, stochastic differential equations and Brownian motions on embedded manifolds

We specify the conditions when a manifold M embedded in an inner product space E is an invariant manifold of a stochastic differential equation (SDE) on E, linking it with the notion of second-order differential operators on M. When M is given a Riemannian metric, we derive a simple formula for the Laplace-Beltrami operator in terms of the gradient and Hessian on E and construct the Riemannian Brownian motions on M as solutions of conservative Stratonovich and Ito SDEs on E. We derive explicitly the SDE for Brownian motions on several important manifolds in applications, including left-invariant matrix Lie groups using embedded coordinates. Numerically, we propose three simulation schemes to solve SDEs on manifolds. In addition to the stochastic projection method, to simulate Riemannian Brownian motions, we construct a second-order tangent retraction of the Levi-Civita connection using a given E-tubular retraction. We also propose the retractive Euler-Maruyama method to solve a SDE, taking into account the second-order term of a tangent retraction. We provide software to implement the methods in the paper, including Brownian motions of the manifolds discussed. We verify numerically that on several compact Riemannian manifolds, the long-term limit of Brownian simulation converges to the uniform distributions, suggesting a method to sample Riemannian uniform distributions

Simulating infinite-dimensional nonlinear diffusion bridges

The diffusion bridge is a type of diffusion process that conditions on hitting a specific state within a finite time period. It has broad applications in fields such as Bayesian inference, financial mathematics, control theory, and shape analysis. However, simulating the diffusion bridge for natural data can be challenging due to both the intractability of the drift term and continuous representations of the data. Although several methods are available to simulate finite-dimensional diffusion bridges, infinite-dimensional cases remain unresolved. In the paper, we present a solution to this problem by merging score-matching techniques with operator learning, enabling a direct approach to score-matching for the infinite-dimensional bridge. We construct the score to be discretization invariant, which is natural given the underlying spatially continuous process. We conduct a series of experiments, ranging from synthetic examples with closed-form solutions to the stochastic nonlinear evolution of real-world biological shape data, and our method demonstrates high efficacy, particularly due to its ability to adapt to any resolution without extra training.

Score matching for sub-Riemannian bridge sampling

Simulation of conditioned diffusion processes is an essential tool in inference for stochastic processes, data imputation, generative modelling, and geometric statistics. Whilst simulating diffusion bridge processes is already difficult on Euclidean spaces, when considering diffusion processes on Riemannian manifolds the geometry brings in further complications. In even higher generality, advancing from Riemannian to sub-Riemannian geometries introduces hypoellipticity, and the possibility of finding appropriate explicit approximations for the score of the diffusion process is removed. We handle these challenges and construct a method for bridge simulation on sub-Riemannian manifolds by demonstrating how recent progress in machine learning can be modified to allow for training of score approximators on sub-Riemannian manifolds. Since gradients dependent on the horizontal distribution, we generalise the usual notion of denoising loss to work with non-holonomic frames using a stochastic Taylor expansion, and we demonstrate the resulting scheme both explicitly on the Heisenberg group and more generally using adapted coordinates. We perform numerical experiments exemplifying samples from the bridge process on the Heisenberg group and the concentration of this process for small time.

Conditioning non-linear and infinite-dimensional diffusion processes

Generative diffusion models and many stochastic models in science and engineering naturally live in infinite dimensions before discretisation. To incorporate observed data for statistical and learning tasks, one needs to condition on observations. While recent work has treated conditioning linear processes in infinite dimensions, conditioning non-linear processes in infinite dimensions has not been explored. This paper conditions function valued stochastic processes without prior discretisation. To do so, we use an infinite-dimensional version of Girsanov's theorem to condition a function-valued stochastic process, leading to a stochastic differential equation (SDE) for the conditioned process involving the score. We apply this technique to do time series analysis for shapes of organisms in evolutionary biology, where we discretise via the Fourier basis and then learn the coefficients of the score function with score matching methods.

Principal subbundles for dimension reduction

In this paper we demonstrate how sub-Riemannian geometry can be used for manifold learning and surface reconstruction by combining local linear approximations of a point cloud to obtain lower dimensional bundles. Local approximations obtained by local PCAs are collected into a rank $k$ tangent subbundle on $\mathbb{R}^d$, $k<d$, which we call a principal subbundle. This determines a sub-Riemannian metric on $\mathbb{R}^d$. We show that sub-Riemannian geodesics with respect to this metric can successfully be applied to a number of important problems, such as: explicit construction of an approximating submanifold $M$, construction of a representation of the point-cloud in $\mathbb{R}^k$, and computation of distances between observations, taking the learned geometry into account. The reconstruction is guaranteed to equal the true submanifold in the limit case where tangent spaces are estimated exactly. Via simulations, we show that the framework is robust when applied to noisy data. Furthermore, the framework generalizes to observations on an a priori known Riemannian manifold.

Sliding at first order: Higher-order momentum distributions for discontinuous image registration

In this paper, we propose a new approach to deformable image registration that captures sliding motions. The large deformation diffeomorphic metric mapping (LDDMM) registration method faces challenges in representing sliding motion since it per construction generates smooth warps. To address this issue, we extend LDDMM by incorporating both zeroth- and first-order momenta with a non-differentiable kernel. This allows to represent both discontinuous deformation at switching boundaries and diffeomorphic deformation in homogeneous regions. We provide a mathematical analysis of the proposed deformation model from the viewpoint of discontinuous systems. To evaluate our approach, we conduct experiments on both artificial images and the publicly available DIR-Lab 4DCT dataset. Results show the effectiveness of our approach in capturing plausible sliding motion.

Deep Anatomical Federated Network (Dafne): an open client/server framework for the continuous collaborative improvement of deep-learning-based medical image segmentation

Semantic segmentation is a crucial step to extract quantitative information from medical (and, specifically, radiological) images to aid the diagnostic process, clinical follow-up. and to generate biomarkers for clinical research. In recent years, machine learning algorithms have become the primary tool for this task. However, its real-world performance is heavily reliant on the comprehensiveness of training data. Dafne is the first decentralized, collaborative solution that implements continuously evolving deep learning models exploiting the collective knowledge of the users of the system. In the Dafne workflow, the result of each automated segmentation is refined by the user through an integrated interface, so that the new information is used to continuously expand the training pool via federated incremental learning. The models deployed through Dafne are able to improve their performance over time and to generalize to data types not seen in the training sets, thus becoming a viable and practical solution for real-life medical segmentation tasks.