Parsimonious Gaussian mixture models with piecewise-constant eigenvalue profiles

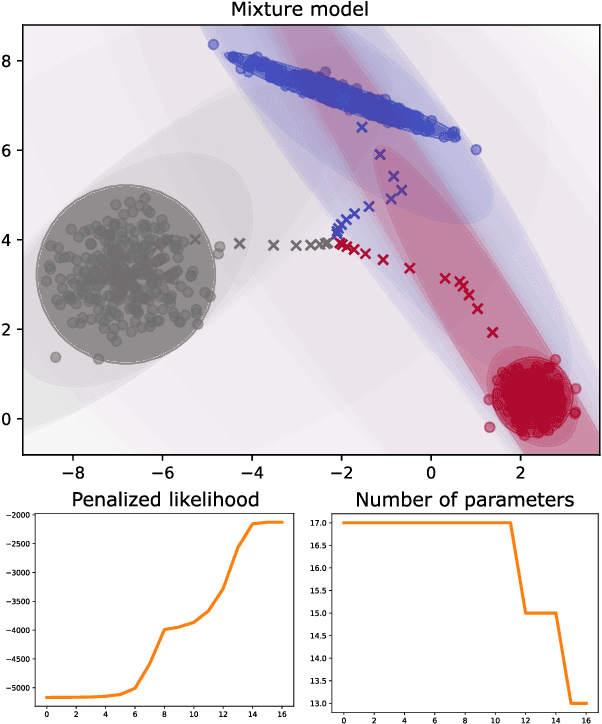
Gaussian mixture models (GMMs) are ubiquitous in statistical learning, particularly for unsupervised problems. While full GMMs suffer from the overparameterization of their covariance matrices in high-dimensional spaces, spherical GMMs (with isotropic covariance matrices) certainly lack flexibility to fit certain anisotropic distributions. Connecting these two extremes, we introduce a new family of parsimonious GMMs with piecewise-constant covariance eigenvalue profiles. These extend several low-rank models like the celebrated mixtures of probabilistic principal component analyzers (MPPCA), by enabling any possible sequence of eigenvalue multiplicities. If the latter are prespecified, then we can naturally derive an expectation-maximization (EM) algorithm to learn the mixture parameters. Otherwise, to address the notoriously-challenging issue of jointly learning the mixture parameters and hyperparameters, we propose a componentwise penalized EM algorithm, whose monotonicity is proven. We show the superior likelihood-parsimony tradeoffs achieved by our models on a variety of unsupervised experiments: density fitting, clustering and single-image denoising.

Nested subspace learning with flags

Many machine learning methods look for low-dimensional representations of the data. The underlying subspace can be estimated by first choosing a dimension $q$ and then optimizing a certain objective function over the space of $q$-dimensional subspaces (the Grassmannian). Trying different $q$ yields in general non-nested subspaces, which raises an important issue of consistency between the data representations. In this paper, we propose a simple trick to enforce nestedness in subspace learning methods. It consists in lifting Grassmannian optimization problems to flag manifolds (the space of nested subspaces of increasing dimension) via nested projectors. We apply the flag trick to several classical machine learning methods and show that it successfully addresses the nestedness issue.

Beyond Euclid: An Illustrated Guide to Modern Machine Learning with Geometric, Topological, and Algebraic Structures

The enduring legacy of Euclidean geometry underpins classical machine learning, which, for decades, has been primarily developed for data lying in Euclidean space. Yet, modern machine learning increasingly encounters richly structured data that is inherently nonEuclidean. This data can exhibit intricate geometric, topological and algebraic structure: from the geometry of the curvature of space-time, to topologically complex interactions between neurons in the brain, to the algebraic transformations describing symmetries of physical systems. Extracting knowledge from such non-Euclidean data necessitates a broader mathematical perspective. Echoing the 19th-century revolutions that gave rise to non-Euclidean geometry, an emerging line of research is redefining modern machine learning with non-Euclidean structures. Its goal: generalizing classical methods to unconventional data types with geometry, topology, and algebra. In this review, we provide an accessible gateway to this fast-growing field and propose a graphical taxonomy that integrates recent advances into an intuitive unified framework. We subsequently extract insights into current challenges and highlight exciting opportunities for future development in this field.

Principal subbundles for dimension reduction

In this paper we demonstrate how sub-Riemannian geometry can be used for manifold learning and surface reconstruction by combining local linear approximations of a point cloud to obtain lower dimensional bundles. Local approximations obtained by local PCAs are collected into a rank $k$ tangent subbundle on $\mathbb{R}^d$, $k<d$, which we call a principal subbundle. This determines a sub-Riemannian metric on $\mathbb{R}^d$. We show that sub-Riemannian geodesics with respect to this metric can successfully be applied to a number of important problems, such as: explicit construction of an approximating submanifold $M$, construction of a representation of the point-cloud in $\mathbb{R}^k$, and computation of distances between observations, taking the learned geometry into account. The reconstruction is guaranteed to equal the true submanifold in the limit case where tangent spaces are estimated exactly. Via simulations, we show that the framework is robust when applied to noisy data. Furthermore, the framework generalizes to observations on an a priori known Riemannian manifold.

Geodesic squared exponential kernel for non-rigid shape registration

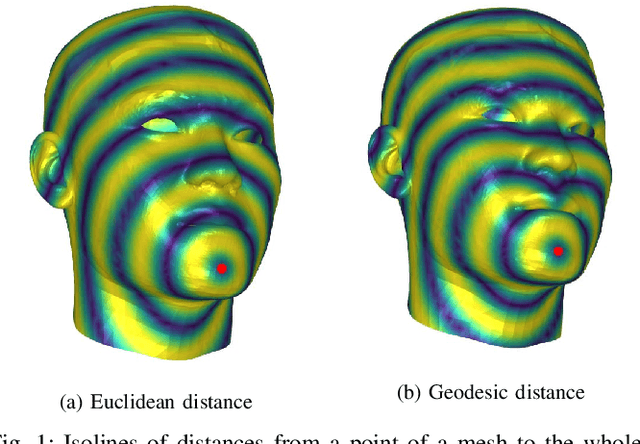
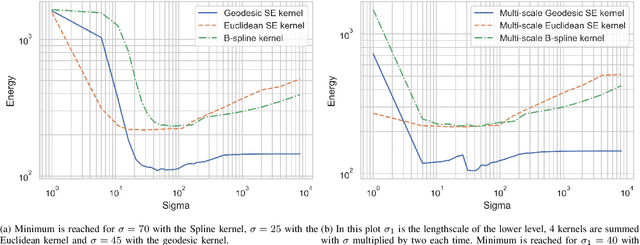
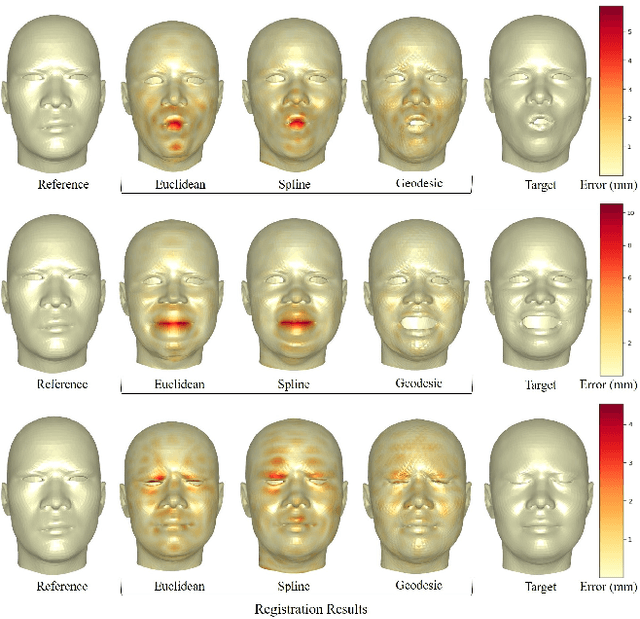
This work addresses the problem of non-rigid registration of 3D scans, which is at the core of shape modeling techniques. Firstly, we propose a new kernel based on geodesic distances for the Gaussian Process Morphable Models (GPMMs) framework. The use of geodesic distances into the kernel makes it more adapted to the topological and geometric characteristics of the surface and leads to more realistic deformations around holes and curved areas. Since the kernel possesses hyperparameters we have optimized them for the task of face registration on the FaceWarehouse dataset. We show that the Geodesic squared exponential kernel performs significantly better than state of the art kernels for the task of face registration on all the 20 expressions of the FaceWarehouse dataset. Secondly, we propose a modification of the loss function used in the non-rigid ICP registration algorithm, that allows to weight the correspondences according to the confidence given to them. As a use case, we show that we can make the registration more robust to outliers in the 3D scans, such as non-skin parts.

Cardiac Motion Modeling with Parallel Transport and Shape Splines

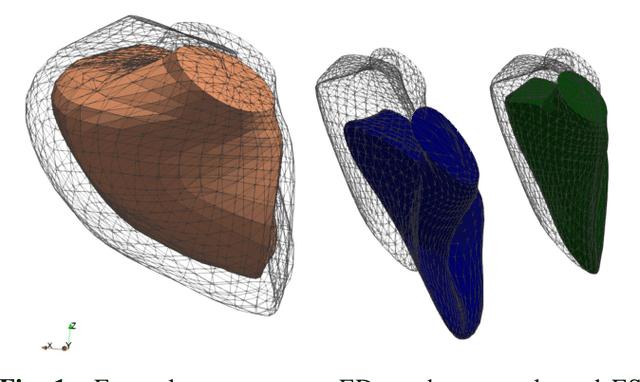
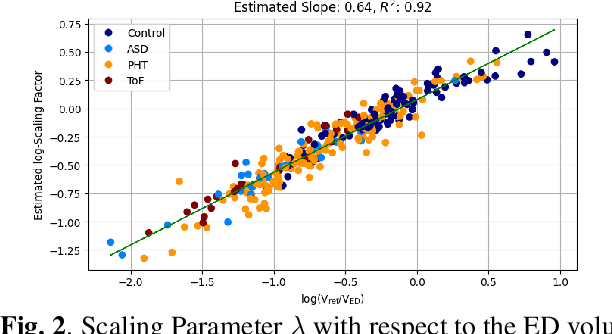
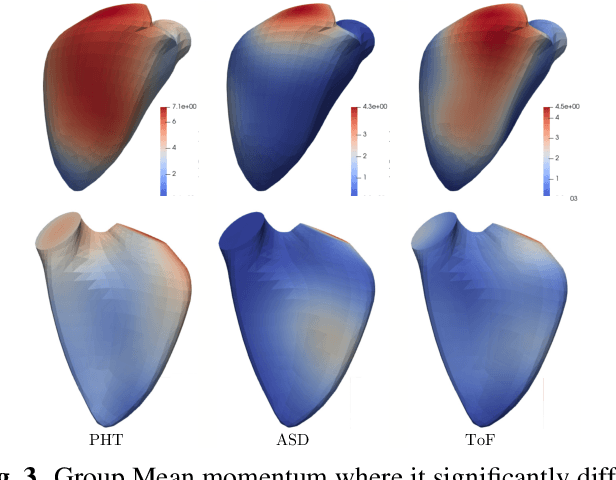
In cases of pressure or volume overload, probing cardiac function may be difficult because of the interactions between shape and deformations.In this work, we use the LDDMM framework and parallel transport to estimate and reorient deformations of the right ventricle. We then propose a normalization procedure for the amplitude of the deformation, and a second-order spline model to represent the full cardiac contraction. The method is applied to 3D meshes of the right ventricle extracted from echocardiographic sequences of 314 patients divided into three disease categories and a control group. We find significant differences between pathologies in the model parameters, revealing insights into the dynamics of each disease.

Geomstats: A Python Package for Riemannian Geometry in Machine Learning

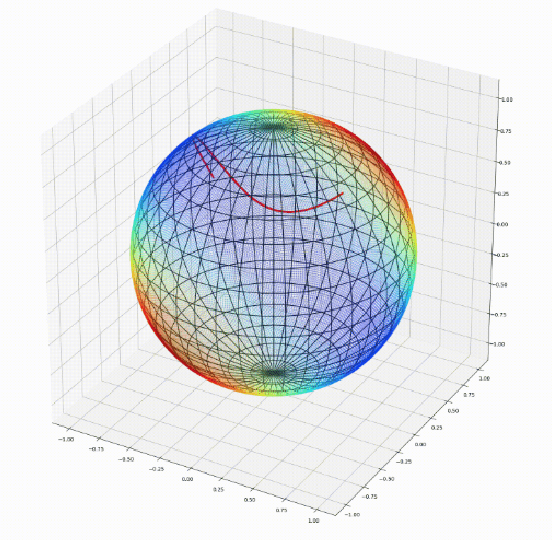
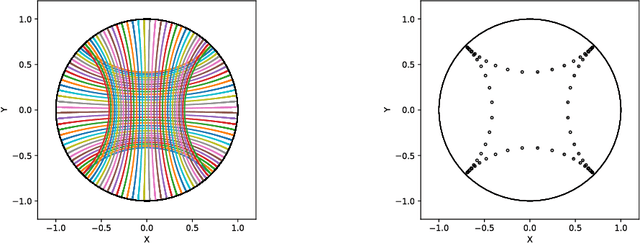
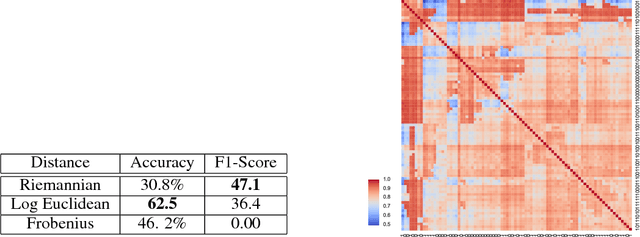
We introduce Geomstats, an open-source Python toolbox for computations and statistics on nonlinear manifolds, such as hyperbolic spaces, spaces of symmetric positive definite matrices, Lie groups of transformations, and many more. We provide object-oriented and extensively unit-tested implementations. Among others, manifolds come equipped with families of Riemannian metrics, with associated exponential and logarithmic maps, geodesics and parallel transport. Statistics and learning algorithms provide methods for estimation, clustering and dimension reduction on manifolds. All associated operations are vectorized for batch computation and provide support for different execution backends, namely NumPy, PyTorch and TensorFlow, enabling GPU acceleration. This paper presents the package, compares it with related libraries and provides relevant code examples. We show that Geomstats provides reliable building blocks to foster research in differential geometry and statistics, and to democratize the use of Riemannian geometry in machine learning applications. The source code is freely available under the MIT license at \url{geomstats.ai}.

A model of brain morphological changes related to aging and Alzheimer's disease from cross-sectional assessments

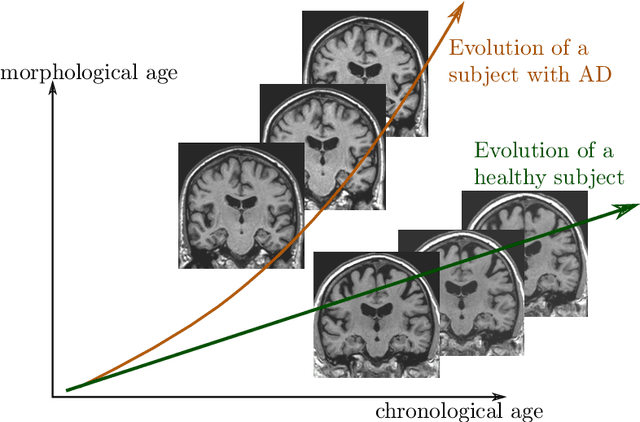
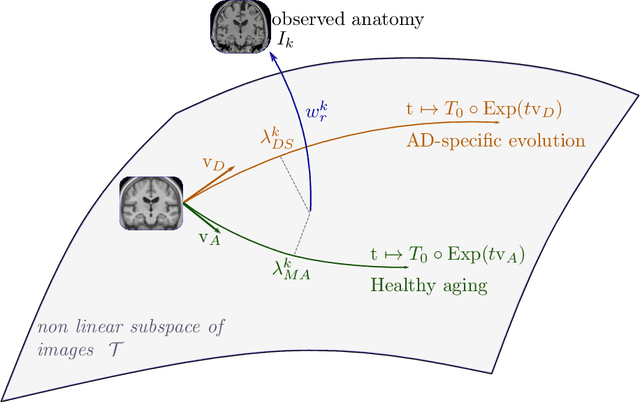
In this study we propose a deformation-based framework to jointly model the influence of aging and Alzheimer's disease (AD) on the brain morphological evolution. Our approach combines a spatio-temporal description of both processes into a generative model. A reference morphology is deformed along specific trajectories to match subject specific morphologies. It is used to define two imaging progression markers: 1) a morphological age and 2) a disease score. These markers can be computed locally in any brain region. The approach is evaluated on brain structural magnetic resonance images (MRI) from the ADNI database. The generative model is first estimated on a control population, then, for each subject, the markers are computed for each acquisition. The longitudinal evolution of these markers is then studied in relation with the clinical diagnosis of the subjects and used to generate possible morphological evolution. In the model, the morphological changes associated with normal aging are mainly found around the ventricles, while the Alzheimer's disease specific changes are more located in the temporal lobe and the hippocampal area. The statistical analysis of these markers highlights differences between clinical conditions even though the inter-subject variability is quiet high. In this context, the model can be used to generate plausible morphological trajectories associated with the disease. Our method gives two interpretable scalar imaging biomarkers assessing the effects of aging and disease on brain morphology at the individual and population level. These markers confirm an acceleration of apparent aging for Alzheimer's subjects and can help discriminate clinical conditions even in prodromal stages. More generally, the joint modeling of normal and pathological evolutions shows promising results to describe age-related brain diseases over long time scales.

Automatically Segmenting the Left Atrium from Cardiac Images Using Successive 3D U-Nets and a Contour Loss

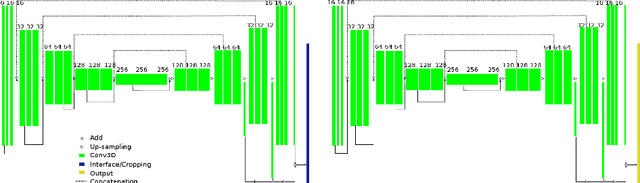
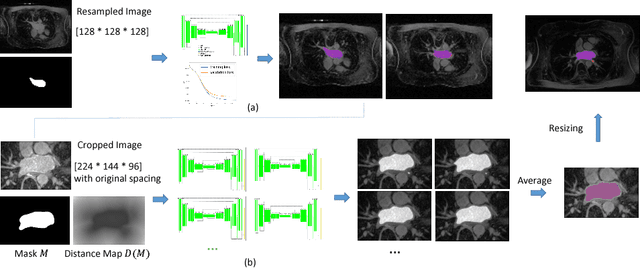
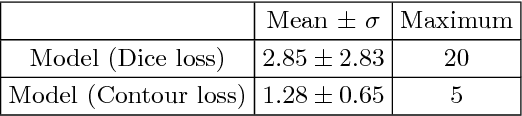
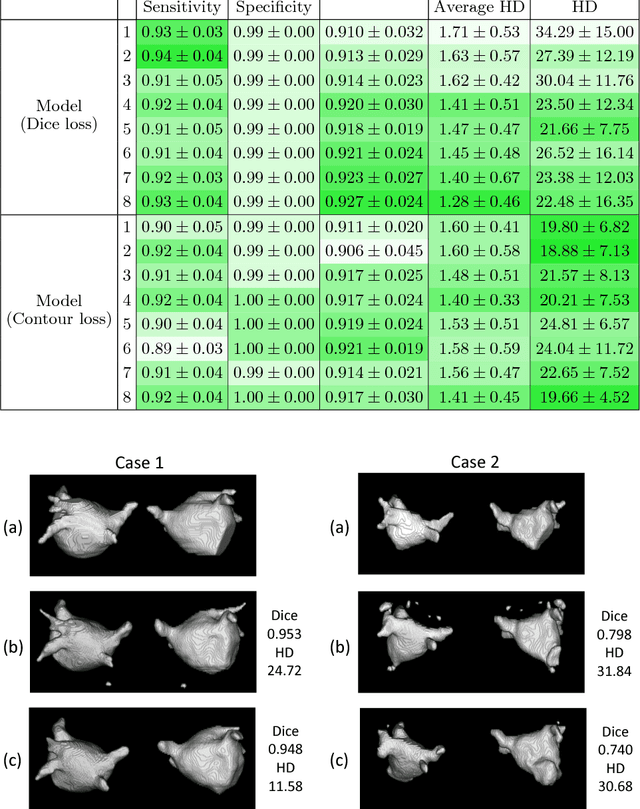
Radiological imaging offers effective measurement of anatomy, which is useful in disease diagnosis and assessment. Previous study has shown that the left atrial wall remodeling can provide information to predict treatment outcome in atrial fibrillation. Nevertheless, the segmentation of the left atrial structures from medical images is still very time-consuming. Current advances in neural network may help creating automatic segmentation models that reduce the workload for clinicians. In this preliminary study, we propose automated, two-stage, three-dimensional U-Nets with convolutional neural network, for the challenging task of left atrial segmentation. Unlike previous two-dimensional image segmentation methods, we use 3D U-Nets to obtain the heart cavity directly in 3D. The dual 3D U-Net structure consists of, a first U-Net to coarsely segment and locate the left atrium, and a second U-Net to accurately segment the left atrium under higher resolution. In addition, we introduce a Contour loss based on additional distance information to adjust the final segmentation. We randomly split the data into training datasets (80 subjects) and validation datasets (20 subjects) to train multiple models, with different augmentation setting. Experiments show that the average Dice coefficients for validation datasets are around 0.91 - 0.92, the sensitivity around 0.90-0.94 and the specificity 0.99. Compared with traditional Dice loss, models trained with Contour loss in general offer smaller Hausdorff distance with similar Dice coefficient, and have less connected components in predictions. Finally, we integrate several trained models in an ensemble prediction to segment testing datasets.

geomstats: a Python Package for Riemannian Geometry in Machine Learning

We introduce geomstats, a python package that performs computations on manifolds such as hyperspheres, hyperbolic spaces, spaces of symmetric positive definite matrices and Lie groups of transformations. We provide efficient and extensively unit-tested implementations of these manifolds, together with useful Riemannian metrics and associated Exponential and Logarithm maps. The corresponding geodesic distances provide a range of intuitive choices of Machine Learning loss functions. We also give the corresponding Riemannian gradients. The operations implemented in geomstats are available with different computing backends such as numpy, tensorflow and keras. We have enabled GPU implementation and integrated geomstats manifold computations into keras deep learning framework. This paper also presents a review of manifolds in machine learning and an overview of the geomstats package with examples demonstrating its use for efficient and user-friendly Riemannian geometry.