Optical matrix imaging applied to embryology

High-resolution label-free imaging of oocytes and embryos is essential for in vitro fertilization procedures. Yet conventional microscopy fails in this task because of aberrations and multiple scattering induced by refractive index heterogeneities inside the sample. These detrimental phenomena drastically degrade the images of early embryos particularly in depth. To overcome these fundamental problems without sacrificing the frame rate, optical matrix imaging (OMI) is a suitable tool. Relying on an ultra-fast measurement of the reflection matrix associated with the sample, it can compensate for aberration and forward multiple scattering in post-processing, thereby providing three-dimensional and highly contrasted images of embryos at a confocal resolution. As a first proof-of-concept, bovine oocytes and embryos are imaged at a 300 nm resolution almost in real time. Our system enables visualization of intracellular structures such as lipids and mitochondria in the cytoplasm or the zona pellucida surrounding it. Altogether, we demonstrate that OMI is a promising tool for research in developmental biology and for time-lapse monitoring of oocytes and embryos in assisted reproduction.

Multi-Spectral Reflection Matrix for Ultra-Fast 3D Label-Free Microscopy

Label-free microscopy exploits light scattering to obtain a three-dimensional image of biological tissues. However, light propagation is affected by aberrations and multiple scattering, which drastically degrade the image quality and limit the penetration depth. Multi-conjugate adaptive optics and time-gated matrix approaches have been developed to compensate for aberrations but the associated frame rate is extremely limited for 3D imaging. Here we develop a multi-spectral matrix approach to solve these fundamental problems. Based on an interferometric measurement of a polychromatic reflection matrix, the focusing process can be optimized in post-processing at any voxel by addressing independently each frequency component of the wave-field. A proof-of-concept experiment demonstrates the three-dimensional image of an opaque human cornea over a 0.1 mm^3-field-of-view at a 290 nm-resolution and a 1 Hz-frame rate. This work paves the way towards a fully-digital microscope allowing real-time, in-vivo, quantitative and deep inspection of tissues.

Cardiac Motion Modeling with Parallel Transport and Shape Splines

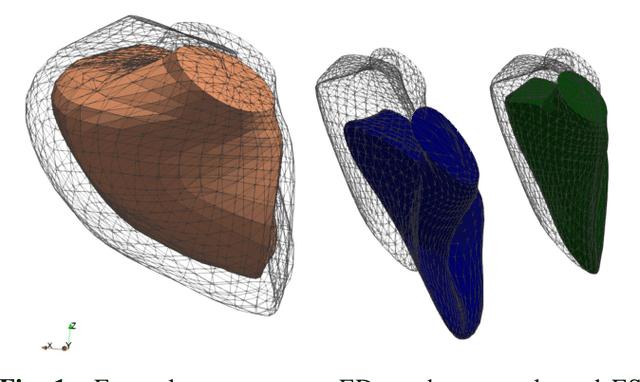
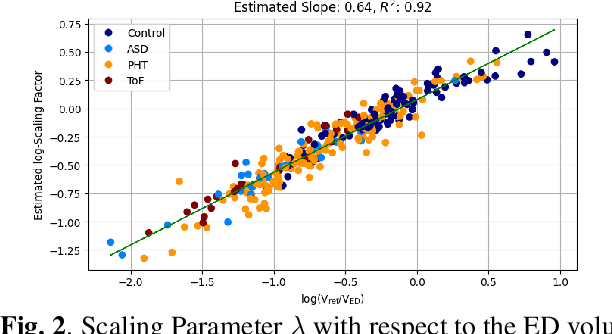
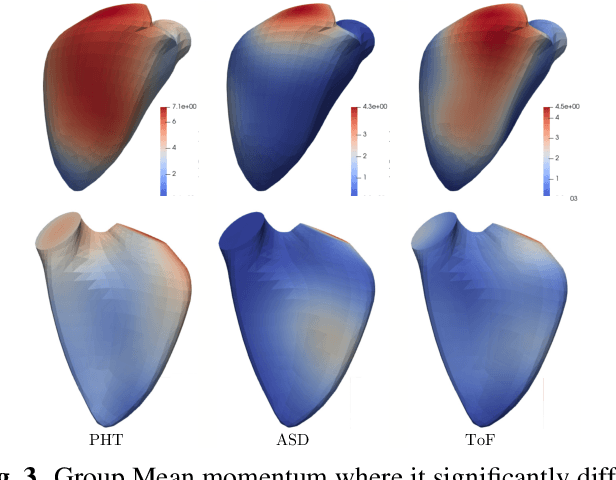
In cases of pressure or volume overload, probing cardiac function may be difficult because of the interactions between shape and deformations.In this work, we use the LDDMM framework and parallel transport to estimate and reorient deformations of the right ventricle. We then propose a normalization procedure for the amplitude of the deformation, and a second-order spline model to represent the full cardiac contraction. The method is applied to 3D meshes of the right ventricle extracted from echocardiographic sequences of 314 patients divided into three disease categories and a control group. We find significant differences between pathologies in the model parameters, revealing insights into the dynamics of each disease.

Classifying histograms of medical data using information geometry of beta distributions

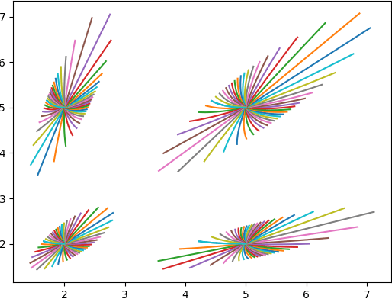
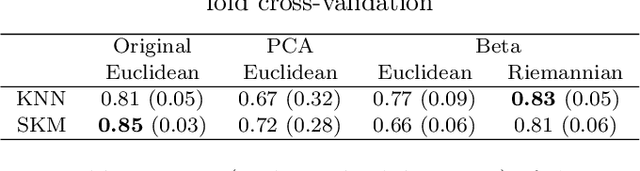
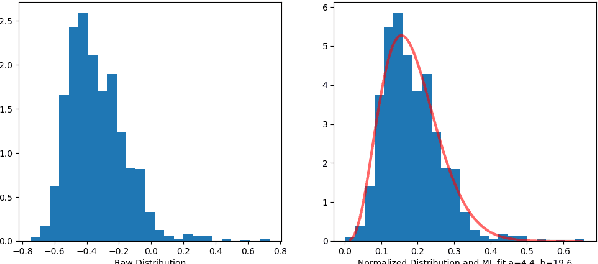
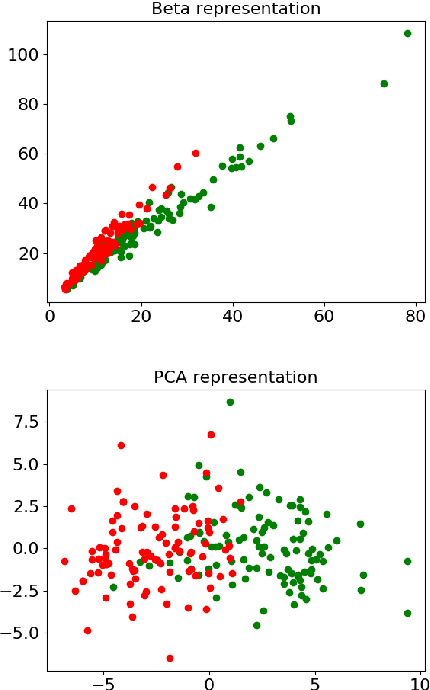
In this paper, we use tools of information geometry to compare, average and classify histograms. Beta distributions are fitted to the histograms and the corresponding Fisher information geometry is used for comparison. We show that this geometry is negatively curved, which guarantees uniqueness of the notion of mean, and makes it suitable to classify histograms through the popular K-means algorithm. We illustrate the use of these geometric tools in supervised and unsupervised classification procedures of two medical data-sets, cardiac shape deformations for the detection of pulmonary hypertension and brain cortical thickness for the diagnosis of Alzheimer's disease.

Geomstats: A Python Package for Riemannian Geometry in Machine Learning

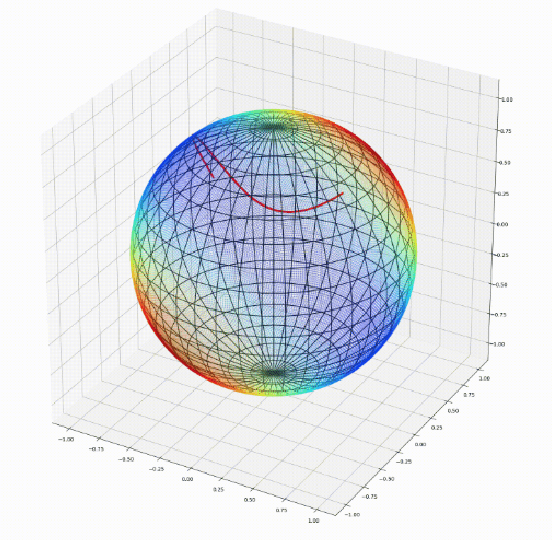
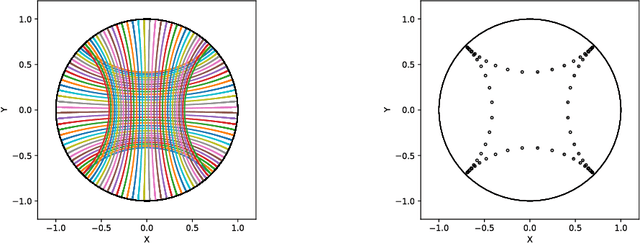
We introduce Geomstats, an open-source Python toolbox for computations and statistics on nonlinear manifolds, such as hyperbolic spaces, spaces of symmetric positive definite matrices, Lie groups of transformations, and many more. We provide object-oriented and extensively unit-tested implementations. Among others, manifolds come equipped with families of Riemannian metrics, with associated exponential and logarithmic maps, geodesics and parallel transport. Statistics and learning algorithms provide methods for estimation, clustering and dimension reduction on manifolds. All associated operations are vectorized for batch computation and provide support for different execution backends, namely NumPy, PyTorch and TensorFlow, enabling GPU acceleration. This paper presents the package, compares it with related libraries and provides relevant code examples. We show that Geomstats provides reliable building blocks to foster research in differential geometry and statistics, and to democratize the use of Riemannian geometry in machine learning applications. The source code is freely available under the MIT license at \url{geomstats.ai}.