Classifying histograms of medical data using information geometry of beta distributions

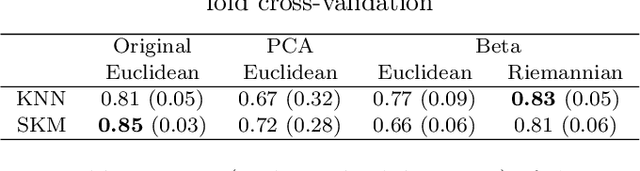
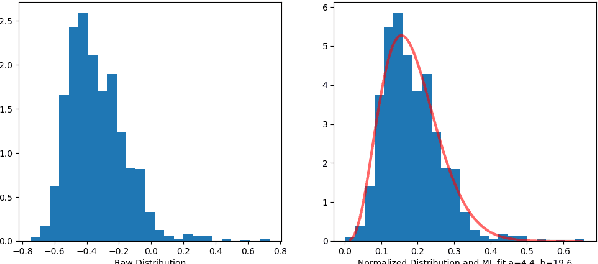
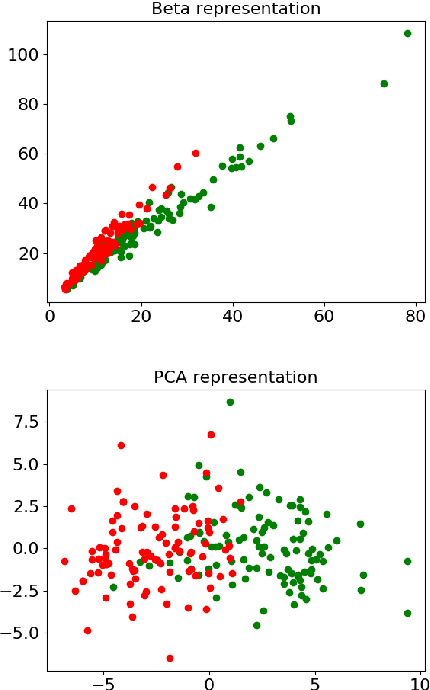
In this paper, we use tools of information geometry to compare, average and classify histograms. Beta distributions are fitted to the histograms and the corresponding Fisher information geometry is used for comparison. We show that this geometry is negatively curved, which guarantees uniqueness of the notion of mean, and makes it suitable to classify histograms through the popular K-means algorithm. We illustrate the use of these geometric tools in supervised and unsupervised classification procedures of two medical data-sets, cardiac shape deformations for the detection of pulmonary hypertension and brain cortical thickness for the diagnosis of Alzheimer's disease.