Local Max-Entropy and Free Energy Principles, Belief Diffusions and their Singularities

A comprehensive picture of three Bethe-Kikuchi variational principles including their relationship to belief propagation (BP) algorithms on hypergraphs is given. The structure of BP equations is generalized to define continuous-time diffusions, solving localized versions of the max-entropy principle (A), the variational free energy principle (B), and a less usual equilibrium free energy principle (C), Legendre dual to A. Both critical points of Bethe-Kikuchi functionals and stationary beliefs are shown to lie at the non-linear intersection of two constraint surfaces, enforcing energy conservation and marginal consistency respectively. The hypersurface of singular beliefs, accross which equilibria become unstable as the constraint surfaces meet tangentially, is described by polynomial equations in the convex polytope of consistent beliefs. This polynomial is expressed by a loop series expansion for graphs of binary variables.

Equivariant Message Passing Neural Network for Crystal Material Discovery

Automatic material discovery with desired properties is a fundamental challenge for material sciences. Considerable attention has recently been devoted to generating stable crystal structures. While existing work has shown impressive success on supervised tasks such as property prediction, the progress on unsupervised tasks such as material generation is still hampered by the limited extent to which the equivalent geometric representations of the same crystal are considered. To address this challenge, we propose EMPNN a periodic equivariant message-passing neural network that learns crystal lattice deformation in an unsupervised fashion. Our model equivalently acts on lattice according to the deformation action that must be performed, making it suitable for crystal generation, relaxation and optimisation. We present experimental evaluations that demonstrate the effectiveness of our approach.

Local Max-Entropy and Free Energy Principles Solved by Belief Propagation

A statistical system is classically defined on a set of microstates $E$ by a global energy function $H : E \to \mathbb{R}$, yielding Gibbs probability measures (softmins) $\rho^\beta(H)$ for every inverse temperature $\beta = T^{-1}$. Gibbs states are simultaneously characterized by free energy principles and the max-entropy principle, with dual constraints on inverse temperature $\beta$ and mean energy ${\cal U}(\beta) = \mathbb{E}_{\rho^\beta}[H]$ respectively. The Legendre transform relates these diverse variational principles which are unfortunately not tractable in high dimension. The global energy is generally given as a sum $H(x) = \sum_{\rm a \subset \Omega} h_{\rm a}(x_{|\rm a})$ of local short-range interactions $h_{\rm a} : E_{\rm a} \to \mathbb{R}$ indexed by bounded subregions ${\rm a} \subset \Omega$, and this local structure can be used to design good approximation schemes on thermodynamic functionals. We show that the generalized belief propagation (GBP) algorithm solves a collection of local variational principles, by converging to critical points of Bethe-Kikuchi approximations of the free energy $F(\beta)$, the Shannon entropy $S(\cal U)$, and the variational free energy ${\cal F}(\beta) = {\cal U} - \beta^{-1} S(\cal U)$, extending an initial correspondence by Yedidia et al. This local form of Legendre duality yields a possible degenerate relationship between mean energy ${\cal U}$ and $\beta$.

Belief Propagation as Diffusion

We introduce novel belief propagation algorithms to estimate the marginals of a high dimensional probability distribution. They involve natural (co)homological constructions relevant for a localised description of statistical systems.

Geomstats: A Python Package for Riemannian Geometry in Machine Learning

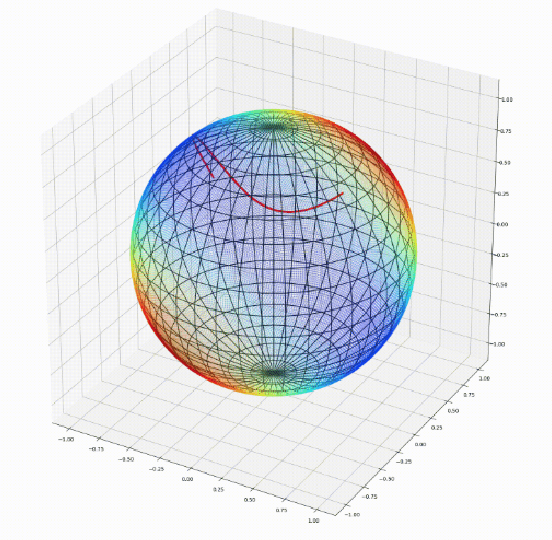
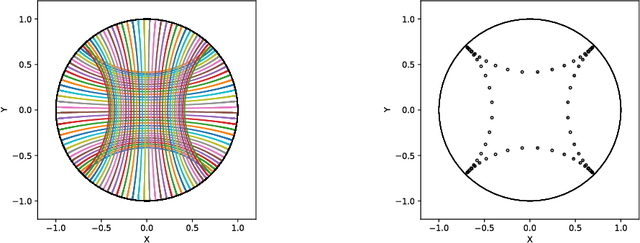
We introduce Geomstats, an open-source Python toolbox for computations and statistics on nonlinear manifolds, such as hyperbolic spaces, spaces of symmetric positive definite matrices, Lie groups of transformations, and many more. We provide object-oriented and extensively unit-tested implementations. Among others, manifolds come equipped with families of Riemannian metrics, with associated exponential and logarithmic maps, geodesics and parallel transport. Statistics and learning algorithms provide methods for estimation, clustering and dimension reduction on manifolds. All associated operations are vectorized for batch computation and provide support for different execution backends, namely NumPy, PyTorch and TensorFlow, enabling GPU acceleration. This paper presents the package, compares it with related libraries and provides relevant code examples. We show that Geomstats provides reliable building blocks to foster research in differential geometry and statistics, and to democratize the use of Riemannian geometry in machine learning applications. The source code is freely available under the MIT license at \url{geomstats.ai}.