Geomstats: A Python Package for Riemannian Geometry in Machine Learning

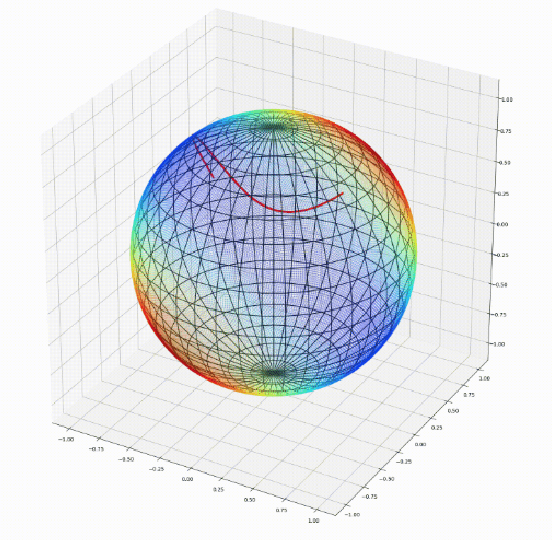
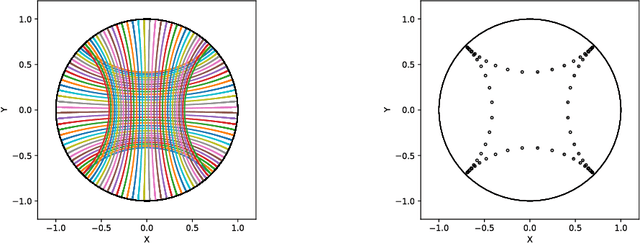
We introduce Geomstats, an open-source Python toolbox for computations and statistics on nonlinear manifolds, such as hyperbolic spaces, spaces of symmetric positive definite matrices, Lie groups of transformations, and many more. We provide object-oriented and extensively unit-tested implementations. Among others, manifolds come equipped with families of Riemannian metrics, with associated exponential and logarithmic maps, geodesics and parallel transport. Statistics and learning algorithms provide methods for estimation, clustering and dimension reduction on manifolds. All associated operations are vectorized for batch computation and provide support for different execution backends, namely NumPy, PyTorch and TensorFlow, enabling GPU acceleration. This paper presents the package, compares it with related libraries and provides relevant code examples. We show that Geomstats provides reliable building blocks to foster research in differential geometry and statistics, and to democratize the use of Riemannian geometry in machine learning applications. The source code is freely available under the MIT license at \url{geomstats.ai}.

Learning graph-structured data using Poincaré embeddings and Riemannian K-means algorithms

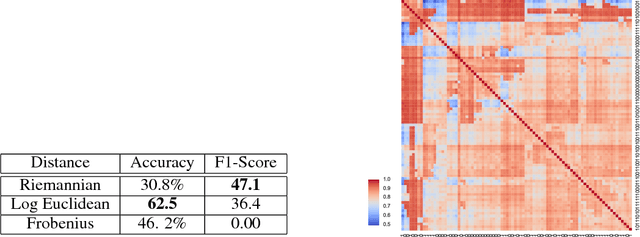
Recent literature has shown several benefits of hyperbolic embedding of graph-structured data (GSD) in representing their structures and latent relations. While several studies have explored the ability of hyperbolic embedding to represent data (for example, by quantifying their mean average precision) and their ability to produce better visualisations of clusters, only few works exploited the effectiveness of hyperbolic embedding to perform learning on the initial GSD. Motivated by innovative ideas from the fields of Brain computer interfaces and Radar processing, this paper presents a new scheme for learning GSD based on hyperbolic embedding, Riemannian barycentre (i.e. Fr\'echet or geometric mean) and $K$-means algorithms as a significant tool that derives from it. The main idea is as follows. Relying on the Riemannian barycentre, we define a notion of minimal variance which allows us to choose an embedding between different ones. This embedding is used thereafter together with $K$-means algorithms to perform unsupervised clustering and in combination with the nearest neighbour rule to perform supervised learning. We demonstrate the performance of the proposed framework through several experiments on real-world social networks and hierarchical GSD. The obtained results outperform their counterparts in high-dimensional Euclidean spaces and recent proposed geometric approaches.