Reward-Preserving Attacks For Robust Reinforcement Learning

Adversarial robustness in RL is difficult because perturbations affect entire trajectories: strong attacks can break learning, while weak attacks yield little robustness, and the appropriate strength varies by state. We propose $α$-reward-preserving attacks, which adapt the strength of the adversary so that an $α$ fraction of the nominal-to-worst-case return gap remains achievable at each state. In deep RL, we use a gradient-based attack direction and learn a state-dependent magnitude $η\le η_{\mathcal B}$ selected via a critic $Q^π_α((s,a),η)$ trained off-policy over diverse radii. This adaptive tuning calibrates attack strength and, with intermediate $α$, improves robustness across radii while preserving nominal performance, outperforming fixed- and random-radius baselines.

Towards stable AI systems for Evaluating Arabic Pronunciations

Modern Arabic ASR systems such as wav2vec 2.0 excel at word- and sentence-level transcription, yet struggle to classify isolated letters. In this study, we show that this phoneme-level task, crucial for language learning, speech therapy, and phonetic research, is challenging because isolated letters lack co-articulatory cues, provide no lexical context, and last only a few hundred milliseconds. Recogniser systems must therefore rely solely on variable acoustic cues, a difficulty heightened by Arabic's emphatic (pharyngealized) consonants and other sounds with no close analogues in many languages. This study introduces a diverse, diacritised corpus of isolated Arabic letters and demonstrates that state-of-the-art wav2vec 2.0 models achieve only 35% accuracy on it. Training a lightweight neural network on wav2vec embeddings raises performance to 65%. However, adding a small amplitude perturbation (epsilon = 0.05) cuts accuracy to 32%. To restore robustness, we apply adversarial training, limiting the noisy-speech drop to 9% while preserving clean-speech accuracy. We detail the corpus, training pipeline, and evaluation protocol, and release, on demand, data and code for reproducibility. Finally, we outline future work extending these methods to word- and sentence-level frameworks, where precise letter pronunciation remains critical.

Robust Deep Reinforcement Learning Through Adversarial Attacks and Training : A Survey

Deep Reinforcement Learning (DRL) is an approach for training autonomous agents across various complex environments. Despite its significant performance in well known environments, it remains susceptible to minor conditions variations, raising concerns about its reliability in real-world applications. To improve usability, DRL must demonstrate trustworthiness and robustness. A way to improve robustness of DRL to unknown changes in the conditions is through Adversarial Training, by training the agent against well suited adversarial attacks on the dynamics of the environment. Addressing this critical issue, our work presents an in-depth analysis of contemporary adversarial attack methodologies, systematically categorizing them and comparing their objectives and operational mechanisms. This classification offers a detailed insight into how adversarial attacks effectively act for evaluating the resilience of DRL agents, thereby paving the way for enhancing their robustness.

SEEDS: Exponential SDE Solvers for Fast High-Quality Sampling from Diffusion Models

A potent class of generative models known as Diffusion Probabilistic Models (DPMs) has become prominent. A forward diffusion process adds gradually noise to data, while a model learns to gradually denoise. Sampling from pre-trained DPMs is obtained by solving differential equations (DE) defined by the learnt model, a process which has shown to be prohibitively slow. Numerous efforts on speeding-up this process have consisted on crafting powerful ODE solvers. Despite being quick, such solvers do not usually reach the optimal quality achieved by available slow SDE solvers. Our goal is to propose SDE solvers that reach optimal quality without requiring several hundreds or thousands of NFEs to achieve that goal. In this work, we propose Stochastic Exponential Derivative-free Solvers (SEEDS), improving and generalizing Exponential Integrator approaches to the stochastic case on several frameworks. After carefully analyzing the formulation of exact solutions of diffusion SDEs, we craft SEEDS to analytically compute the linear part of such solutions. Inspired by the Exponential Time-Differencing method, SEEDS uses a novel treatment of the stochastic components of solutions, enabling the analytical computation of their variance, and contains high-order terms allowing to reach optimal quality sampling $\sim3$-$5\times$ faster than previous SDE methods. We validate our approach on several image generation benchmarks, showing that SEEDS outperforms or is competitive with previous SDE solvers. Contrary to the latter, SEEDS are derivative and training free, and we fully prove strong convergence guarantees for them.

Riemannian data-dependent randomized smoothing for neural networks certification

Certification of neural networks is an important and challenging problem that has been attracting the attention of the machine learning community since few years. In this paper, we focus on randomized smoothing (RS) which is considered as the state-of-the-art method to obtain certifiably robust neural networks. In particular, a new data-dependent RS technique called ANCER introduced recently can be used to certify ellipses with orthogonal axis near each input data of the neural network. In this work, we remark that ANCER is not invariant under rotation of input data and propose a new rotationally-invariant formulation of it which can certify ellipses without constraints on their axis. Our approach called Riemannian Data Dependant Randomized Smoothing (RDDRS) relies on information geometry techniques on the manifold of covariance matrices and can certify bigger regions than ANCER based on our experiments on the MNIST dataset.

Noisy Learning for Neural ODEs Acts as a Robustness Locus Widening

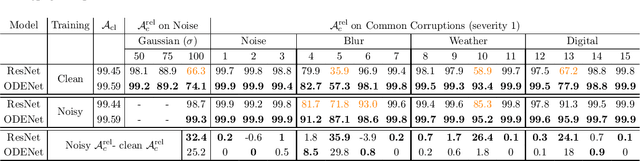
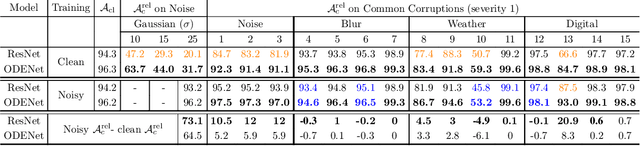
We investigate the problems and challenges of evaluating the robustness of Differential Equation-based (DE) networks against synthetic distribution shifts. We propose a novel and simple accuracy metric which can be used to evaluate intrinsic robustness and to validate dataset corruption simulators. We also propose methodology recommendations, destined for evaluating the many faces of neural DEs' robustness and for comparing them with their discrete counterparts rigorously. We then use this criteria to evaluate a cheap data augmentation technique as a reliable way for demonstrating the natural robustness of neural ODEs against simulated image corruptions across multiple datasets.

Realization Theory Of Recurrent Neural ODEs Using Polynomial System Embeddings

In this paper we show that neural ODE analogs of recurrent (ODE-RNN) and Long Short-Term Memory (ODE-LSTM) networks can be algorithmically embeddeded into the class of polynomial systems. This embedding preserves input-output behavior and can suitably be extended to other neural DE architectures. We then use realization theory of polynomial systems to provide necessary conditions for an input-output map to be realizable by an ODE-LSTM and sufficient conditions for minimality of such systems. These results represent the first steps towards realization theory of recurrent neural ODE architectures, which is is expected be useful for model reduction and learning algorithm analysis of recurrent neural ODEs.

Improving Robustness of Deep Reinforcement Learning Agents: Environment Attacks based on Critic Networks

To improve policy robustness of deep reinforcement learning agents, a line of recent works focus on producing disturbances of the environment. Existing approaches of the literature to generate meaningful disturbances of the environment are adversarial reinforcement learning methods. These methods set the problem as a two-player game between the protagonist agent, which learns to perform a task in an environment, and the adversary agent, which learns to disturb the protagonist via modifications of the considered environment. Both protagonist and adversary are trained with deep reinforcement learning algorithms. Alternatively, we propose in this paper to build on gradient-based adversarial attacks, usually used for classification tasks for instance, that we apply on the critic network of the protagonist to identify efficient disturbances of the environment. Rather than learning an attacker policy, which usually reveals as very complex and unstable, we leverage the knowledge of the critic network of the protagonist, to dynamically complexify the task at each step of the learning process. We show that our method, while being faster and lighter, leads to significantly better improvements in policy robustness than existing methods of the literature.

Stochastic sparse adversarial attacks

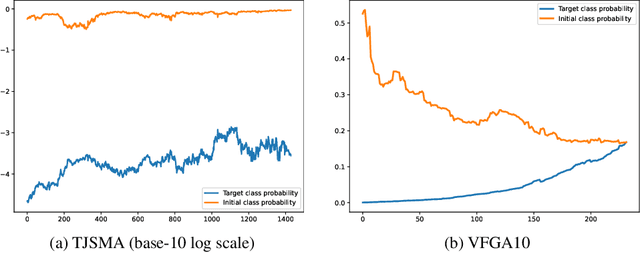
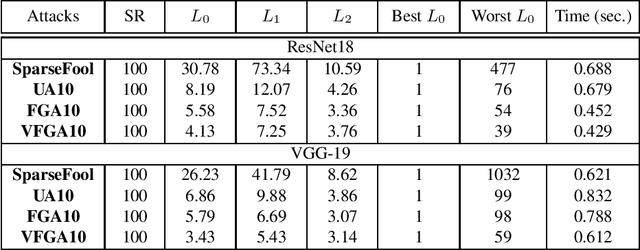
Adversarial attacks of neural network classifiers (NNC) and the use of random noises in these methods have stimulated a large number of works in recent years. However, despite all the previous investigations, existing approaches that rely on random noises to fool NNC have fallen far short of the-state-of-the-art adversarial methods performances. In this paper, we fill this gap by introducing stochastic sparse adversarial attacks (SSAA), standing as simple, fast and purely noise-based targeted and untargeted attacks of NNC. SSAA offer new examples of sparse (or $L_0$) attacks for which only few methods have been proposed previously. These attacks are devised by exploiting a small-time expansion idea widely used for Markov processes. Experiments on small and large datasets (CIFAR-10 and ImageNet) illustrate several advantages of SSAA in comparison with the-state-of-the-art methods. For instance, in the untargeted case, our method called voting folded Gaussian attack (VFGA) scales efficiently to ImageNet and achieves a significantly lower $L_0$ score than SparseFool (up to $\frac{1}{14}$ lower) while being faster. In the targeted setting, VFGA achives appealing results on ImageNet and is significantly much faster than Carlini-Wagner $L_0$ attack.

Probabilistic Jacobian-based Saliency Maps Attacks

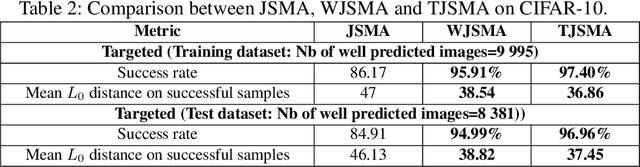
Machine learning models have achieved spectacular performances in various critical fields including intelligent monitoring, autonomous driving and malware detection. Therefore, robustness against adversarial attacks represents a key issue to trust these models. In particular, the Jacobian-based Saliency Map Attack (JSMA) is widely used to fool neural network classifiers. In this paper, we introduce Weighted JSMA (WJSMA) and Taylor JSMA (TJSMA), simple, faster and more efficient versions of JSMA. These attacks rely upon new saliency maps involving the neural network Jacobian, its output probabilities and the input features. We demonstrate the advantages of WJSMA and TJSMA through two computer vision applications on 1) LeNet-5, a well-known Neural Network classifier (NNC), on the MNIST database and on 2) a more challenging NNC on the CIFAR-10 dataset. We obtain that WJSMA and TJSMA significantly outperform JSMA in success rate, speed and average number of changed features. For instance, on LeNet-5 (with $100\%$ and $99.49\%$ accuracies on the training and test sets), WJSMA and TJSMA respectively exceed $97\%$ and $98.60\%$ in success rate for a maximum authorised distortion of $14.5\%$, outperforming JSMA with more than $9.5$ and $11$ percentage points. The new attacks are then used to defend and create more robust models than those trained against JSMA. Like JSMA, our attacks are not scalable on large datasets such as IMAGENET but despite this fact, they remain attractive for relatively small datasets like MNIST, CIFAR-10 and may be potential tools for future applications.