Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
Loic Cantat
Noisy Learning for Neural ODEs Acts as a Robustness Locus Widening
Jun 16, 2022Figures and Tables: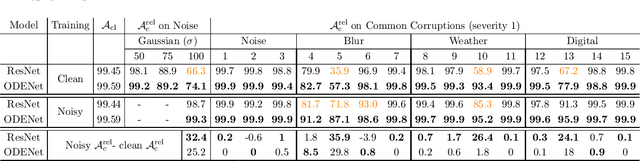


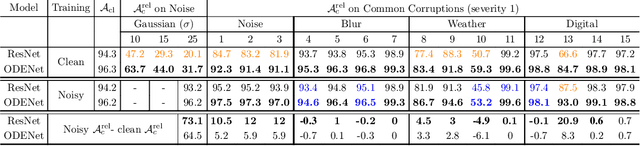




Abstract:We investigate the problems and challenges of evaluating the robustness of Differential Equation-based (DE) networks against synthetic distribution shifts. We propose a novel and simple accuracy metric which can be used to evaluate intrinsic robustness and to validate dataset corruption simulators. We also propose methodology recommendations, destined for evaluating the many faces of neural DEs' robustness and for comparing them with their discrete counterparts rigorously. We then use this criteria to evaluate a cheap data augmentation technique as a reliable way for demonstrating the natural robustness of neural ODEs against simulated image corruptions across multiple datasets.
* Accepted at ICLM 2022 Workshop "PODS"
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge