Detecting and Defending Against Adversarial Attacks on Automatic Speech Recognition via Diffusion Models

Automatic speech recognition (ASR) systems are known to be vulnerable to adversarial attacks. This paper addresses detection and defence against targeted white-box attacks on speech signals for ASR systems. While existing work has utilised diffusion models (DMs) to purify adversarial examples, achieving state-of-the-art results in keyword spotting tasks, their effectiveness for more complex tasks such as sentence-level ASR remains unexplored. Additionally, the impact of the number of forward diffusion steps on performance is not well understood. In this paper, we systematically investigate the use of DMs for defending against adversarial attacks on sentences and examine the effect of varying forward diffusion steps. Through comprehensive experiments on the Mozilla Common Voice dataset, we demonstrate that two forward diffusion steps can completely defend against adversarial attacks on sentences. Moreover, we introduce a novel, training-free approach for detecting adversarial attacks by leveraging a pre-trained DM. Our experimental results show that this method can detect adversarial attacks with high accuracy.

A finite-sample generalization bound for stable LPV systems

One of the main theoretical challenges in learning dynamical systems from data is providing upper bounds on the generalization error, that is, the difference between the expected prediction error and the empirical prediction error measured on some finite sample. In machine learning, a popular class of such bounds are the so-called Probably Approximately Correct (PAC) bounds. In this paper, we derive a PAC bound for stable continuous-time linear parameter-varying (LPV) systems. Our bound depends on the H2 norm of the chosen class of the LPV systems, but does not depend on the time interval for which the signals are considered.

SEEDS: Exponential SDE Solvers for Fast High-Quality Sampling from Diffusion Models

A potent class of generative models known as Diffusion Probabilistic Models (DPMs) has become prominent. A forward diffusion process adds gradually noise to data, while a model learns to gradually denoise. Sampling from pre-trained DPMs is obtained by solving differential equations (DE) defined by the learnt model, a process which has shown to be prohibitively slow. Numerous efforts on speeding-up this process have consisted on crafting powerful ODE solvers. Despite being quick, such solvers do not usually reach the optimal quality achieved by available slow SDE solvers. Our goal is to propose SDE solvers that reach optimal quality without requiring several hundreds or thousands of NFEs to achieve that goal. In this work, we propose Stochastic Exponential Derivative-free Solvers (SEEDS), improving and generalizing Exponential Integrator approaches to the stochastic case on several frameworks. After carefully analyzing the formulation of exact solutions of diffusion SDEs, we craft SEEDS to analytically compute the linear part of such solutions. Inspired by the Exponential Time-Differencing method, SEEDS uses a novel treatment of the stochastic components of solutions, enabling the analytical computation of their variance, and contains high-order terms allowing to reach optimal quality sampling $\sim3$-$5\times$ faster than previous SDE methods. We validate our approach on several image generation benchmarks, showing that SEEDS outperforms or is competitive with previous SDE solvers. Contrary to the latter, SEEDS are derivative and training free, and we fully prove strong convergence guarantees for them.

Software-defined Optoacoustic Tomography

In this work we present the first application of software-defined optoelectronics (SDO) for bidimensional optoacoustic tomography (OAT). The SDO concept refers to optoelectronic systems where the functionality associated with the conditioning and processing of optical and electrical signals are digitally implemented and controlled by software. This paradigm takes advantage of the flexibility of software-defined hardware platforms to develop adaptive instrumentation systems. We implement an OAT system based on a heterodyne interferometer in a Mach-Zehnder configuration and a commercial software-defined radio platform (SDR). Here the SDR serves as a function generator and oscilloscope at the same time providing perfect carrier synchronization between its transmitter and receiver in a coherent baseband modulator scheme. Therefore, the carrier synchronization enables us to have a much better phase recovery. We study the performance of the OAT SDO system by means of different bidimensional phantoms and the analysis of the reconstructed images.

Noisy Learning for Neural ODEs Acts as a Robustness Locus Widening

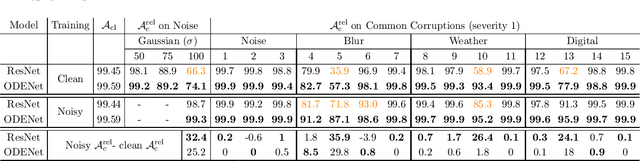
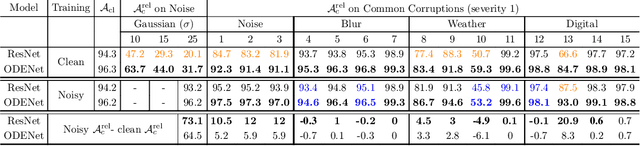
We investigate the problems and challenges of evaluating the robustness of Differential Equation-based (DE) networks against synthetic distribution shifts. We propose a novel and simple accuracy metric which can be used to evaluate intrinsic robustness and to validate dataset corruption simulators. We also propose methodology recommendations, destined for evaluating the many faces of neural DEs' robustness and for comparing them with their discrete counterparts rigorously. We then use this criteria to evaluate a cheap data augmentation technique as a reliable way for demonstrating the natural robustness of neural ODEs against simulated image corruptions across multiple datasets.

Realization Theory Of Recurrent Neural ODEs Using Polynomial System Embeddings

In this paper we show that neural ODE analogs of recurrent (ODE-RNN) and Long Short-Term Memory (ODE-LSTM) networks can be algorithmically embeddeded into the class of polynomial systems. This embedding preserves input-output behavior and can suitably be extended to other neural DE architectures. We then use realization theory of polynomial systems to provide necessary conditions for an input-output map to be realizable by an ODE-LSTM and sufficient conditions for minimality of such systems. These results represent the first steps towards realization theory of recurrent neural ODE architectures, which is is expected be useful for model reduction and learning algorithm analysis of recurrent neural ODEs.