NeurIPS 2025 E2LM Competition : Early Training Evaluation of Language Models

Existing benchmarks have proven effective for assessing the performance of fully trained large language models. However, we find striking differences in the early training stages of small models, where benchmarks often fail to provide meaningful or discriminative signals. To explore how these differences arise, this competition tackles the challenge of designing scientific knowledge evaluation tasks specifically tailored for measuring early training progress of language models. Participants are invited to develop novel evaluation methodologies or adapt existing benchmarks to better capture performance differences among language models. To support this effort, we provide three pre-trained small models (0.5B, 1B, and 3B parameters), along with intermediate checkpoints sampled during training up to 200B tokens. All experiments and development work can be run on widely available free cloud-based GPU platforms, making participation accessible to researchers with limited computational resources. Submissions will be evaluated based on three criteria: the quality of the performance signal they produce, the consistency of model rankings at 1 trillion tokens of training, and their relevance to the scientific knowledge domain. By promoting the design of tailored evaluation strategies for early training, this competition aims to attract a broad range of participants from various disciplines, including those who may not be machine learning experts or have access to dedicated GPU resources. Ultimately, this initiative seeks to make foundational LLM research more systematic and benchmark-informed from the earliest phases of model development.

ENMA: Tokenwise Autoregression for Generative Neural PDE Operators

Solving time-dependent parametric partial differential equations (PDEs) remains a fundamental challenge for neural solvers, particularly when generalizing across a wide range of physical parameters and dynamics. When data is uncertain or incomplete-as is often the case-a natural approach is to turn to generative models. We introduce ENMA, a generative neural operator designed to model spatio-temporal dynamics arising from physical phenomena. ENMA predicts future dynamics in a compressed latent space using a generative masked autoregressive transformer trained with flow matching loss, enabling tokenwise generation. Irregularly sampled spatial observations are encoded into uniform latent representations via attention mechanisms and further compressed through a spatio-temporal convolutional encoder. This allows ENMA to perform in-context learning at inference time by conditioning on either past states of the target trajectory or auxiliary context trajectories with similar dynamics. The result is a robust and adaptable framework that generalizes to new PDE regimes and supports one-shot surrogate modeling of time-dependent parametric PDEs.

UP-ROM : Uncertainty-Aware and Parametrised dynamic Reduced-Order Model, application to unsteady flows

Reduced order models (ROMs) play a critical role in fluid mechanics by providing low-cost predictions, making them an attractive tool for engineering applications. However, for ROMs to be widely applicable, they must not only generalise well across different regimes, but also provide a measure of confidence in their predictions. While recent data-driven approaches have begun to address nonlinear reduction techniques to improve predictions in transient environments, challenges remain in terms of robustness and parametrisation. In this work, we present a nonlinear reduction strategy specifically designed for transient flows that incorporates parametrisation and uncertainty quantification. Our reduction strategy features a variational auto-encoder (VAE) that uses variational inference for confidence measurement. We use a latent space transformer that incorporates recent advances in attention mechanisms to predict dynamical systems. Attention's versatility in learning sequences and capturing their dependence on external parameters enhances generalisation across a wide range of dynamics. Prediction, coupled with confidence, enables more informed decision making and addresses the need for more robust models. In addition, this confidence is used to cost-effectively sample the parameter space, improving model performance a priori across the entire parameter space without requiring evaluation data for the entire domain.

SCOPE: A Self-supervised Framework for Improving Faithfulness in Conditional Text Generation

Large Language Models (LLMs), when used for conditional text generation, often produce hallucinations, i.e., information that is unfaithful or not grounded in the input context. This issue arises in typical conditional text generation tasks, such as text summarization and data-to-text generation, where the goal is to produce fluent text based on contextual input. When fine-tuned on specific domains, LLMs struggle to provide faithful answers to a given context, often adding information or generating errors. One underlying cause of this issue is that LLMs rely on statistical patterns learned from their training data. This reliance can interfere with the model's ability to stay faithful to a provided context, leading to the generation of ungrounded information. We build upon this observation and introduce a novel self-supervised method for generating a training set of unfaithful samples. We then refine the model using a training process that encourages the generation of grounded outputs over unfaithful ones, drawing on preference-based training. Our approach leads to significantly more grounded text generation, outperforming existing self-supervised techniques in faithfulness, as evaluated through automatic metrics, LLM-based assessments, and human evaluations.

GEPS: Boosting Generalization in Parametric PDE Neural Solvers through Adaptive Conditioning

Solving parametric partial differential equations (PDEs) presents significant challenges for data-driven methods due to the sensitivity of spatio-temporal dynamics to variations in PDE parameters. Machine learning approaches often struggle to capture this variability. To address this, data-driven approaches learn parametric PDEs by sampling a very large variety of trajectories with varying PDE parameters. We first show that incorporating conditioning mechanisms for learning parametric PDEs is essential and that among them, $\textit{adaptive conditioning}$, allows stronger generalization. As existing adaptive conditioning methods do not scale well with respect to the number of parameters to adapt in the neural solver, we propose GEPS, a simple adaptation mechanism to boost GEneralization in Pde Solvers via a first-order optimization and low-rank rapid adaptation of a small set of context parameters. We demonstrate the versatility of our approach for both fully data-driven and for physics-aware neural solvers. Validation performed on a whole range of spatio-temporal forecasting problems demonstrates excellent performance for generalizing to unseen conditions including initial conditions, PDE coefficients, forcing terms and solution domain. $\textit{Project page}$: https://geps-project.github.io

Learning a Neural Solver for Parametric PDE to Enhance Physics-Informed Methods

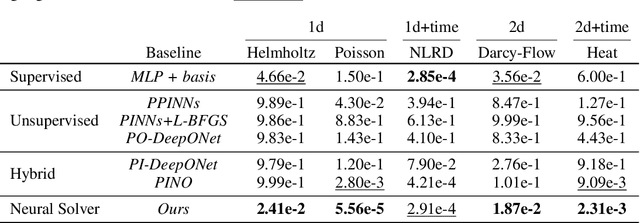
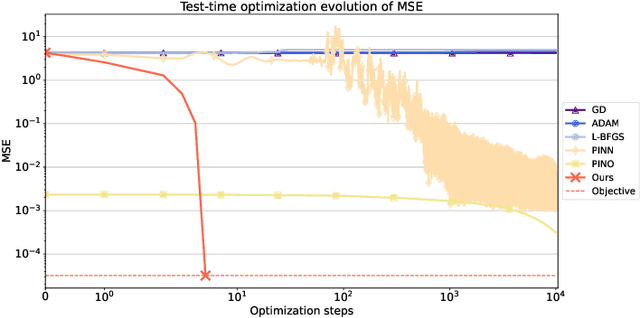
Physics-informed deep learning often faces optimization challenges due to the complexity of solving partial differential equations (PDEs), which involve exploring large solution spaces, require numerous iterations, and can lead to unstable training. These challenges arise particularly from the ill-conditioning of the optimization problem, caused by the differential terms in the loss function. To address these issues, we propose learning a solver, i.e., solving PDEs using a physics-informed iterative algorithm trained on data. Our method learns to condition a gradient descent algorithm that automatically adapts to each PDE instance, significantly accelerating and stabilizing the optimization process and enabling faster convergence of physics-aware models. Furthermore, while traditional physics-informed methods solve for a single PDE instance, our approach addresses parametric PDEs. Specifically, our method integrates the physical loss gradient with the PDE parameters to solve over a distribution of PDE parameters, including coefficients, initial conditions, or boundary conditions. We demonstrate the effectiveness of our method through empirical experiments on multiple datasets, comparing training and test-time optimization performance.

Probing Language Models on Their Knowledge Source

Large Language Models (LLMs) often encounter conflicts between their learned, internal (parametric knowledge, PK) and external knowledge provided during inference (contextual knowledge, CK). Understanding how LLMs models prioritize one knowledge source over the other remains a challenge. In this paper, we propose a novel probing framework to explore the mechanisms governing the selection between PK and CK in LLMs. Using controlled prompts designed to contradict the model's PK, we demonstrate that specific model activations are indicative of the knowledge source employed. We evaluate this framework on various LLMs of different sizes and demonstrate that mid-layer activations, particularly those related to relations in the input, are crucial in predicting knowledge source selection, paving the way for more reliable models capable of handling knowledge conflicts effectively.

Zebra: In-Context and Generative Pretraining for Solving Parametric PDEs

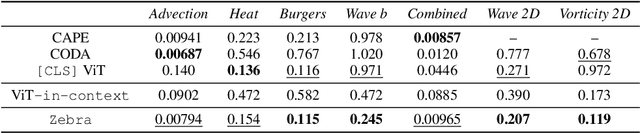
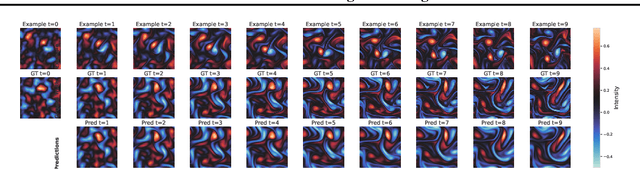
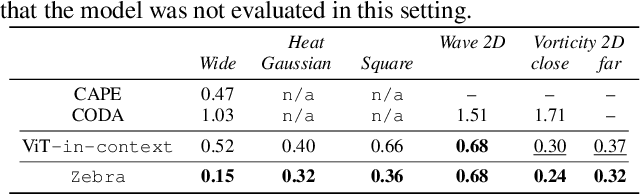
Solving time-dependent parametric partial differential equations (PDEs) is challenging, as models must adapt to variations in parameters such as coefficients, forcing terms, and boundary conditions. Data-driven neural solvers either train on data sampled from the PDE parameters distribution in the hope that the model generalizes to new instances or rely on gradient-based adaptation and meta-learning to implicitly encode the dynamics from observations. This often comes with increased inference complexity. Inspired by the in-context learning capabilities of large language models (LLMs), we introduce Zebra, a novel generative auto-regressive transformer designed to solve parametric PDEs without requiring gradient adaptation at inference. By leveraging in-context information during both pre-training and inference, Zebra dynamically adapts to new tasks by conditioning on input sequences that incorporate context trajectories or preceding states. This approach enables Zebra to flexibly handle arbitrarily sized context inputs and supports uncertainty quantification through the sampling of multiple solution trajectories. We evaluate Zebra across a variety of challenging PDE scenarios, demonstrating its adaptability, robustness, and superior performance compared to existing approaches.

NeurIPS 2024 ML4CFD Competition: Harnessing Machine Learning for Computational Fluid Dynamics in Airfoil Design

The integration of machine learning (ML) techniques for addressing intricate physics problems is increasingly recognized as a promising avenue for expediting simulations. However, assessing ML-derived physical models poses a significant challenge for their adoption within industrial contexts. This competition is designed to promote the development of innovative ML approaches for tackling physical challenges, leveraging our recently introduced unified evaluation framework known as Learning Industrial Physical Simulations (LIPS). Building upon the preliminary edition held from November 2023 to March 2024, this iteration centers on a task fundamental to a well-established physical application: airfoil design simulation, utilizing our proposed AirfRANS dataset. The competition evaluates solutions based on various criteria encompassing ML accuracy, computational efficiency, Out-Of-Distribution performance, and adherence to physical principles. Notably, this competition represents a pioneering effort in exploring ML-driven surrogate methods aimed at optimizing the trade-off between computational efficiency and accuracy in physical simulations. Hosted on the Codabench platform, the competition offers online training and evaluation for all participating solutions.

AROMA: Preserving Spatial Structure for Latent PDE Modeling with Local Neural Fields

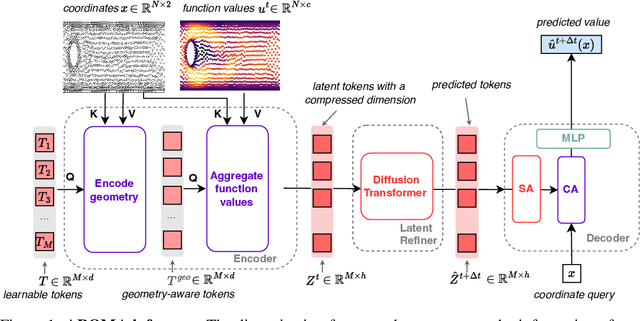
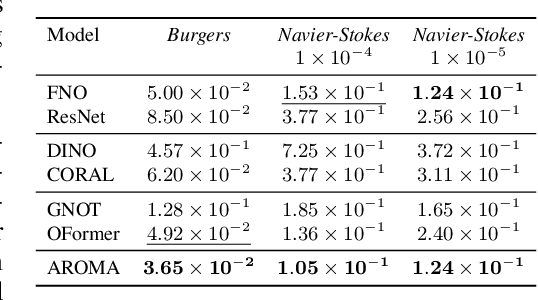
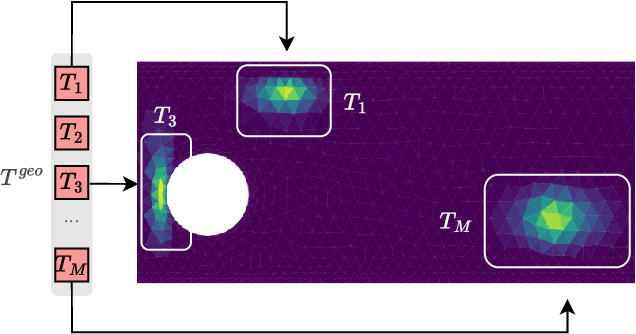
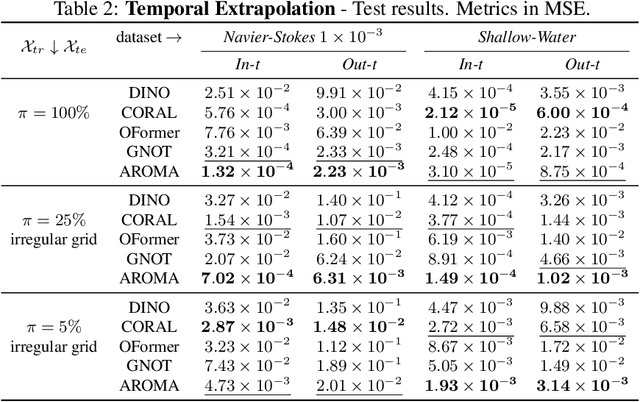
We present AROMA (Attentive Reduced Order Model with Attention), a framework designed to enhance the modeling of partial differential equations (PDEs) using local neural fields. Our flexible encoder-decoder architecture can obtain smooth latent representations of spatial physical fields from a variety of data types, including irregular-grid inputs and point clouds. This versatility eliminates the need for patching and allows efficient processing of diverse geometries. The sequential nature of our latent representation can be interpreted spatially and permits the use of a conditional transformer for modeling the temporal dynamics of PDEs. By employing a diffusion-based formulation, we achieve greater stability and enable longer rollouts compared to conventional MSE training. AROMA's superior performance in simulating 1D and 2D equations underscores the efficacy of our approach in capturing complex dynamical behaviors.