Probing Language Models on Their Knowledge Source

Large Language Models (LLMs) often encounter conflicts between their learned, internal (parametric knowledge, PK) and external knowledge provided during inference (contextual knowledge, CK). Understanding how LLMs models prioritize one knowledge source over the other remains a challenge. In this paper, we propose a novel probing framework to explore the mechanisms governing the selection between PK and CK in LLMs. Using controlled prompts designed to contradict the model's PK, we demonstrate that specific model activations are indicative of the knowledge source employed. We evaluate this framework on various LLMs of different sizes and demonstrate that mid-layer activations, particularly those related to relations in the input, are crucial in predicting knowledge source selection, paving the way for more reliable models capable of handling knowledge conflicts effectively.

Nonnegative matrix factorization with side information for time series recovery and prediction

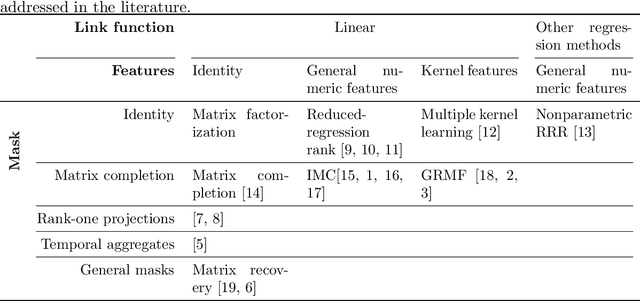
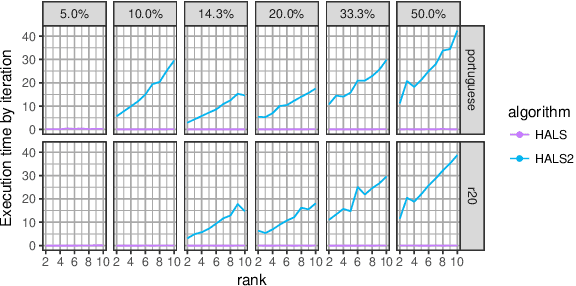
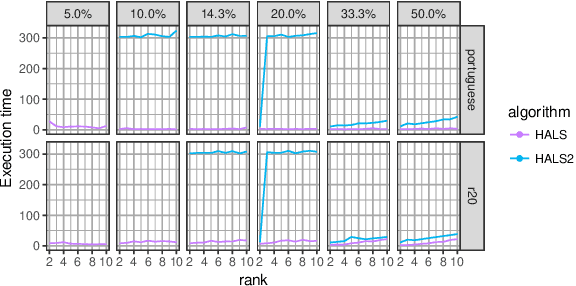
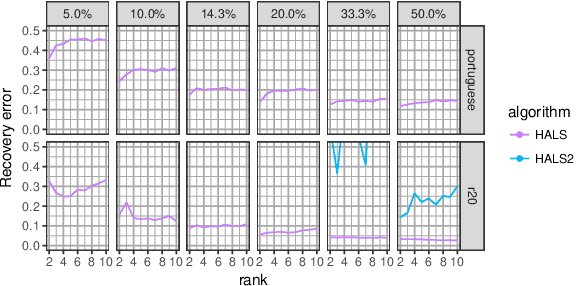
Motivated by the reconstruction and the prediction of electricity consumption, we extend Nonnegative Matrix Factorization~(NMF) to take into account side information (column or row features). We consider general linear measurement settings, and propose a framework which models non-linear relationships between features and the response variables. We extend previous theoretical results to obtain a sufficient condition on the identifiability of the NMF in this setting. Based the classical Hierarchical Alternating Least Squares~(HALS) algorithm, we propose a new algorithm (HALSX, or Hierarchical Alternating Least Squares with eXogeneous variables) which estimates the factorization model. The algorithm is validated on both simulated and real electricity consumption datasets as well as a recommendation dataset, to show its performance in matrix recovery and prediction for new rows and columns.

Recovering Multiple Nonnegative Time Series From a Few Temporal Aggregates

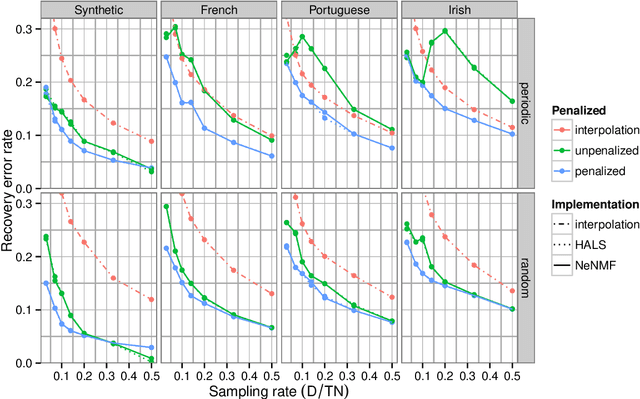
Motivated by electricity consumption metering, we extend existing nonnegative matrix factorization (NMF) algorithms to use linear measurements as observations, instead of matrix entries. The objective is to estimate multiple time series at a fine temporal scale from temporal aggregates measured on each individual series. Furthermore, our algorithm is extended to take into account individual autocorrelation to provide better estimation, using a recent convex relaxation of quadratically constrained quadratic program. Extensive experiments on synthetic and real-world electricity consumption datasets illustrate the effectiveness of our matrix recovery algorithms.