Node Regression on Latent Position Random Graphs via Local Averaging

Node regression consists in predicting the value of a graph label at a node, given observations at the other nodes. To gain some insight into the performance of various estimators for this task, we perform a theoretical study in a context where the graph is random. Specifically, we assume that the graph is generated by a Latent Position Model, where each node of the graph has a latent position, and the probability that two nodes are connected depend on the distance between the latent positions of the two nodes. In this context, we begin by studying the simplest possible estimator for graph regression, which consists in averaging the value of the label at all neighboring nodes. We show that in Latent Position Models this estimator tends to a Nadaraya Watson estimator in the latent space, and that its rate of convergence is in fact the same. One issue with this standard estimator is that it averages over a region consisting of all neighbors of a node, and that depending on the graph model this may be too much or too little. An alternative consists in first estimating the true distances between the latent positions, then injecting these estimated distances into a classical Nadaraya Watson estimator. This enables averaging in regions either smaller or larger than the typical graph neighborhood. We show that this method can achieve standard nonparametric rates in certain instances even when the graph neighborhood is too large or too small.

Generalization Bounds of Surrogate Policies for Combinatorial Optimization Problems

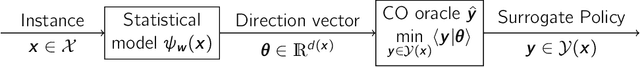
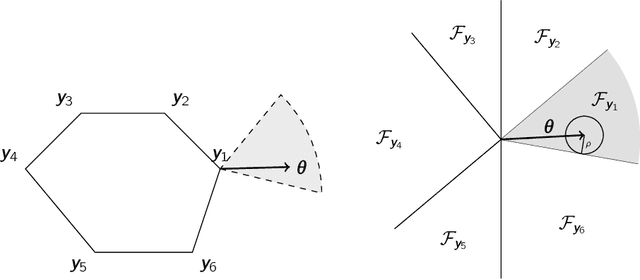
A recent stream of structured learning approaches has improved the practical state of the art for a range of combinatorial optimization problems with complex objectives encountered in operations research. Such approaches train policies that chain a statistical model with a surrogate combinatorial optimization oracle to map any instance of the problem to a feasible solution. The key idea is to exploit the statistical distribution over instances instead of dealing with instances separately. However learning such policies by risk minimization is challenging because the empirical risk is piecewise constant in the parameters, and few theoretical guarantees have been provided so far. In this article, we investigate methods that smooth the risk by perturbing the policy, which eases optimization and improves generalization. Our main contribution is a generalization bound that controls the perturbation bias, the statistical learning error, and the optimization error. Our analysis relies on the introduction of a uniform weak property, which captures and quantifies the interplay of the statistical model and the surrogate combinatorial optimization oracle. This property holds under mild assumptions on the statistical model, the surrogate optimization, and the instance data distribution. We illustrate the result on a range of applications such as stochastic vehicle scheduling. In particular, such policies are relevant for contextual stochastic optimization and our results cover this case.

FastPart: Over-Parameterized Stochastic Gradient Descent for Sparse optimisation on Measures

This paper presents a novel algorithm that leverages Stochastic Gradient Descent strategies in conjunction with Random Features to augment the scalability of Conic Particle Gradient Descent (CPGD) specifically tailored for solving sparse optimisation problems on measures. By formulating the CPGD steps within a variational framework, we provide rigorous mathematical proofs demonstrating the following key findings: (i) The total variation norms of the solution measures along the descent trajectory remain bounded, ensuring stability and preventing undesirable divergence; (ii) We establish a global convergence guarantee with a convergence rate of $\mathcal{O}(\log(K)/\sqrt{K})$ over $K$ iterations, showcasing the efficiency and effectiveness of our algorithm; (iii) Additionally, we analyze and establish local control over the first-order condition discrepancy, contributing to a deeper understanding of the algorithm's behavior and reliability in practical applications.

Exact recovery of the support of piecewise constant images via total variation regularization

This work is concerned with the recovery of piecewise constant images from noisy linear measurements. We study the noise robustness of a variational reconstruction method, which is based on total (gradient) variation regularization. We show that, if the unknown image is the superposition of a few simple shapes, and if a non-degenerate source condition holds, then, in the low noise regime, the reconstructed images have the same structure: they are the superposition of the same number of shapes, each a smooth deformation of one of the unknown shapes. Moreover, the reconstructed shapes and the associated intensities converge to the unknown ones as the noise goes to zero.

Three rates of convergence or separation via U-statistics in a dependent framework

Despite the ubiquity of U-statistics in modern Probability and Statistics, their non-asymptotic analysis in a dependent framework may have been overlooked. In a recent work, a new concentration inequality for U-statistics of order two for uniformly ergodic Markov chains has been proved. In this paper, we put this theoretical breakthrough into action by pushing further the current state of knowledge in three different active fields of research. First, we establish a new exponential inequality for the estimation of spectra of trace class integral operators with MCMC methods. The novelty is that this result holds for kernels with positive and negative eigenvalues, which is new as far as we know. In addition, we investigate generalization performance of online algorithms working with pairwise loss functions and Markov chain samples. We provide an online-to-batch conversion result by showing how we can extract a low risk hypothesis from the sequence of hypotheses generated by any online learner. We finally give a non-asymptotic analysis of a goodness-of-fit test on the density of the invariant measure of a Markov chain. We identify some classes of alternatives over which our test based on the $L_2$ distance has a prescribed power.

Latent Distance Estimation for Random Geometric Graphs

Random geometric graphs are a popular choice for a latent points generative model for networks. Their definition is based on a sample of $n$ points $X_1,X_2,\cdots,X_n$ on the Euclidean sphere~$\mathbb{S}^{d-1}$ which represents the latent positions of nodes of the network. The connection probabilities between the nodes are determined by an unknown function (referred to as the "link" function) evaluated at the distance between the latent points. We introduce a spectral estimator of the pairwise distance between latent points and we prove that its rate of convergence is the same as the nonparametric estimation of a function on $\mathbb{S}^{d-1}$, up to a logarithmic factor. In addition, we provide an efficient spectral algorithm to compute this estimator without any knowledge on the nonparametric link function. As a byproduct, our method can also consistently estimate the dimension $d$ of the latent space.

Sparse Recovery Guarantees from Extreme Eigenvalues Small Deviations

This article provides a new toolbox to derive sparse recovery guarantees from small deviations on extreme singular values or extreme eigenvalues obtained in Random Matrix Theory. This work is based on Restricted Isometry Constants (RICs) which are a pivotal notion in Compressed Sensing and High-Dimensional Statistics as these constants finely assess how a linear operator is conditioned on the set of sparse vectors and hence how it performs in SRSR. While it is an open problem to construct deterministic matrices with apposite RICs, one can prove that such matrices exist using random matrices models. In this paper, we show upper bounds on RICs for Gaussian and Rademacher matrices using state-of-the-art small deviation estimates on their extreme eigenvalues. This allows us to derive a lower bound on the probability of getting SRSR. One benefit of this paper is a direct and explicit derivation of upper bounds on RICs and lower bounds on SRSR from small deviations on the extreme eigenvalues given by Random Matrix theory.

Nonnegative matrix factorization with side information for time series recovery and prediction

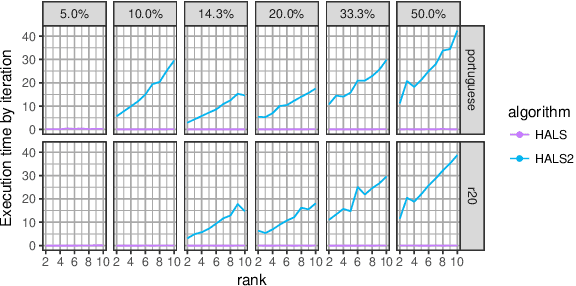
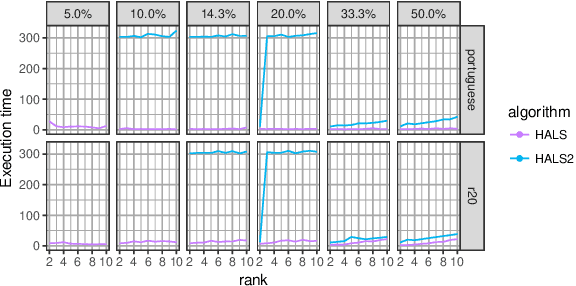
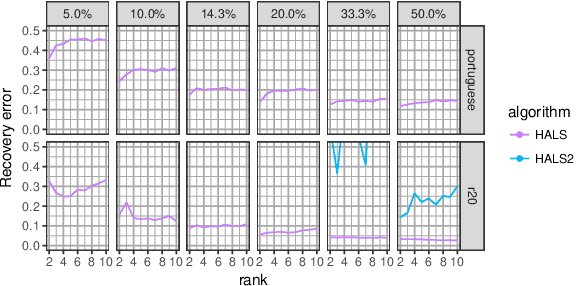
Motivated by the reconstruction and the prediction of electricity consumption, we extend Nonnegative Matrix Factorization~(NMF) to take into account side information (column or row features). We consider general linear measurement settings, and propose a framework which models non-linear relationships between features and the response variables. We extend previous theoretical results to obtain a sufficient condition on the identifiability of the NMF in this setting. Based the classical Hierarchical Alternating Least Squares~(HALS) algorithm, we propose a new algorithm (HALSX, or Hierarchical Alternating Least Squares with eXogeneous variables) which estimates the factorization model. The algorithm is validated on both simulated and real electricity consumption datasets as well as a recommendation dataset, to show its performance in matrix recovery and prediction for new rows and columns.

Reconstructing undirected graphs from eigenspaces

In this paper, we aim at recovering an undirected weighted graph of $N$ vertices from the knowledge of a perturbed version of the eigenspaces of its adjacency matrix $W$. For instance, this situation arises for stationary signals on graphs or for Markov chains observed at random times. Our approach is based on minimizing a cost function given by the Frobenius norm of the commutator $\mathsf{A} \mathsf{B}-\mathsf{B} \mathsf{A}$ between symmetric matrices $\mathsf{A}$ and $\mathsf{B}$. In the Erd\H{o}s-R\'enyi model with no self-loops, we show that identifiability (i.e., the ability to reconstruct $W$ from the knowledge of its eigenspaces) follows a sharp phase transition on the expected number of edges with threshold function $N\log N/2$. Given an estimation of the eigenspaces based on a $n$-sample, we provide support selection procedures from theoretical and practical point of views. In particular, when deleting an edge from the active support, our study unveils that our test statistic is the order of $\mathcal O(1/n)$ when we overestimate the true support and lower bounded by a positive constant when the estimated support is smaller than the true support. This feature leads to a powerful practical support estimation procedure. Simulated and real life numerical experiments assert our new methodology.

Recovering Multiple Nonnegative Time Series From a Few Temporal Aggregates

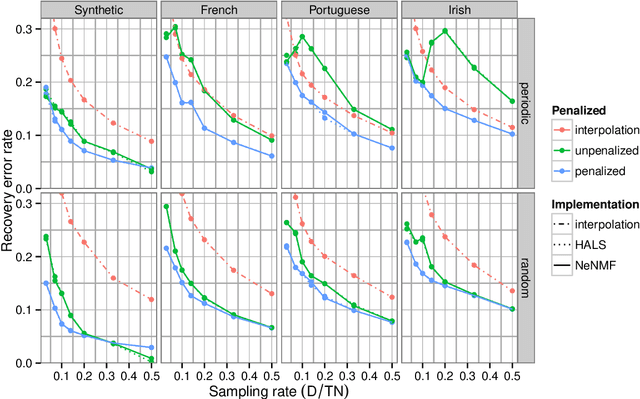
Motivated by electricity consumption metering, we extend existing nonnegative matrix factorization (NMF) algorithms to use linear measurements as observations, instead of matrix entries. The objective is to estimate multiple time series at a fine temporal scale from temporal aggregates measured on each individual series. Furthermore, our algorithm is extended to take into account individual autocorrelation to provide better estimation, using a recent convex relaxation of quadratically constrained quadratic program. Extensive experiments on synthetic and real-world electricity consumption datasets illustrate the effectiveness of our matrix recovery algorithms.