Nonnegative matrix factorization with side information for time series recovery and prediction
Paper and Code
Sep 19, 2017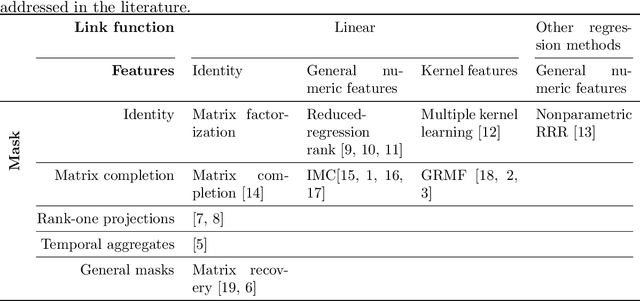
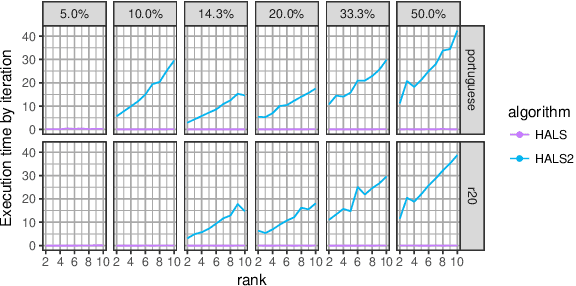
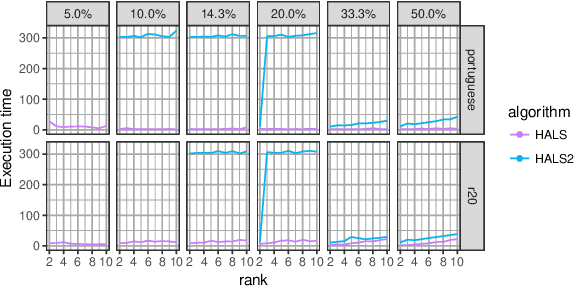
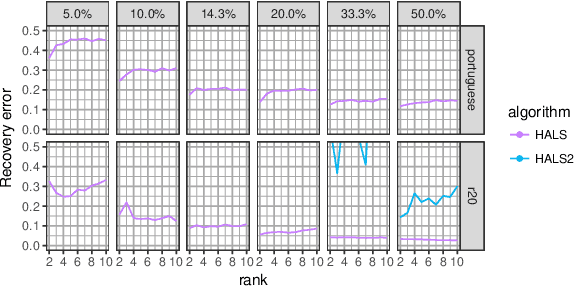
Motivated by the reconstruction and the prediction of electricity consumption, we extend Nonnegative Matrix Factorization~(NMF) to take into account side information (column or row features). We consider general linear measurement settings, and propose a framework which models non-linear relationships between features and the response variables. We extend previous theoretical results to obtain a sufficient condition on the identifiability of the NMF in this setting. Based the classical Hierarchical Alternating Least Squares~(HALS) algorithm, we propose a new algorithm (HALSX, or Hierarchical Alternating Least Squares with eXogeneous variables) which estimates the factorization model. The algorithm is validated on both simulated and real electricity consumption datasets as well as a recommendation dataset, to show its performance in matrix recovery and prediction for new rows and columns.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge