Open challenges for Machine Learning based Early Decision-Making research

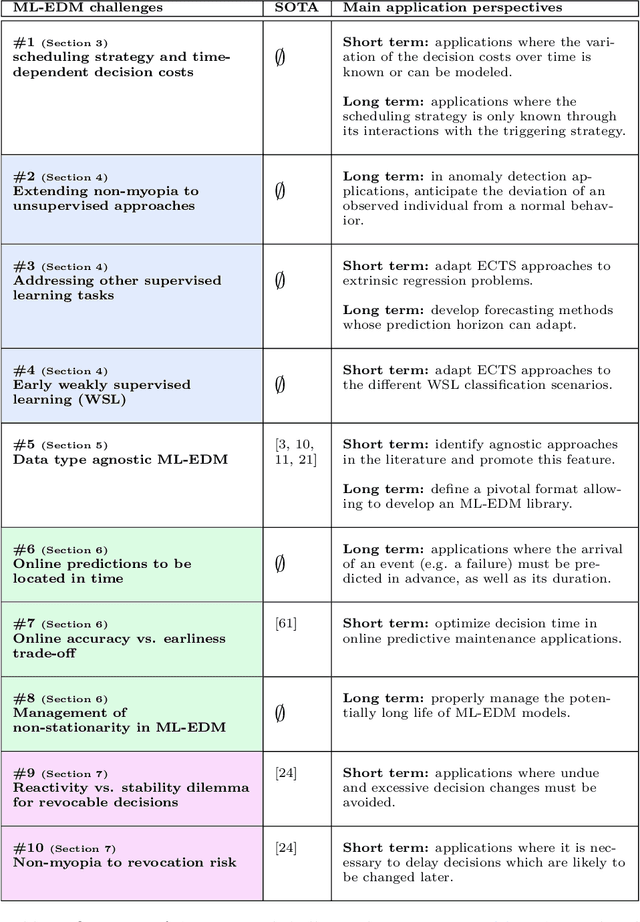
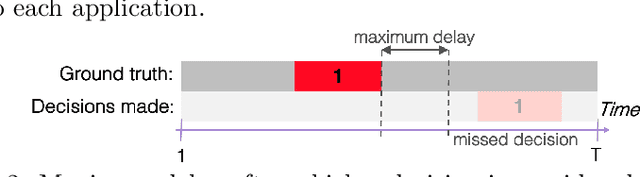
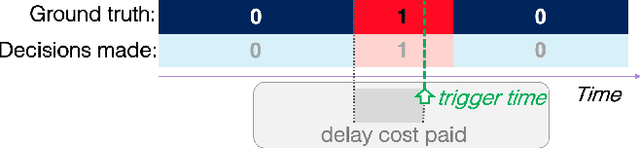
More and more applications require early decisions, i.e. taken as soon as possible from partially observed data. However, the later a decision is made, the more its accuracy tends to improve, since the description of the problem to hand is enriched over time. Such a compromise between the earliness and the accuracy of decisions has been particularly studied in the field of Early Time Series Classification. This paper introduces a more general problem, called Machine Learning based Early Decision Making (ML-EDM), which consists in optimizing the decision times of models in a wide range of settings where data is collected over time. After defining the ML-EDM problem, ten challenges are identified and proposed to the scientific community to further research in this area. These challenges open important application perspectives, discussed in this paper.

Autoencoder-based time series clustering with energy applications

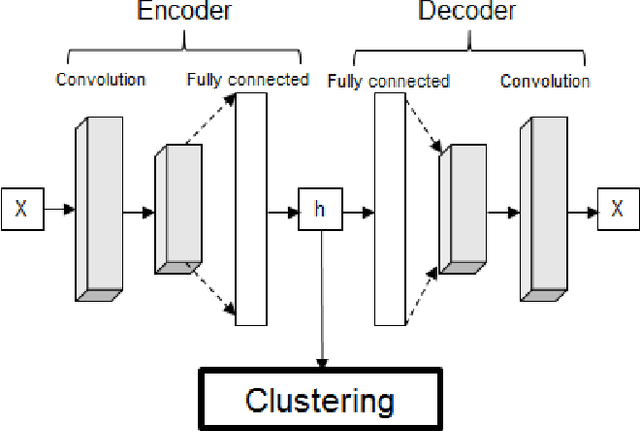
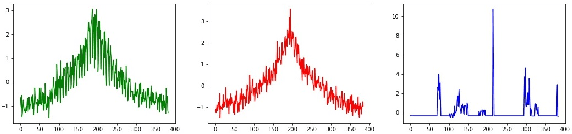
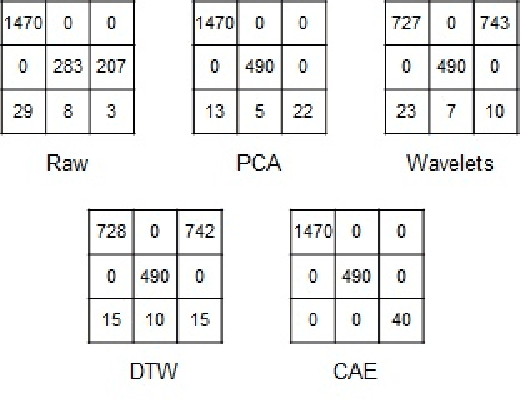
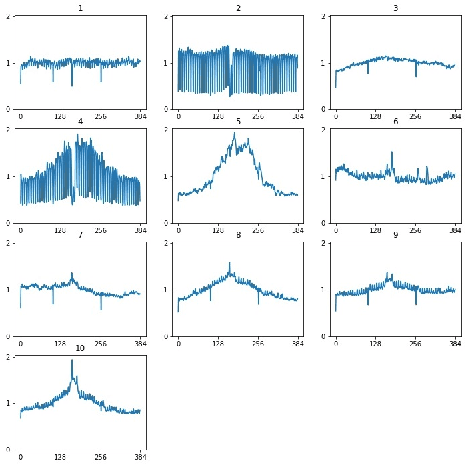
Time series clustering is a challenging task due to the specific nature of the data. Classical approaches do not perform well and need to be adapted either through a new distance measure or a data transformation. In this paper we investigate the combination of a convolutional autoencoder and a k-medoids algorithm to perfom time series clustering. The convolutional autoencoder allows to extract meaningful features and reduce the dimension of the data, leading to an improvement of the subsequent clustering. Using simulation and energy related data to validate the approach, experimental results show that the clustering is robust to outliers thus leading to finer clusters than with standard methods.

Nonnegative matrix factorization with side information for time series recovery and prediction

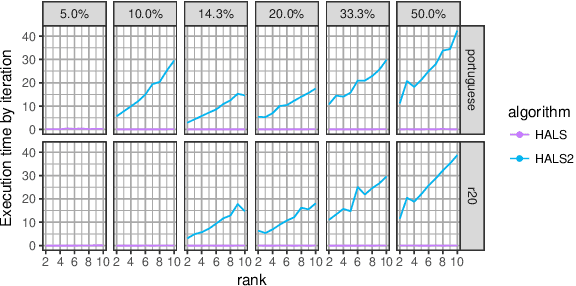
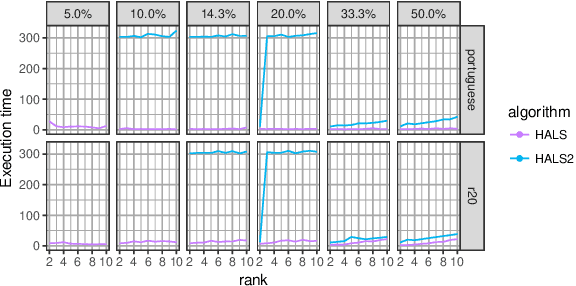
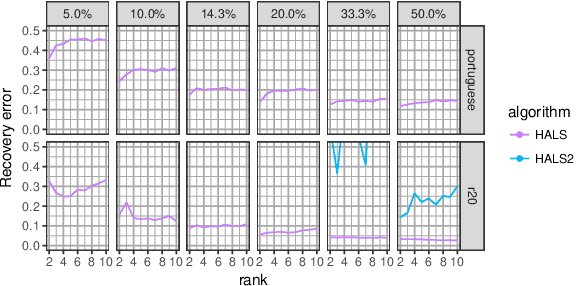
Motivated by the reconstruction and the prediction of electricity consumption, we extend Nonnegative Matrix Factorization~(NMF) to take into account side information (column or row features). We consider general linear measurement settings, and propose a framework which models non-linear relationships between features and the response variables. We extend previous theoretical results to obtain a sufficient condition on the identifiability of the NMF in this setting. Based the classical Hierarchical Alternating Least Squares~(HALS) algorithm, we propose a new algorithm (HALSX, or Hierarchical Alternating Least Squares with eXogeneous variables) which estimates the factorization model. The algorithm is validated on both simulated and real electricity consumption datasets as well as a recommendation dataset, to show its performance in matrix recovery and prediction for new rows and columns.

Recovering Multiple Nonnegative Time Series From a Few Temporal Aggregates

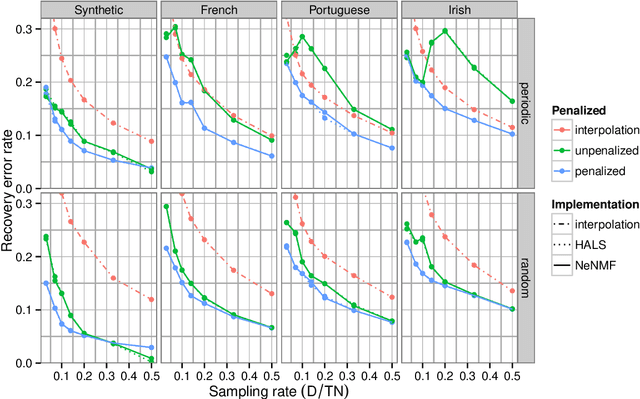
Motivated by electricity consumption metering, we extend existing nonnegative matrix factorization (NMF) algorithms to use linear measurements as observations, instead of matrix entries. The objective is to estimate multiple time series at a fine temporal scale from temporal aggregates measured on each individual series. Furthermore, our algorithm is extended to take into account individual autocorrelation to provide better estimation, using a recent convex relaxation of quadratically constrained quadratic program. Extensive experiments on synthetic and real-world electricity consumption datasets illustrate the effectiveness of our matrix recovery algorithms.

Exploratory Analysis of Functional Data via Clustering and Optimal Segmentation

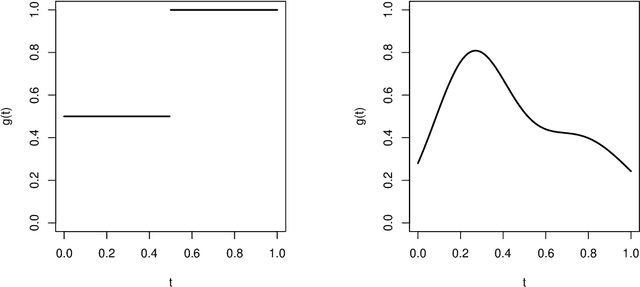
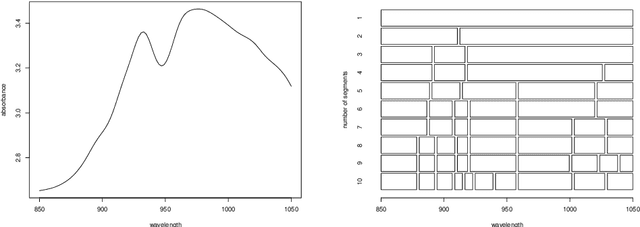
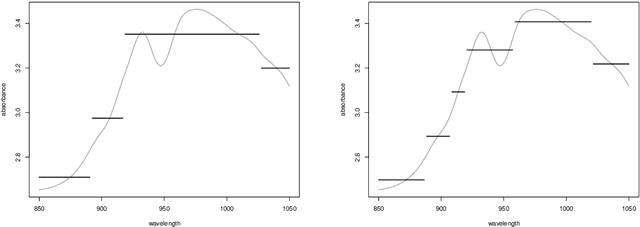
We propose in this paper an exploratory analysis algorithm for functional data. The method partitions a set of functions into $K$ clusters and represents each cluster by a simple prototype (e.g., piecewise constant). The total number of segments in the prototypes, $P$, is chosen by the user and optimally distributed among the clusters via two dynamic programming algorithms. The practical relevance of the method is shown on two real world datasets.