Node Regression on Latent Position Random Graphs via Local Averaging

Node regression consists in predicting the value of a graph label at a node, given observations at the other nodes. To gain some insight into the performance of various estimators for this task, we perform a theoretical study in a context where the graph is random. Specifically, we assume that the graph is generated by a Latent Position Model, where each node of the graph has a latent position, and the probability that two nodes are connected depend on the distance between the latent positions of the two nodes. In this context, we begin by studying the simplest possible estimator for graph regression, which consists in averaging the value of the label at all neighboring nodes. We show that in Latent Position Models this estimator tends to a Nadaraya Watson estimator in the latent space, and that its rate of convergence is in fact the same. One issue with this standard estimator is that it averages over a region consisting of all neighbors of a node, and that depending on the graph model this may be too much or too little. An alternative consists in first estimating the true distances between the latent positions, then injecting these estimated distances into a classical Nadaraya Watson estimator. This enables averaging in regions either smaller or larger than the typical graph neighborhood. We show that this method can achieve standard nonparametric rates in certain instances even when the graph neighborhood is too large or too small.

A Faster Sampler for Discrete Determinantal Point Processes

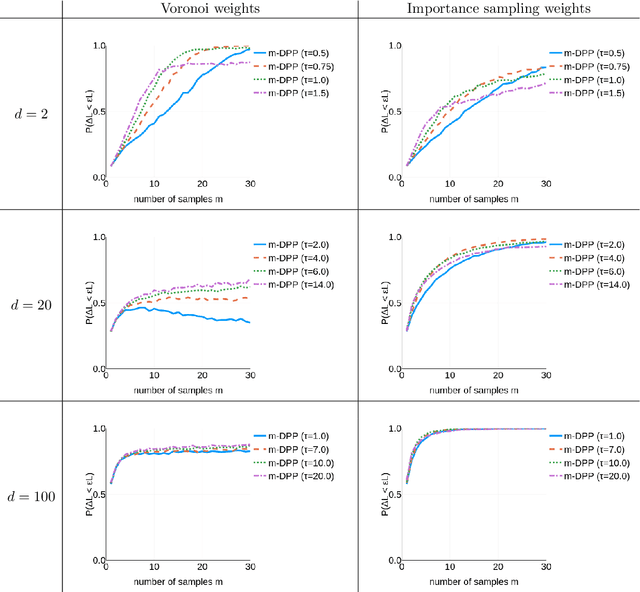
Discrete Determinantal Point Processes (DPPs) have a wide array of potential applications for subsampling datasets. They are however held back in some cases by the high cost of sampling. In the worst-case scenario, the sampling cost scales as $O(n^3)$ where n is the number of elements of the ground set. A popular workaround to this prohibitive cost is to sample DPPs defined by low-rank kernels. In such cases, the cost of standard sampling algorithms scales as $O(np^2 + nm^2)$ where m is the (average) number of samples of the DPP (usually $m \ll n$) and p ($m \leq p \leq n$) the rank of the kernel used to define the DPP. The first term, $O(np^2)$, comes from a SVD-like step. We focus here on the second term of this cost, $O(nm^2)$, and show that it can be brought down to $O(nm + m^3 log m)$ without loss on the sampling's exactness. In practice, we observe extremely substantial speedups compared to the classical algorithm as soon as $n > 1, 000$. The algorithm described here is a close variant of the standard algorithm for sampling continuous DPPs, and uses rejection sampling. In the specific case of projection DPPs, we also show that any additional sample can be drawn in time $O(m^3 log m)$. Finally, an interesting by-product of the analysis is that a realisation from a DPP is typically contained in a subset of size $O(m log m)$ formed using leverage score i.i.d. sampling.

Variance reduction in stochastic methods for large-scale regularised least-squares problems

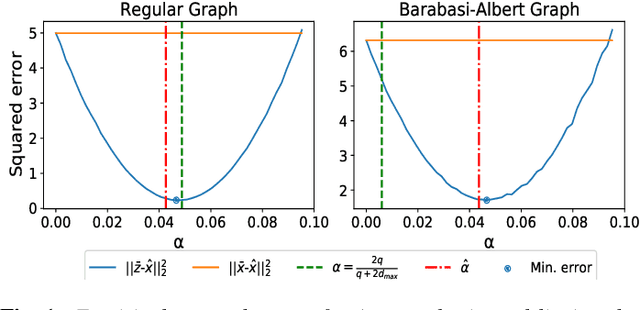
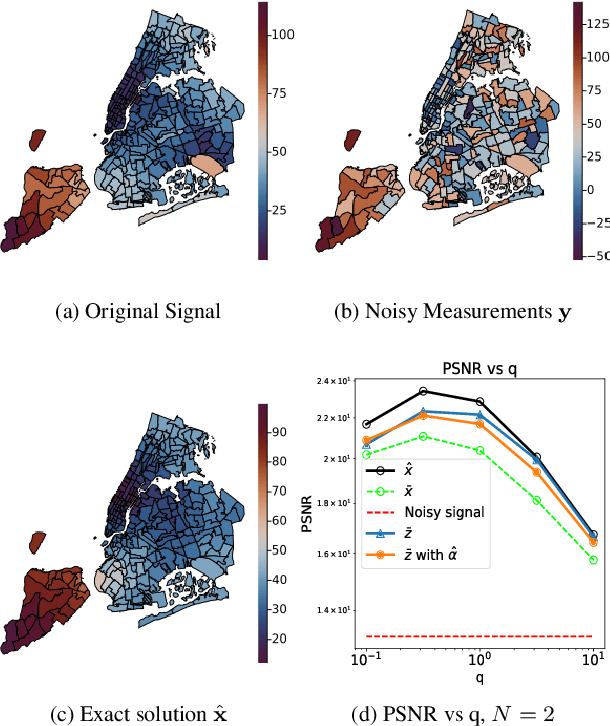
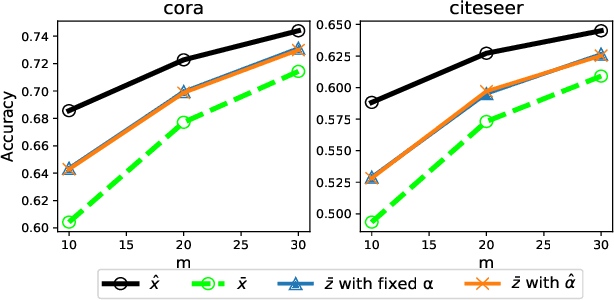
Large dimensional least-squares and regularised least-squares problems are expensive to solve. There exist many approximate techniques, some deterministic (like conjugate gradient), some stochastic (like stochastic gradient descent). Among the latter, a new class of techniques uses Determinantal Point Processes (DPPs) to produce unbiased estimators of the solution. In particular, they can be used to perform Tikhonov regularization on graphs using random spanning forests, a specific DPP. While the unbiasedness of these algorithms is attractive, their variance can be high. We show here that variance can be reduced by combining the stochastic estimator with a deterministic gradient-descent step, while keeping the property of unbiasedness. We apply this technique to Tikhonov regularization on graphs, where the reduction in variance is found to be substantial at very small extra cost.

Asymptotic Equivalence of Fixed-size and Varying-size Determinantal Point Processes

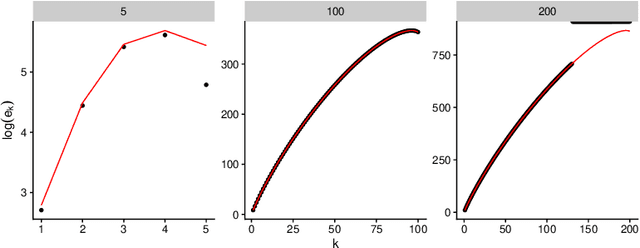
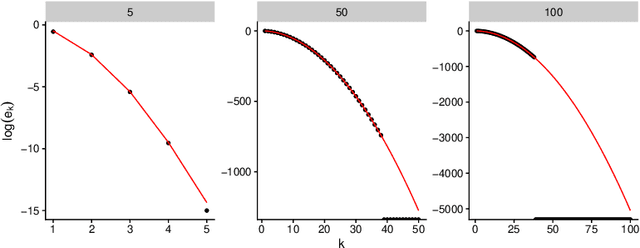
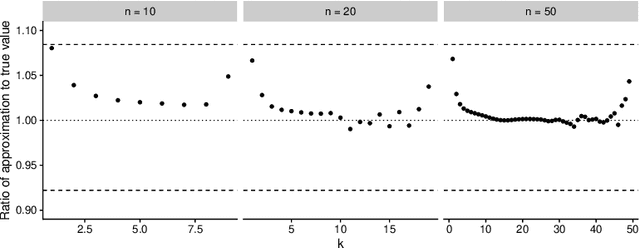
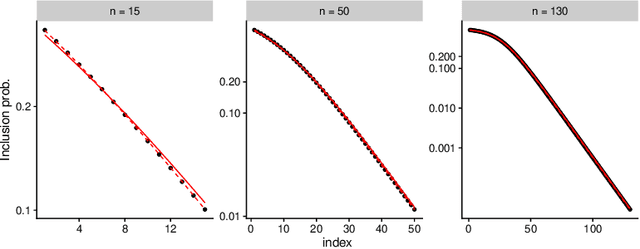
Determinantal Point Processes (DPPs) are popular models for point processes with repulsion. They appear in numerous contexts, from physics to graph theory, and display appealing theoretical properties. On the more practical side of things, since DPPs tend to select sets of points that are some distance apart (repulsion), they have been advocated as a way of producing random subsets with high diversity. DPPs come in two variants: fixed-size and varying-size. A sample from a varying-size DPP is a subset of random cardinality, while in fixed-size "$k$-DPPs" the cardinality is fixed. The latter makes more sense in many applications, but unfortunately their computational properties are less attractive, since, among other things, inclusion probabilities are harder to compute. In this work we show that as the size of the ground set grows, $k$-DPPs and DPPs become equivalent, meaning that their inclusion probabilities converge. As a by-product, we obtain saddlepoint formulas for inclusion probabilities in $k$-DPPs. These turn out to be extremely accurate, and suffer less from numerical difficulties than exact methods do. Our results also suggest that $k$-DPPs and DPPs also have equivalent maximum likelihood estimators. Finally, we obtain results on asymptotic approximations of elementary symmetric polynomials which may be of independent interest.

Determinantal Point Processes for Coresets

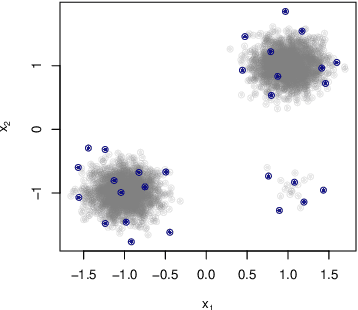
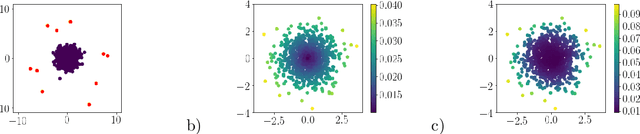
When one is faced with a dataset too large to be used all at once, an obvious solution is to retain only part of it. In practice this takes a wide variety of different forms, but among them "coresets" are especially appealing. A coreset is a (small) weighted sample of the original data that comes with a guarantee: that a cost function can be evaluated on the smaller set instead of the larger one, with low relative error. For some classes of problems, and via a careful choice of sampling distribution, iid random sampling has turned to be one of the most successful methods to build coresets efficiently. However, independent samples are sometimes overly redundant, and one could hope that enforcing diversity would lead to better performance. The difficulty lies in proving coreset properties in non-iid samples. We show that the coreset property holds for samples formed with determinantal point processes (DPP). DPPs are interesting because they are a rare example of repulsive point processes with tractable theoretical properties, enabling us to construct general coreset theorems. We apply our results to the $k$-means problem, and give empirical evidence of the superior performance of DPP samples over state of the art methods.

Graph sampling with determinantal processes

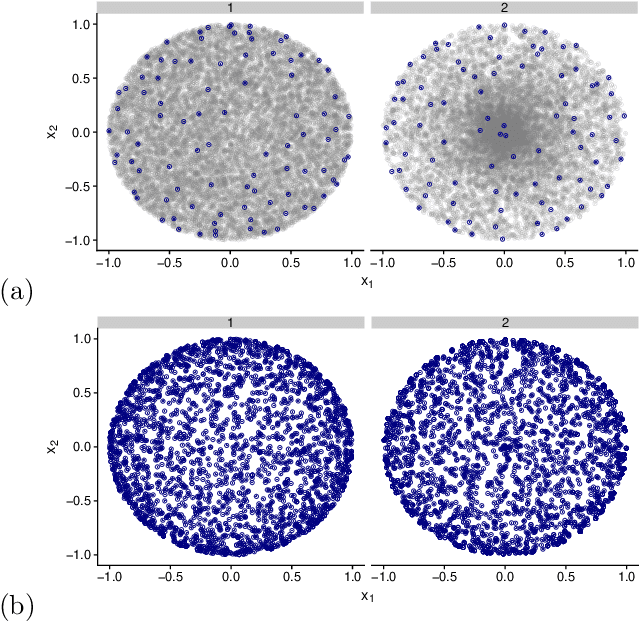
We present a new random sampling strategy for k-bandlimited signals defined on graphs, based on determinantal point processes (DPP). For small graphs, ie, in cases where the spectrum of the graph is accessible, we exhibit a DPP sampling scheme that enables perfect recovery of bandlimited signals. For large graphs, ie, in cases where the graph's spectrum is not accessible, we investigate, both theoretically and empirically, a sub-optimal but much faster DPP based on loop-erased random walks on the graph. Preliminary experiments show promising results especially in cases where the number of measurements should stay as small as possible and for graphs that have a strong community structure. Our sampling scheme is efficient and can be applied to graphs with up to $10^6$ nodes.

The Poisson transform for unnormalised statistical models

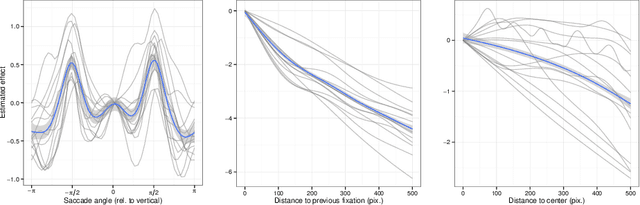
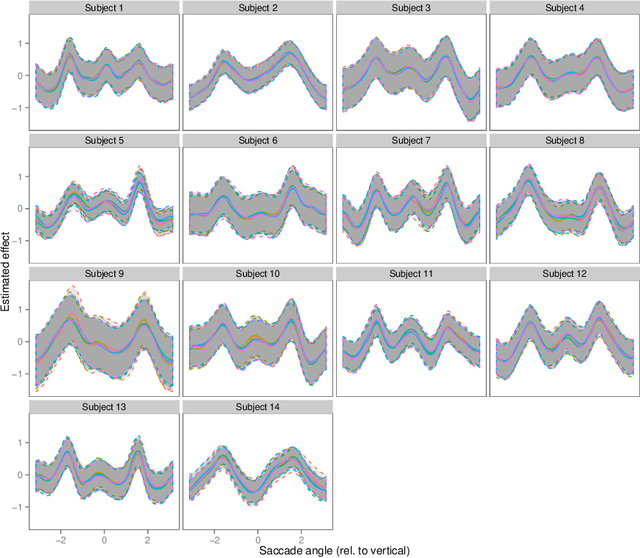
Contrary to standard statistical models, unnormalised statistical models only specify the likelihood function up to a constant. While such models are natural and popular, the lack of normalisation makes inference much more difficult. Here we show that inferring the parameters of a unnormalised model on a space $\Omega$ can be mapped onto an equivalent problem of estimating the intensity of a Poisson point process on $\Omega$. The unnormalised statistical model now specifies an intensity function that does not need to be normalised. Effectively, the normalisation constant may now be inferred as just another parameter, at no loss of information. The result can be extended to cover non-IID models, which includes for example unnormalised models for sequences of graphs (dynamical graphs), or for sequences of binary vectors. As a consequence, we prove that unnormalised parameteric inference in non-IID models can be turned into a semi-parametric estimation problem. Moreover, we show that the noise-contrastive divergence of Gutmann & Hyv\"arinen (2012) can be understood as an approximation of the Poisson transform, and extended to non-IID settings. We use our results to fit spatial Markov chain models of eye movements, where the Poisson transform allows us to turn a highly non-standard model into vanilla semi-parametric logistic regression.

Expectation-Propagation for Likelihood-Free Inference

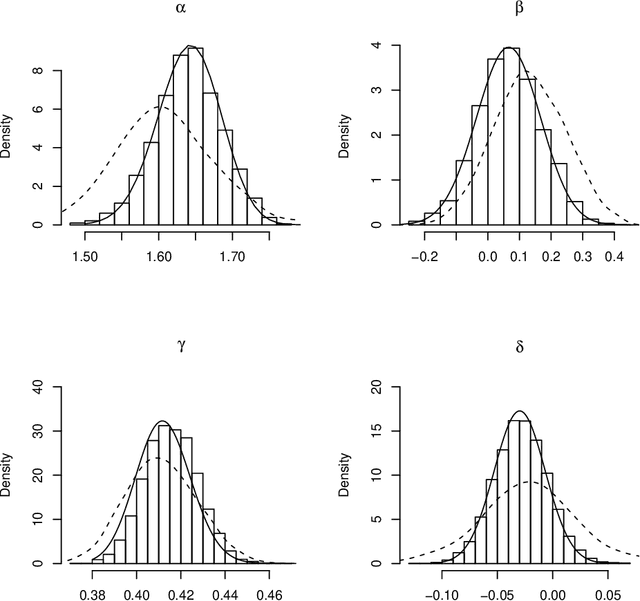
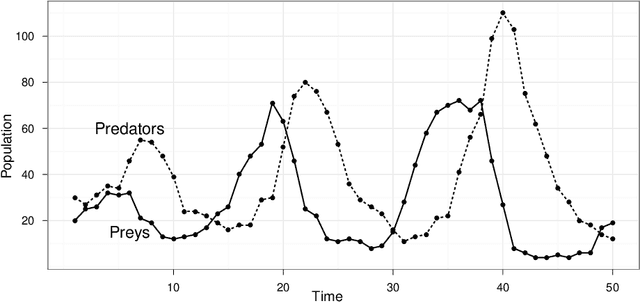
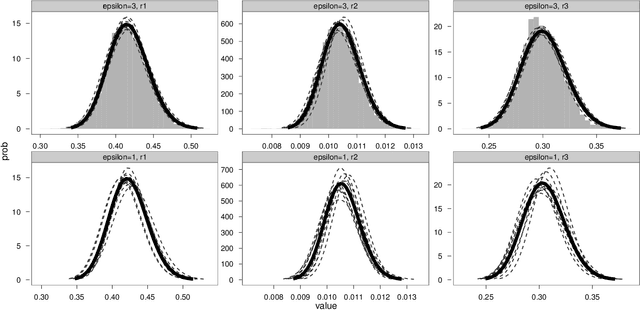
Many models of interest in the natural and social sciences have no closed-form likelihood function, which means that they cannot be treated using the usual techniques of statistical inference. In the case where such models can be efficiently simulated, Bayesian inference is still possible thanks to the Approximate Bayesian Computation (ABC) algorithm. Although many refinements have been suggested, ABC inference is still far from routine. ABC is often excruciatingly slow due to very low acceptance rates. In addition, ABC requires introducing a vector of "summary statistics", the choice of which is relatively arbitrary, and often require some trial and error, making the whole process quite laborious for the user. We introduce in this work the EP-ABC algorithm, which is an adaptation to the likelihood-free context of the variational approximation algorithm known as Expectation Propagation (Minka, 2001). The main advantage of EP-ABC is that it is faster by a few orders of magnitude than standard algorithms, while producing an overall approximation error which is typically negligible. A second advantage of EP-ABC is that it replaces the usual global ABC constraint on the vector of summary statistics computed on the whole dataset, by n local constraints of the form that apply separately to each data-point. As a consequence, it is often possible to do away with summary statistics entirely. In that case, EP-ABC approximates directly the evidence (marginal likelihood) of the model. Comparisons are performed in three real-world applications which are typical of likelihood-free inference, including one application in neuroscience which is novel, and possibly too challenging for standard ABC techniques.