Split Covariance Intersection with Correlated Components for Distributed Estimation

This paper introduces a new conservative fusion method to exploit the correlated components within the estimation errors. Fusion is the process of combining multiple estimates of a given state to produce a new estimate with a smaller MSE. To perform the optimal linear fusion, the (centralized) covariance associated with the errors of all estimates is required. If it is partially unknown, the optimal fusion cannot be computed. Instead, a solution is to perform a conservative fusion. A conservative fusion provides a gain and a bound on the resulting MSE matrix which guarantees that the error is not underestimated. A well-known conservative fusion is the Covariance Intersection fusion. It has been modified to exploit the uncorrelated components within the errors. In this paper, it is further extended to exploit the correlated components as well. The resulting fusion is integrated into standard distributed algorithms where it allows exploiting the process noise observed by all agents. The improvement is confirmed by simulations.

Pseudorange Rigidity and Solvability of Cooperative GNSS Positioning

Global Navigation Satellite Systems (GNSS) are a widely used technology for positioning and navigation. GNSS positioning relies on pseudorange measurements from satellites to receivers. A pseudorange is the apparent distance between two agents deduced from the time-of-flight of a signal sent from one agent to the other. Because of the lack of synchronization between the agents' clocks, it is a biased version of their distance. This paper introduces a new rigidity theory adapted to pseudorange measurements. The peculiarity of pseudoranges is that they are asymmetrical measurements. Therefore, unlike other usual rigidities, the graphs of pseudorange frameworks are directed. In this paper, pseudorange rigidity is proved to be a generic property of the underlying undirected graph of constraints. The main result is a characterization of rigid pseudorange graphs as combinations of rigid distance graphs and connected graphs. This new theory is adapted for GNSS. It provides new insights into the minimum number of satellites needed to locate a receiver, and is applied to the localization of GNSS cooperative networks of receivers. The interests of asymmetrical constraints in the context of formation control are also discussed.

Fusion of Distance Measurements between Agents with Unknown Correlations

Cooperative localization is a promising solution to improve the accuracy and overcome the shortcomings of GNSS. Cooperation is often achieved by measuring the distance between users. To optimally integrate a distance measurement between two users into a navigation filter, the correlation between the errors of their estimates must be known. Unfortunately, in large scale networks the agents cannot compute these correlations and must use consistent filters. A consistent filter provides an upper bound on the covariance of the error of the estimator taking into account all the possible correlations. In this paper, a consistent linear filter for integrating a distance measurement is derived using Split Covariance Intersection. Its analysis shows that a distance measurement between two agents can only benefit one of them, i.e., only one of the two can use the distance measurement to improve its estimator. Furthermore, in some cases, none can. A necessary condition for an agent to benefit from the measurement is given for a general class of objective functions. When the objective function is the trace or the determinant, necessary and sufficient conditions are given.

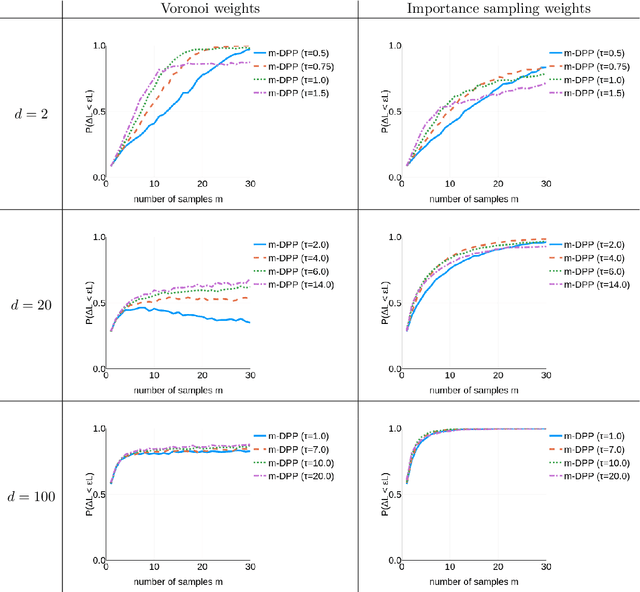
A Faster Sampler for Discrete Determinantal Point Processes

Discrete Determinantal Point Processes (DPPs) have a wide array of potential applications for subsampling datasets. They are however held back in some cases by the high cost of sampling. In the worst-case scenario, the sampling cost scales as $O(n^3)$ where n is the number of elements of the ground set. A popular workaround to this prohibitive cost is to sample DPPs defined by low-rank kernels. In such cases, the cost of standard sampling algorithms scales as $O(np^2 + nm^2)$ where m is the (average) number of samples of the DPP (usually $m \ll n$) and p ($m \leq p \leq n$) the rank of the kernel used to define the DPP. The first term, $O(np^2)$, comes from a SVD-like step. We focus here on the second term of this cost, $O(nm^2)$, and show that it can be brought down to $O(nm + m^3 log m)$ without loss on the sampling's exactness. In practice, we observe extremely substantial speedups compared to the classical algorithm as soon as $n > 1, 000$. The algorithm described here is a close variant of the standard algorithm for sampling continuous DPPs, and uses rejection sampling. In the specific case of projection DPPs, we also show that any additional sample can be drawn in time $O(m^3 log m)$. Finally, an interesting by-product of the analysis is that a realisation from a DPP is typically contained in a subset of size $O(m log m)$ formed using leverage score i.i.d. sampling.

Variance Reduction for Inverse Trace Estimation via Random Spanning Forests

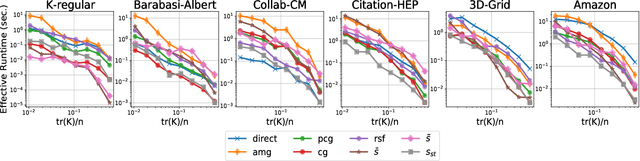
The trace $\tr(q(\ma{L} + q\ma{I})^{-1})$, where $\ma{L}$ is a symmetric diagonally dominant matrix, is the quantity of interest in some machine learning problems. However, its direct computation is impractical if the matrix size is large. State-of-the-art methods include Hutchinson's estimator combined with iterative solvers, as well as the estimator based on random spanning forests (a random process on graphs). In this work, we show two ways of improving the forest-based estimator via well-known variance reduction techniques, namely control variates and stratified sampling. Implementing these techniques is easy, and provides substantial variance reduction, yielding comparable or better performance relative to state-of-the-art algorithms.

Variance reduction in stochastic methods for large-scale regularised least-squares problems

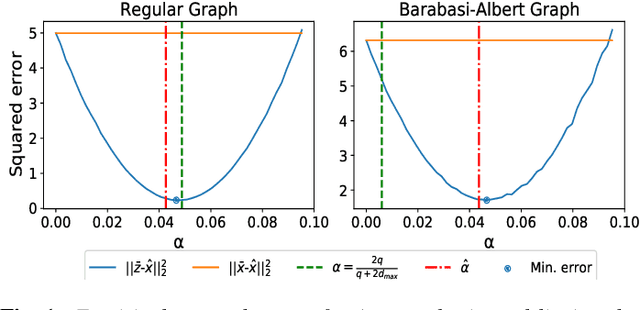
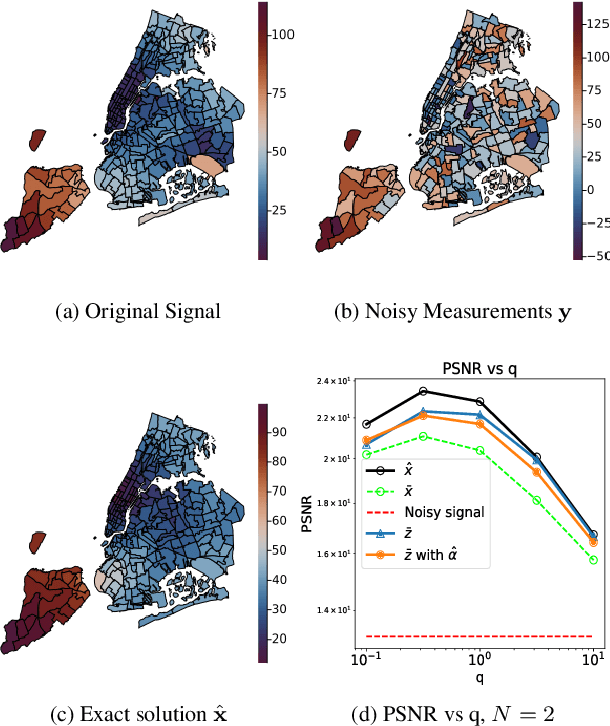
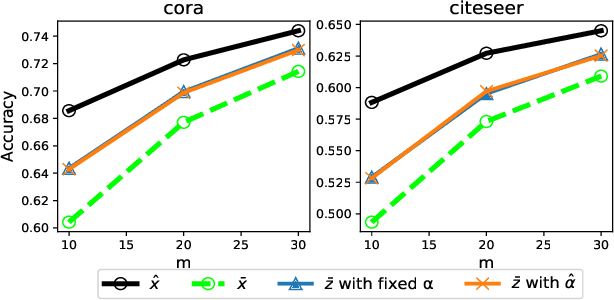
Large dimensional least-squares and regularised least-squares problems are expensive to solve. There exist many approximate techniques, some deterministic (like conjugate gradient), some stochastic (like stochastic gradient descent). Among the latter, a new class of techniques uses Determinantal Point Processes (DPPs) to produce unbiased estimators of the solution. In particular, they can be used to perform Tikhonov regularization on graphs using random spanning forests, a specific DPP. While the unbiasedness of these algorithms is attractive, their variance can be high. We show here that variance can be reduced by combining the stochastic estimator with a deterministic gradient-descent step, while keeping the property of unbiasedness. We apply this technique to Tikhonov regularization on graphs, where the reduction in variance is found to be substantial at very small extra cost.

Asymptotic Equivalence of Fixed-size and Varying-size Determinantal Point Processes

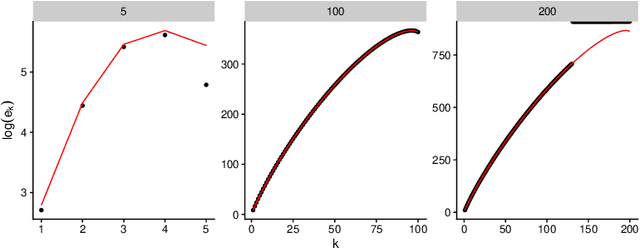
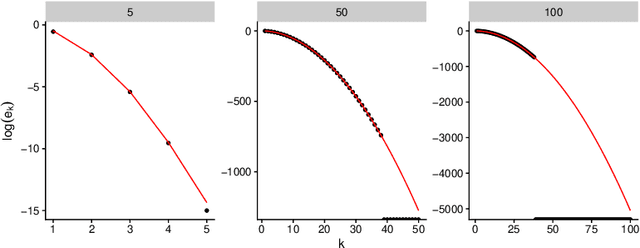
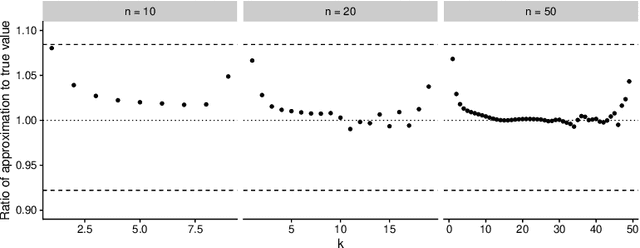
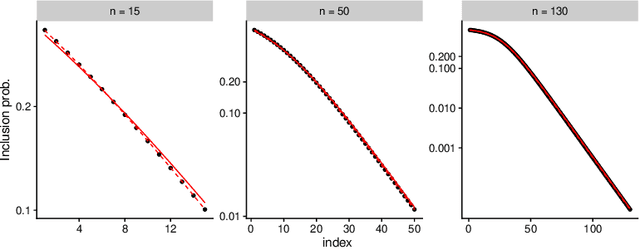
Determinantal Point Processes (DPPs) are popular models for point processes with repulsion. They appear in numerous contexts, from physics to graph theory, and display appealing theoretical properties. On the more practical side of things, since DPPs tend to select sets of points that are some distance apart (repulsion), they have been advocated as a way of producing random subsets with high diversity. DPPs come in two variants: fixed-size and varying-size. A sample from a varying-size DPP is a subset of random cardinality, while in fixed-size "$k$-DPPs" the cardinality is fixed. The latter makes more sense in many applications, but unfortunately their computational properties are less attractive, since, among other things, inclusion probabilities are harder to compute. In this work we show that as the size of the ground set grows, $k$-DPPs and DPPs become equivalent, meaning that their inclusion probabilities converge. As a by-product, we obtain saddlepoint formulas for inclusion probabilities in $k$-DPPs. These turn out to be extremely accurate, and suffer less from numerical difficulties than exact methods do. Our results also suggest that $k$-DPPs and DPPs also have equivalent maximum likelihood estimators. Finally, we obtain results on asymptotic approximations of elementary symmetric polynomials which may be of independent interest.

Determinantal Point Processes for Coresets

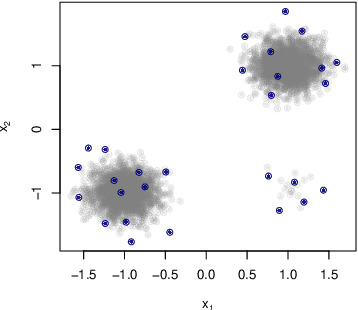
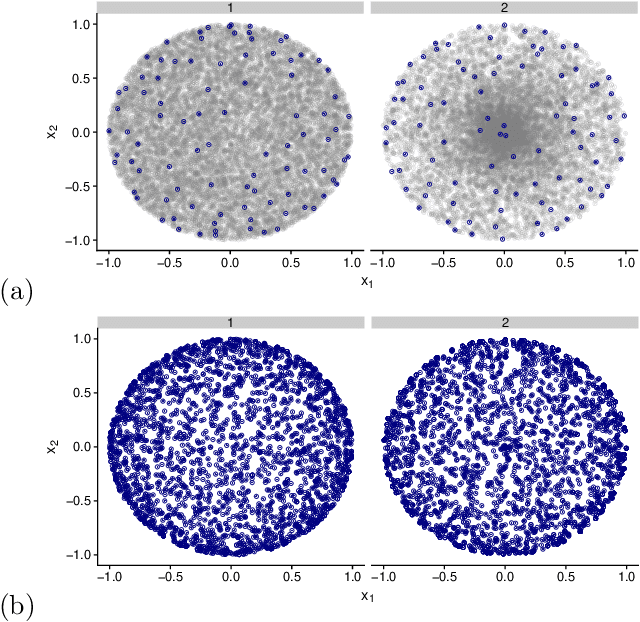
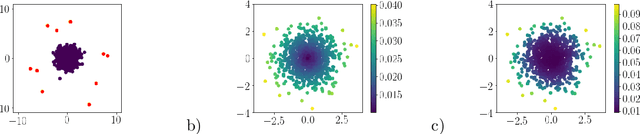
When one is faced with a dataset too large to be used all at once, an obvious solution is to retain only part of it. In practice this takes a wide variety of different forms, but among them "coresets" are especially appealing. A coreset is a (small) weighted sample of the original data that comes with a guarantee: that a cost function can be evaluated on the smaller set instead of the larger one, with low relative error. For some classes of problems, and via a careful choice of sampling distribution, iid random sampling has turned to be one of the most successful methods to build coresets efficiently. However, independent samples are sometimes overly redundant, and one could hope that enforcing diversity would lead to better performance. The difficulty lies in proving coreset properties in non-iid samples. We show that the coreset property holds for samples formed with determinantal point processes (DPP). DPPs are interesting because they are a rare example of repulsive point processes with tractable theoretical properties, enabling us to construct general coreset theorems. We apply our results to the $k$-means problem, and give empirical evidence of the superior performance of DPP samples over state of the art methods.

Optimized Algorithms to Sample Determinantal Point Processes

In this technical report, we discuss several sampling algorithms for Determinantal Point Processes (DPP). DPPs have recently gained a broad interest in the machine learning and statistics literature as random point processes with negative correlation, i.e., ones that can generate a "diverse" sample from a set of items. They are parametrized by a matrix $\mathbf{L}$, called $L$-ensemble, that encodes the correlations between items. The standard sampling algorithm is separated in three phases: 1/~eigendecomposition of $\mathbf{L}$, 2/~an eigenvector sampling phase where $\mathbf{L}$'s eigenvectors are sampled independently via a Bernoulli variable parametrized by their associated eigenvalue, 3/~a Gram-Schmidt-type orthogonalisation procedure of the sampled eigenvectors. In a naive implementation, the computational cost of the third step is on average $\mathcal{O}(N\mu^3)$ where $\mu$ is the average number of samples of the DPP. We give an algorithm which runs in $\mathcal{O}(N\mu^2)$ and is extremely simple to implement. If memory is a constraint, we also describe a dual variant with reduced memory costs. In addition, we discuss implementation details often missing in the literature.

Échantillonnage de signaux sur graphes via des processus déterminantaux

We consider the problem of sampling k-bandlimited graph signals, ie, linear combinations of the first k graph Fourier modes. We know that a set of k nodes embedding all k-bandlimited signals always exists, thereby enabling their perfect reconstruction after sampling. Unfortunately, to exhibit such a set, one needs to partially diagonalize the graph Laplacian, which becomes prohibitive at large scale. We propose a novel strategy based on determinantal point processes that side-steps partial diagonalisation and enables reconstruction with only O(k) samples. While doing so, we exhibit a new general algorithm to sample determinantal process, faster than the state-of-the-art algorithm by an order k.